л58. Философия нечетких множеств
Когда речь идет о философии каких-то объектов,
то нигде не рассматривается их философия ради их философии. Дело в том, что
философия предшествует созданию объекта, а не является следствием из него.
Философия есть средство, способ, механизм эволюционного развития знания и
заключается в том, как изменить существующий объект, чтобы получить возможность
перейти к новому объекту. Философия строит мост перехода от известного к
неизвестному. Исходным пунктом всего нового является идея. Нет идеи - нет и её
реализации. Циолковского называют отцом космонавтики потому, что он выдвинул
идею реактивного летательного аппарата. Поскольку идея выдвинута, идет её
разработка, создаются соответствующие объекты. Но всё это уже дело техники.
Т.о., идея создает реальность, и задача состоит в том, чтобы идея была высказана
т.о., чтобы она стала удобоваримой для современников.
Заде пишет: " На
практике во многих случаях принятие решений происходит в таких условиях, когда
цели, ограничения и последствия возможных действий точно не известны. Для
обращения с неточно известными величинами обычно применяется аппарат теории
вероятностей, а также методы теории принятия решений, теории управления и теории
информации. Таким образом, интуитивно принимается допущение, что неточность
(imprecision) независимо от ее природы может быть отожде-ставлена со
случайностью (randomness). Это, как нам представляется, является спорным
предположением.
По нашему убеждению, необходимо различать случайность (randomness) и
расплывчатость (fuzziness), причем последняя является основным источником
неточности во многих процессах принятия решений. Под расплывчатостью
подразумевается тот тип неточности, который связан с расплывчатыми множествами2)
[20, 21], т. е. с классами, в которых нельзя указать резкую границу, отделяющую
элементы, принадлежащие к данному классу, и элементы, не принадлежащие к нему.
Например, класс зеленых предметов есть расплывчатое множество. Расплывчатыми
являются также классы объектов, характеризуемых такими часто используемыми
прилагательными, как «большой», «маленький», «существенный», «значительный»,
«важный», «серьезный», «простой», «точный», «приближенный» и т. п. Фактически
большинство классов в реаль-ном мире, в противоположность понятию класса или
множества в математике, не имеют четких границ, которые отделяли бы входящие в
класс объекты от объектов, не входящих в него. В связи с этим важно отметить,
что в разговоре между людьми расплывчатые утверждения, такие, как: «Джон на
несколько дюймов выше Джима», «х значительно больше у", «У корпорации X
прекрасные перспективы», «На фондовой бирже наблюдается резкий спад», все же
несут значительную информацию, несмотря на неточность выделенных курсивом слов.
Более того, на наш взгляд одно из основных различий между человеческим
интеллектом и «искусственным интеллектом» ЭВМ заключается в том, что в отличие
от современных компьютеров люди обладают способностью оперировать расплывчатыми
понятиями и выполнять расплывчатые инструкции.
В чем состоит различие
между случайностью и расплывчатостью? По сути дела, случайность связана с
неопределенностью, касающейся принадлежности или непринадлежности некоторого
объекта к нерас-плывчатому множеству. Понятие же расплывчатости относится к
классам, в которых могут иметься различные градации степени принадлежности,
промежуточные между полной принадлежностью и непринадлежностью объектов к
данному классу. Например, расплывчатое утверждение «Корпорация Х придерживается
прогрессивных взглядов» является неточным вследствие расплывчатости выражения
«прогрессивные взгляды». В то же время утверждение- «Вероятность того, что
корпорация X работает в убыток, равна 0,8» содержит информацию о мере
неопределенности относительно принадлежности корпорации X к нерасплывчатому
классу корпораций, работающих в убыток. Аналогично утверждение «Степень
принадлежности Джона к классу высоких мужчин равна 0,7» является
«невероятностным» утверждением относительно принадлежности Джона к расплывчатому
классу высоких мужчин, а утверждение «Вероятность того, что Джон женится в
течение года, равна 0,7»—«вероятностное» утверждение, характеризующее
неопределенность наступления нерасплывчатого события (женитьбы).
Это различие приводит к тому, что математические методы теории расплывчатых
множеств совершенно не похожи на методы теории вероятностей. Они во многих
отношениях проще вследствие того, что понятию вероятностной меры в теории
вероятностей соответствует более простое понятие функции принадлежности в теории
расплывчатых множеств. Кроме того, вместо обычных операций а + b и ab, где а и b
— действительные числа, используются более простые операции Мах (a, b) и Min(a,
b). По этой причине даже в тех случаях, когда расплывчатость в процессе принятия
решений может быть представлена вероятностной моделью, обычно удобнее
оперировать с ней методами теории расплывчатых множеств без привлечения аппарата
теории вероятностей.
Процессы принятия решений, в которых тем или иным
образом присутствует расплывчатость, могут изучаться с различных точек зрения
[22, 9, 14]. В настоящей статье основное внимание уделяется введению трех
фундаментальных понятий — расплывчатой цели, расплывчатого ограничения и
расплывчатого решения, а также исследованию их применения к многошаговым
процессам принятия решений, в которых цели или ограничения могут быть
расплывчатыми, а управляемая система может быть либо детерминированной, либо
стохастической, но не расплывчатой. Это, однако, не накладывает существенных
ограничений на применимость концепций и методов, описанных в последующих
разделах.
Вообще говоря, под расплывчатой целью подразумевается цель,
которую можно описать как расплывчатое множество в соответствующем пространстве.
Так, простым примером расплывчатой цели, связанной с вещественной переменной х,
может служит цель: «х должно быть существенно больше 100». Со своей стороны,
ограничение «х должно находиться приблизительно в интервале 20—25» является
простейшим примером расплывчатого ограничения. Источниками расплывчатости в этих
утверждениях являются слова, выделенные курсивом. Менее тривиальным примером
может служить детерминированная система, работающая в дискретном времени и
описываемая уравнениями состояния п = 0, 1, 2, .... где хn
и un
обозначают соответственно переменную состояния и входную переменную в момент
времени n и для простоты предполагаются вещественно-значны-ми. Расплывчатое
ограничение, наложенное на входную переменную, могло бы здесь иметь вид
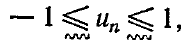
|
|
|