Персональный сайт Валерия Штырова

Воспринимать нужно не слова, а понятия. Понятие же воспринято тогда, когда можешь выразить его другими словами. Ты прочитал, и что-то понял. Когда ты высказываешь своими словами, ты показываешь, что именно из прочитанного ты понял

Метод математической индукции

Если бы мне случайно не попалась книга И.С.Сломинского
"Метод математической индукции", я бы, пожалуй, до конца жизни так и не понял, что это такое.
   "Утверждение справедливо для всякого натурального n, если: 1) оно справедливо для n = 1 и 2) из справедливости утверждения для какого-либо произвольного натурального n = k следует его справедливость для n = k+1"

   Обобщение: если между объектами установлен определенный порядок, такой, что для всякого объекта можно определить предшествующий ему и следующий за ним ( что позволяет объекты индексировать натуральным рядом чисел), и если известно, что если предшествующий элемент обладает некоторым свойством, то им обладает и последующий элемент, то если первый элемент обладает некоторым свойством, то им обладают все элементы.

   Вопрос, следовательно, заключается в том, как доказать передачу свойства от предыдущего к последующему.
   При этом переход к последующему должен порождаться из предыдущего. Так, например, всякое последующее число натурального ряда порождается из предыдущего прибавлением к нему единицы.

  " Доказательство. Предположим противное, т. е. предположим, что утверждение справедливо не для всякого натурального п. Тогда существует такое натуральное т, что 1) утверждение для п = т несправедливо, 2) для всякого п, меньшего m, утверждение справедливо (иными словами, т есть первое натуральное число, для которого утверждение несправедливо). Очевидно, что m>1, так как для п=1 утверждение справедливо (условие 1). Следовательно, т— 1 — натуральное число. Выходит, что для натурального числа m—1 утверждение справедливо, а для следующего натурального числа т оно несправедливо. Это противоречит условию 2."

   Обратим внимание на структуру доказательтва, которая исходит из тавтологии "если р, то р", ( р=р ) и закона противоречия "р и не-р = ложь. Поэтому если сталкиваемся с противоречием, то на основе закона исключенного третьего, зная, что одно из утверждений ложно, мы можем утверждать, что другое истинно. Одна из сторон противоположности принимается в качестве критерия истины, то есть рассматривается как безусловно истинная, и истинность другой стороны определяется через её отношение к первой. Вначае мы имеем формулировку р, выступающую в качестве критерия и выступающую в качестве определения математической индукции. Это определение состоит из двух положений: положение 1. истинность высказывания относительно первого объекта. Положение второе: из истинности высказывания относительно предыдущего объекта следует истинность этого же высказывания относительно последующего. Это что-то в роде завершенной бесконечности, понятия. Вторая часть, собственно доказательство, представляет собой уже переход к практике, к чувственной реальности. Делается утверждение относительно следствия, а именно, предполагается, что истинностное значение произвольного элемента является не истинным, а ложным. Но тогда ложным должен быть предшествующий элемент на основании закона контрапозиции: из того, что из р следует q, следует, что из не-q следует не-р: p→q,не-q ; следовательно, не-р.Вторая часть закона контрапозиции связана с первой только логическими законами и ничего не привносит в первую в содержательном отношении. Здесь доказывается всего лишь логическая непротиворечивость. Мы допустили ложность следствия, и прошли от произвольного элемента через все предыдущие к первому элементу и получили противоречие с ним. И из этого противоречия делаем вывод о неверности предположения о ложности следствия. Единственное, что мы получаем из этой тавтологии - это переход от того, что придумано, к чувственной и опять - таки придуманной сфере. Мы не выходим за пределы головы. В этом заключаются все доказательства математики: в высказывании ею общих положений, используемых для последующего применения их к отдельностям.

   Но для того, чтобы подобный подход мог работать, должны быть созданы формализмы, ибо он может работать только на формализмах.
   Именно поэтому также и рассчитываемые в математике реалии вначале формализуются, затем формализмы рассчитываются и затем осуществляется деформализация.

   Пример. Вычислить сумму: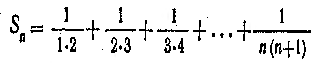

Сумма начальных членов

Можем предположить, что сумма S_n=n/(n+1) Посмотрим, что нам даст метод математической индукции. Первый член соответствует предполагаемой формуле, сл., первое условие матиндукции выполняется. Посмотрим, выполняется ли второе условие. Нужно показать, что если формула верна для к-ого члена, то она будет верна и для к+1 члена, то есть если выполняется к/(к+1), то выполнится и для (к+1)/(к+2)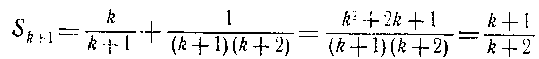

Т.о., если мы предположим, что произвольный предыдущий член выполняет формулу и её выполняет и последующий член, то наше предположение оказалось верно.

При доказательстве формулы uu_k=2k-1 нечетного числа как функции от его номера в ряду нечетных чисел мы начинаем с определения того, чему должно быть равно, согласно этой формуле, к+1 число:
u_k+1=2(k+1)-1=2k+1. Т.о., ответ нам уже дан, а теперь нам нужно придти к этому ответу, то есть мы должны взять предшествующее число, и посмотреть, посредством какой операции оно должно дать нам следующее число. То есть нам нужно знать, как, каким образом, в соответствии с каким правилом мы можем от предыдущего числа перейти к последующему. Если мы знаем предыдущее нечетное число, то мы знаем также, что четные и нечетные числа чередуются, поэтому к предыдущему числу нужно прибавить 2, и мы получим последующее. Значит, u_k+1=2k-1+2=2k+1. Т.о., в математической индукции есть важная вещь: для определния закона перехода мы не гадаем на кофейной гуще, но обращаемся к чувственной достоверности, хотя она и является идеальным построением человеческой головы.

Допустим, мы хотим найти формулу суммы S_nпервых n нечетных чисел. Для этого напишем следующую таблицу:

n 1 2 3 4 5 6 7 8
u_n 1 3 5 7 9 11 13 15
S_n 1 4 9 16 25 36 49 644

Из рассмотрения таблицы приходим к гипотезе S_n=n² . На основании формулы получаем её значение для n+1 нечетных чисел: S_n+1=(n+1)² =n² + 2n + 1.
    Следует особо указать на важнейшую роль применения формул как всеобщей структуры. Благодаря формуле мы имеем дело с общим, а не отдельным.
   Итак, теперь мы знаем, какое выражение должны получить в результате прибавления к сумме S_n следующего за ним числа. Но мы при этом должны знать само это число u_n+1 Получаем: u_n+1=2(n+1)-1=2n+1. Отсюда: S_n+1 = S_n +u_n+1 = n² + 2n+1 ч.т.д.

   Задача 1. Найти u_n, если u₁=1 и u_k = u_k-1+3
   Точно также, как врачу важно поставить правильный диагноз прежде, чем приступать к лечению больного, точно также важно правильно понять задачу прежде, чем приступать к её решению.
   Нам дано значение первого члена (база (1`) и дана связь последующего и предыдущего членов последовательности чисел (индуктивная часть 2`). По ним определяем первые члены последовательности:

u₁=1
u₂=1+3=4
u₃=4+3=7
u₄=7+3=10
u₅=10+3=13
u₆=13+3=16
u₇=16+3=19
.........
u_k=u_k-1+3

В первом члене последовательности число 3 содержится ноль раз (0*3), во втором один раз (1*3), в третьем два раза (2*3), в четвертом три раза (3*3) и т.д., следовательно, для каждого n-ого члена берется (n-1)3 и к полученному числу добавляется единица. Т. о. получаем гипотезу: u_n= 3(n-1)+1= 3n-3+1=3n-2. Проверяем: 1). Базис (1`): u_k+1=u_k+3=3к-2+3=3к+1 2). Индукция (2`): u_k+1=3(к+1)-2=3к+1. Т.о., 3к+1=3к+1. К+1 член, определенный разными способами, имеет одно и то же значение. В данном случае закон тождества выступает в качестве механизма проверки истинности выдвинутой гипотезы.

Задача 2. Найти сумму
S_n=2⁰+2¹+2²+2ⁿ+...+2ⁿ

             1   2   3 4   5 6
       u_n=2⁰ 2¹ 2² 2³ 2⁴ 2⁵
      Sⁿ=1 3 7 15 31 63
S_n+1-S_n=2 4 8 16 32 64

   S_n+1-S_n=2ⁿ. (1`): u_n=2^n-1, S_n=2ⁿ-1 ; (2`): S_n+1=S_n+u_n+1=2ⁿ-1+2ⁿ=2*2ⁿ-1; S_n+1=2ⁿ⁺¹-1=2*2ⁿ-1 Т.о. S_n+u_n+1=S_n+1, ч.т.д.

   Задача 3 Найти сумму первых n членов натурального ряда
   Строим таблицу:

          n 1 2 3    4    5    6    7    8    9
        S_n 1 3 6 10 15 21 28 36 45
S_n+1-S_n 2   3 4   5    6    7     8    9
                1   1 1    1    1    1     1

Из таблицы, обобщая, получаем: S_n+1-S_n=n+1. S_n=n(n+1)/2. Тогда S_n+1=(n+1)(n+2)/2. (a) 2) 2`: Из таблицы, обобщая, получаем: S_n+1=S_n+(n+1)=n(n+1)/2+(n+1)=(n+1)(n+2)/2 (b). (a)=(b), ч.т.д.

Задача 4. Найти сумму квадратов первых членов натурального ряда
Строим таблицу:

               n 1    2     3        4      5      6         7          8
              n² 1    4     9      16    25    36       49        64     n²-(n-1)²=2n-1=D
              D    3     5     7       9      11     13      15            D_n-D_n-1 =2
             S_n 1    5    14     30    55     91     140      204   S_n=S_n-1+n²
    S_n-S_n-1 4     9    16    25    36      49       64          S_n-S_n-1=n² =A_n+1
A_n-A_n-1          5      7      9     11     13        15              A_n-A_n-1=2n+1=B_n
  B_n+1-B_n             2      2      2       2         2                    B_n-B_n-1=2=C

Метод последовательного обобщения
Пусть дан натуральный ряд чисел и нужно найти сумму его первых n членов. Применим метод последовательного обобщения, начиная с первого члена, затем первого и второго, затем первого, второго и третьего и т.д. до тех пор, пока формула не будет выполняться для всех n.
n 1 2 3 4 5 6 7
S_n1 3 6 10 15 21 28
. Для члена 1 берем n. Для первых двух членов получаем n(n+1)/2. Эта формула выполняется и для всех членов. Заметим, что разность между суммами представляет собой натуральный ряд чисел, начиная с двух, и, соответственно, разность их постоянна

Применяем метод последовательного обобщения.
   n=1[1] →n; n=2 [5] → n(n+3)/2 ; S_n=1,2=n(n²+1)/2; S_{n=3 [14]}= (n³+1)/2 ;S_{n=1,2,3
[1,5,14] =?}
   Tеперь нам нужно обобщить полученные формулы. S_n=1,2=n(n²+1)/2=n³/2+n/2 и S_{n=3 [14]}= (n³+1)/2=n³/2+1/2 Обобщение может заключаться в том, что знаменатели выражений мы заменим буквами, обозначающими постоянные. кроме того, глубина разностей в таблице равна 3. Поэтому целесообразно ввести общую форму: n³/a + n²/b+n¹/c =А+В+С Теперь нам нужно определить значения a,b,c т.о., чтобы они удовлетворяли значениям n=1,2,3. Пусть n=1. Тогда в числителях всех дробей мы получим 1, и сумма числителей должна быть равная наибольшему общему делителю. Первым из таких возможных делителей является число 6. Тогда дроби будут содержать в знаменателе числа 2,3,6. Для n=1 неважно, какой из дробей они будут приписаны. Затем нам нужно определиться с конкретикой приписывания чисел знаменателям дробей. Пусть n=5. Прикинем величины чисел в зависимости от того, какие знаменатели мы припишем дробям. Если мы припишем знаменателю дроби А число 6, дроби В число 3 и дроби С число 2, то получим минимальное число 8/6+4/3+2/2<5. Возьмём максимально возможное число при знаменателе А=2, В=3, С=6, получим 4+1+1/3 >5. Уменьшим число, приписав знаменателю А число 3, В - 2. Получим: 8/3+4/2+2/6=(16+12+2)/6=5. Т.о получили: a=3, b=2, c=6. Проверим полученную формулу при n=3. Осуществив подстановки в формулу, получаем число 14. Следовательно, обобщение на три первых элемента выполнено правильно. Проверим формулу на следующем n=4. Мы должны получить число 30. Делаем подстановки в формулу и получаем число 30. Итак, мы получили формулу: n³/3 + n²/2+n¹/6. (1) Теперь мы можем считать, что гипотеза нами сформулирована, и нам следует её проверить индукцией.

   Начнем с того, что избавимся от показателей степени больше 1 при n. Для этой цели приведем формулу (1) к общему знаменателю и осуществим преобразование числителя в соответствии со следующим приёмом. Из выражения (a+b)(c+d)=ac+ad+bc+bd мы видим, что его правая часть состоит из четырех членов, причем, попарно два его члена имеют одинаковые буквы, и в каждой паре одинаковые буквы связывают сумму одинаковых частей. Т.о.: ac+ad+bc+bd=a(c+d)+b(c+d)=(a+b)(c+d). Поэтому, если мы имеем какую-то сумму, то можем рассмотреть её с этой точки зрения и соответствующим образом преобразовать. И, разумеется, посредством обратной проверки мы всегда можем установить правильность произведенной операции.
    n³/3 + n²/2+n¹/6=(2n³ + 3n²+n¹)/6. 2n3 + 3n2+n1=2nn² + n²+2n²+n¹=(n²+n)(2n+1)=n(n+1)(2n+1). Получили: n(n+1)(2n+1)/6 (2) Из (2) для n+1 получаем: (n+1)(n+2)(2n+3)/6 (4)
   Индуктивный шаг (2): S_n+1=S_n+n²=n(n+1)(2n+1)/6+(n+1)² (5). Покажем, что (4)=(5), то есть что (n+1)(n+2)(2n+3)/6=n(n+1)(2n+1)/6+(n+1)^2. Сократим обе части уравнения на n+1, перемножим сомножители обеих частей и приведем подобные члены. Получим: 2n² + 7n+6, ч.т.д.
   Обратим внимание вот на что: уравнение (5) позволяет выявить генез преобразования правой части уравнения к левой. Именно: n(n+1)(2n+1)/6 +(n+1)²=((n+1)/6)(n(2n+1)+6(n+1))=((n+1)/6)(2n²+7n+6)=((n+1)/6)(2n²+3n+4n+6)=((n+1)/6)(n(2n+3)+2(2n+3))=((n+1)/6)(n+2)(2n+3)) (6). (6)=(4), ч.т.д.

   13.10.09 г.