Логика и реальность

 Диагональ квадрата

назад Из всех прямоугольников только квадрат имеет диагональ, которая проходит через все точки и число её точек равна числу точек катета .
    -Квадрат диагоналями может быть разделен как на две части, так и на четыре, поскольку имеет две диагонали, каждая из которых всё это делит пополам, при этом одна точка является точкой пересечения двух диагоналей. В целом же квадрат может делится на разное число частей. Но в настоящем случае рассмотрим только деление квадрата на 2.

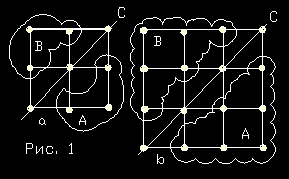
   -Пусть n=3, тогда n²=9 (Рис.1а)
  
   -Берем формулу суммы первых n чисел натурального ряда n(n+1)/2.
    Пусть n=3,  n²=9. Тогда мы имеем квадрат рис. 1а. Возникает вопрос: как мы можем разделить его на две части. Квадрат рис.1а состоит из зон А и В по три независимых элемента, и зоны С, общей обеим половинам квадрата. Дело, в частности, может быть представлено таким образом, что линия зоны С делит все элементы диагонали пополам. Тогда на каждую из половинных частей единиц получим по полторы единицы, и всего в результате деления получаем по 4,5 элементов. Впрочем, подобный подход относится к "изврату", а не к сущности дела: нам просто нужно число элементов диагонали квадрата, который, может быть, следовало бы назвать точечным или натуральным квадратом, поскольку предполагается, что он содержит только натуральные объекты, то есть какие-то единичности, разделить на два. Но сумма первых трех элементов равна шести. Значит, для каждой из полученных половин  не хватает по полтора элемента. Но если мы делим на два, а потом оказывается, что у нас как раз половины и не хватает, то это означает, то мы должны зону С брать два раза. А взять зону С два раза - это значит к квадрату добавить катет, ведь он равен диагонали. . Т.о. мы переходим к формуле (n²+n)/2. В этой формуле n выступает в качестве средства удвоения диагонали. И это - правило удвоения элементов, которые находятся на диагонали, является общим.
   -Как можно видеть из рис. деление квадрата элементов может осуществляться "по частным "диагоналям. Во всех этих случая перегиб квадрата по диагонали дает общие  точки, которые, для адекватного деления, должны быть удвоены, что и достигается дополнительным n. Но то, что названо частной диагональю, под которой подразумеваются  симметричные друг другу точки  относительно основной диагонали, которые совмещаются при перегибе квадрата по диагонали, при этом получающиеся в результате совмещения угловые точки могут рассматриваться как вырожденные частные диагонали, это вопрос для особого рассмотрения.
   -Отличие квадрата четного числа от нечетного состоит в том, что квадрат нечетного числа содержит одну точку, которая делится диагональю на две половины, а у квадратов четных чисел этого нет.
    Пусть n=4, n²=6.После деления квадрата на два мы получили по 8 элементов в каждом, то есть каждой из частей полученных частей не хватает по два элемента, которые получаются введением n/2 для каждой из частей. Связь, которая здесь имеет место, состоит в том,  что число элементов диагонали равна числу элементов катета квадрата. Так как мы делим на два,  то число элементов диагонали и, соответственно, катета также делится на 2, и поэтому для каждой из сторон противоположности не хватает по половине. Результат всякого деления на два состоит в том, что мы получаем две половины, но одна половина у нас оказывается снятой, другая - положенной. И поэтому, разделив  число элементов катета на два, мы получаем одну половину, которую мы выбрали и которая потому для нас выступает в качестве положенной, и другую половину, которая снята и которая неявно добавляется к снятой половине. Число элементов диагонали может быть четным и нечетным. В случае нечетного числа элементов один элемент делится на две части, и мы получаем для каждой стороны противоположности по половинке. Деление n на два даём нам как недостающие целые, так и недостающие половинки элементов.


   Обратим внимание на рис.2a,b На обоих рисунках  задаёмся одним и тем же вопросом: что произойдет, если  удалим из квадрата диагональ. Рисунки показывают, что в результате от квадрата n мы переходим к квадрату (n-1)Но самое важное заключается в том, что во вновь полученном квадрате мы снова получаем диагональ со совмещенными точками. Т.о., любой квадрат образуется множеством точек двух  равнобедренных прямоугольных треугольников путем совмещения их гипотенуз.

   Отмечу любопытную "ошибку", связанную с диалектикой мысли. Всюду выше, говоря о квадрате и его диагонали,  вместо термина "сторона квадрата" употреблялся термин "катет", который принадлежит прямоугольным треугольникам и обозначает стороны, прилежащие к прямому углу. В квадрате неявно присутствует треугольник в рассматриваемом  аспекте. И этот природный, непроизвольный способ мышления представляет собой способ видеть одно в другом, и всюду, не только в математике, где мы наблюдаем непроизвольное называние одних объектов другими объектами, имеет место связь этих объектов, свечение одних объектов в других, свечение, которое превращает разные объекты в один объект и переносит свойства одного объекта на свойства другого.. Мы говорим "катет" в приложении к квадрату, и, значит, уже неявно выделили в квадрате прямоугольный треугольник, и в диагонали квадрата увидели его гипотенузу. Т.о., говоря об одном, говорим о другом (предполагаем другое)и, тем не менее, речь шла всё-таки о квадратах.