Логика и реальностьОбъкты и имена (математическое
мышление)
Принцип математического мышления состоит в том, что
математик оперирует объектами, которые принадлежат чувственной сфере,
которую он сам создает. Имена объектов чувственной сферы выполняют функцию
указателей на соответствующие объекты и представляют собой перевод
чувственной сферы в рациональной в речевой форме.
Упорядоченное множество
объект & ; имя: и
объект → ; имя: "если...то..."
Объекты x,y,z; имя: – неопределенный (любой) элемент
множества
Объект А; имя: множество
Объект: ≤; имя: отношение порядка
объект: х≤х; имя: рефлексивность
объект х≤у & y≤x→x=y; имя: антисимметричность
объект х≤у & y≤z→x ≤z; имя: транзитивность
свойства объекта (≤) =(( х≤х )+( х≤у & y≤x→x=y)+( х≤у & y≤z→x ≤z))
Соответственно, если даны объекты А, В, С такие, что А= х≤х, В= х≤у &
y≤x→x=y, С = х≤у & y≤z→x ≤z, то получим объект ≤ = (А,В,С)
утверждение: отношение порядка между элементами х,у выполняется, если они
подчинены законам рефлексивности, антисимметричности и транзитивности
p.s. Сравним два
объекта: (≤) =(( х≤х )+( х≤у & y≤x→x=y)+( х≤у & y≤z→x ≤z)) и ≤ = (А,В,С)
Восприятие первого объекта соответствует чувственному восприятию и,
соответственно, чувственному отношению. Здесь объект представляет сам себя.
Восприятие частей А,В,С второго объекта уже предполагает мышление, так как
эти части представляют не себя, а другие объекты и тем самым уже
представляют собой объекты-имена.
Мозгом выделяется объект
- как одно, часть объекта снова выделяется как объект и как одно, свойство
выделяется как одно и т.д. Мозг оперирует единицами. Поэтому: объекты А,В,С
=Е. Откуда ≤=Е, и мы получили выражение закона тождества как отношение
между чувственностью и словом и как выражение связи между полушариями
большого мозга. От объекта переходим к его выражению в слове Е, затем идет
операция дифференцирования Е=А,В,С, и мы получили части объекта, к которым и
переходим: А= х≤х, В= х≤у & y≤x→x=y, С = х≤у & y≤z→x ≤z точно также,
как в процессе формирования Е мы применяли противоположную операцию -
интегрирования одного из множества одних как его частей.
объект {A, ≤} ; имя: упорядоченное множество А.
Определение минимального и максимального элементов упорядоченного множества
Объекты а, b, c –
имя: определенные элементы множества, могут
применяться с нижними индексами.
Объекты: amin , amax
; имя: минимальный, максимальный элемент
множества A.
Свойство объекта: (а=amin)=а ≤х &
a≠x; (а=amax
)= x≤a & a≠x, где а,х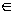 А А
Смысл понятия "неопределенный элемент" - это значит любой элемент
из множества А. Поэтому применение неопределенного элемента означает
утверждение, что речь идет обо всех элементах множества А. Т.о. за
неопределенным элементом стоит призрак квантора всеобщности.
Утверждение: Элемент а упорядоченного множества А является минимальным
(максимальным), если он меньше (больше) или равен любому другому элементу
множества А
Элемент - это объект. Когда мы говорим: больший, меньший - это
количественная характеристика свойства объекта, с которым объект
отождествляется (который представяет объект). Например, когда мы говорим
человек, мы обознаем объект. Но если мы в количественном отношении различаем
людей по весу, росту или возрасту, то все люди распределятся по
соответствующим количественным шкалам, так что мы сможем говорить о
множестве людей, о подмножестве минимальных и максимальных элементах
этого множества
Верхняя и нижняя границы упорядоченного множества.
Объект: < ={a, <} имя Знак < , примененный к объектам,
обозначает «меньше» аналогично для других знаков этого рода.
<={A, <} имя: Знак <, примененный к множествам, обозначает также
отношения включения множества во множество.
Объект:
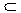 ; имя: отношение включения класса в
класс ; имя: отношение включения класса в
класс
объект: А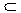 В имя: множество А
включено в множество В В имя: множество А
включено в множество В
Объект: S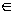 А&S≠0 имя:
непустое множество S включено в множество А А&S≠0 имя:
непустое множество S включено в множество А
Целью создаваемого параллелизма является
формирование привычки оперировать с математическими объектами как с
чувственными, а не словесными объектами
объект: а0: имя верхняя
(нижняя) граница множества S
объект: а0=а≤а0(а0=а0≤а)
имя: а0
Непроизвольно
происходит отождествление объекта и имени, что связано со стремлением
упрощения связи миров чувственности и слова, что приводит к единому
пространству объектов и их имён, которое в довольно явной форме мы встречаем
у Аристотеля. Получаем:
а0 = а0.
Получено тождество объекта и имени. Один и тот же образ в математике может
применяться то как объект, то как имя, каковой способ употребления
определяется контекстом. Но обычно мы имеем дело с параллелизмом того и
другого. Говоря: "а0 есть верхняя или
нижняя граница множества А, мы употребляем имена а0
и А, имея ввиду объекты а0 и А, то есть мы
высказываемся не об именах а0 и А, а об их
объектах. Это совершенно то же самое, с чем мы сталкиваемся в условных
рефлексах, где условный раздражитель выступает в качестве представителя
безусловного. Только если в условном рефлексе положенной, движущей стороной
процесса является безусловный, то в мышлении положенной является речь,
которой предполагается объект. Объект, т.о., дается не непосредственно, а
опосредованно, он "светится" в речи. Человек видит объект через призму
(фильтр) речи.
О кванторах общности и существования.
Когда мы говорим: "Человек есть животное", мы имеем ввиду отдельного
человека. Так как в чувственной сфере мы употребляем термин "человек"
относительно отдельного человека, но один отдельный человек не отличается от
другого отдельного человека, то предикат "животное" применяется ко всем
людям. Но мы не можем сказать, что человек есть учитель (по профессии), так
как быть учителем свойственно не всем людям. Правильно будет сказать, что
учитель есть человек. Мы на практике не говорим, что некоторые люди являются
учителями. Т.о. получаем, что квантор существования есть производный
квантор, получаемый в результате обращения суждения. В естественном языке
существует вектор высказываний, заключающийся в том, что непосредственно
высказывают общее о частном, но не частное об общем. Высказывание частного
об общем есть вывод из высказывания общего о частном. Какова практика в этом
отношении? Допустим, мы установили, что какой-то предмет обладает некоторым
свойством. Но если в чувственной сфере мы имеем дело с отдельными
предметами, то в сфере мышления мы имеем дело с идеями предметов, а всякая
идея носит всеобщий характер. Для неё отдельный предмет - экземпляр,
представитель идеи. Поэтому в сфере мышления единичные предметы обозначаются
посредством общих понятий. Для мыслительного аспекта языка все объекты суть
какое-то общее понятие. С другой стороны, также, имея ввиду на уровне мысли
понятие человека, на уровне чувства мы соотносим это понятие с отдельным
абстрактным человеком, то есть с соответствующим образом отдельности,
хотя этот образ и может быть достаточно безобразен, будучи представлен в
виде малоопределяемого ощущения.
Точная верхняя (нижняя)
граница множества.
Объект:
at={аt=а0}&t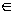 T=Nа0
имя: индексированное множество элементов верхней или
нижней границы
подмножества упорядоченного множества T=Nа0
имя: индексированное множество элементов верхней или
нижней границы
подмножества упорядоченного множества
Объект: sup at
(inf at)= at
>at -аt
имя:
В множестве А мы можем выделить подмножество S. Мы можем
сделать это, выбирая объекты случайным образом, но можем это сделать,
выбирая связные объекты. Вообще, что значит упорядочить множество в
соответствии с данными правилами? Это значит найти место каждому из
элементов в некоторой линейно-параллельной последовательности. У нас
найдется в общем случае множество элементов, равных друг другу, тогда они
займут одно место: ни один из них не будет впереди или позади, раньше или
позже другого. В остальном же они образуют последовательный ряд. Если в этом
ряду мы выделим определенный интервал объектов, то мы получим, конечно,
некоторую верхнюю и нижнюю границу. При этом на границе может оказаться один
или множество одинаковых элементов.
Принцип индексирования
элементов множества Действительно, правило индексации элементов
множества должно быть задано явно. Должен существовать процесс, реализующий
это правило. Например, речь может идти о случайной выборке. Тогда
естественно задать вопрос по поводу технологии её осуществления. Кажется
естественным, что выбранный элемент не возвращается в множество. Выбрали
первый элемент, присвоили ему индекс 1, второй элемент - индекс два, и т.д.,
наконец, n-ый элемент - индекс n. И т.о. каждый из элементов множества
получает своё собственное имя, и мы получаем возможность иметь дело с
индивидуальностями. И тогда получаем объекты
a={a}=A;
NA=NT=n (NA - число
элементов множества А(мощность множества А)) t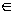 T;
at индексированные элементы
множества А, где множество Т представляет собой интервал из
натурального ряда чисел 1, 2, ..., n T;
at индексированные элементы
множества А, где множество Т представляет собой интервал из
натурального ряда чисел 1, 2, ..., n
Выборка
элементов может делаться в соответствии со значениями параметров. Если
выборка делается по одному параметру, то как может выглядеть процесс
индексации? выбрали один элемент, получили его значение. присвоили ему
индекс 0. Выбрали второй. Он будет больше или меньше выбранного, или равен
ему. Соответственно, обозначаем его ка 0+1, 0-1 или 0. Следующая выборка
даст элемент равный, меньший или больший 0, -1, +1 или же его
количественный признак будет находитсья между признаками объектов 0, -1 или
+1 Тогда, соответственно, делим интервал 0,+/-1 на два. Получаем индекс для
объекта +/-0,5. И т.д. После того, как мы выбрали все элементы, мы получили
их индексацию, посредством которой все элементы оказались упорядочены,
причем, в некоторых случаях получены элементы с одинаковыми индексами. Т.о.
получено множество подмножеств множества А, содержащих по одному или
несколько элементов. Разумеется, в свою очередь мы можем осуществить
дополнительную индексацию элементов подмножеств, содержащих несколько
элементов. Во всяком случае, все подмножества у нас с индексами, и они
располагаются в конечную линейную последовательность. Теперь можем
подмножеству с элементом(ами) с минимальным индексом присвоить новый индекс,
равный единице, и подобным же образом следующему за ним и т.д. и т.о.
осуществить переиндексацию элементов в приемлемую форму.
|

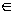 А
А
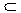 ; имя: отношение включения класса в
класс
; имя: отношение включения класса в
класс