Логика и реальность Точки и квадраты
Карточное представление кубов натурального ряда чисел
- Рассмотрим кубы натурального ряда (рис.1)
 как
процесс. Каким образом может быть представлено всё дело. Пусть у нас
существуют квадраты натуральных чисел. Тогда, взяв соответствующее число
квадратов, получим куб. Но эти квадраты, присутствующие в кубе, могут
рассматриваться как соответствующее число карт соответствующего рода. Мы
можем также образовать из полученных наборов карт кубические объекты,
соединив соответствующие точки. При этом количество точек не изменится. как
процесс. Каким образом может быть представлено всё дело. Пусть у нас
существуют квадраты натуральных чисел. Тогда, взяв соответствующее число
квадратов, получим куб. Но эти квадраты, присутствующие в кубе, могут
рассматриваться как соответствующее число карт соответствующего рода. Мы
можем также образовать из полученных наборов карт кубические объекты,
соединив соответствующие точки. При этом количество точек не изменится.
Степени, линейность, отдельностьКогда из единиц формируется
натуральный ряд чисел, то в этом ряде оказываются также и их всевозможные
степени. При этом ни одна степень числа не говорит, что она представляет
собой что-то особенное сравнительно с остальными числами. Степени чисел
выступают в качестве таких же линейных чисел, как и все остальные.
Термин "линейные" здесь употреблен в качестве термина, различающего его от
чисел, представляющих степень. Но любое натуральное число может быть
представлено как степень единицы. И тогда род класса чисел оказывается
разделен на множество подвидов, ибо каждая очередная степень числа
представляет собой разные сравнительно с другими степенями чисел объекты. В
этом случае, к примеру, 22 представляет
объект, представленный двумя координатами, и его равенство числу четыре
представляет объекты, отличные от объектов линейного числа, равного четырём.
С каждым видом чисел оказывается связана разного рода реальность и практика
действий в ней.
Строго говоря, о числах натурального ряда как о
линейных можно говорить только в диалектическом смысле, который не полагает,
но предполагает заполненность между единицами бесконечным множеством чисел,
чем предполагается непрерывная связь между предыдущей и последующей
единицами. В метафизическом же смысле в натуральном ряде чисел мы имеем дело
с отдельностями. Другими словами, степень оказывается показателем координат
числа и тем самым качества числа, отражающего объекты со стороны их
линейных, квадратных и т.д. свойств. А к отдельности степень в её
собственном смысле не применима.
Число точек квадратов
натурального ряда, не учитывающее их смежности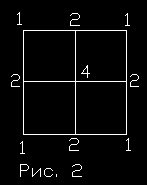 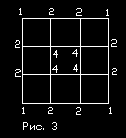 
- Мы придаем n значение 1, затем 2 и т.д. и получаем соответствующие
объекты. Любопытно то, что число точек предшествующего квадрата равно числу
квадратных плоскостей следующего квадрата. Так, 22
это 4 точки, но также и 4 плоскости в 32
Каждая квадратная плоскость содержит в себе 4 точки (рис.2) Значит, всего
имеем 16 точек.
Совмещенные (отождествленные) точки
Однако среди квадратов появляются совмещенные точки. Все
совмещенные точки представляются одной точкой. Поэтому на рис. 2
всего 8 смежных внешних внутренних точек вида 2, то есть
отождествляются две точки. Поэтому 8 неотождествленных
точек делим на 2, и получаем число 4 отождествленные
точки. Соответственно, 4 точки (типа 4) четырех смежных
квадратов делим на 4, получаем одну
отождествленную точку. И плюс у нас 4 внешние точки типа 1. Т.о.
получили число точек квадрата 4+4+1=9. А это три в квадрате.
Т.о., наши построения:
Дано число n.
Берем его квадрат: n2=L.
Находим число квадратов, соответствующих L. Согласно построению,
представленному рисунками 2-4, число строк и столбцов,
образованных квадратами, на единицу меньше числа строк и
столбцов, образованных точками, поэтому получаем число квадратов
кn=(n-1)2/
Но (n-1)2 - это квадрат точек
числа, предшествующего числу n. Следовательно, если дан квадрат
числа n, то для того, чтобы получить квадрат числа n-1,
Достаточно найти число квадратов числа n.
Например, если
число n=7, то число его квадратов равно (7-1)2=36.
С другой стороны, если нам дано число квадратов кn,
то n2=(√кn+1)2
Исходя из рассмотрения рисунков, мы можем поступить
двояко. Либо просто подсчитать "живые" точки, либо же
подсчитать "лишние" точки, =4+3=7, и вычесть их из шестнадцати,
так как всего точек в 3 в квадрате шестнадцать: 4 точки
типа 4, 4 точки типа 1 и 8 точек типа 2, всего 16 точек. Но эти
16 точек есть 4 в квадрате. Напомним, что точки типа 1 - это
точки квадрата без отождествления, то есть точки, не смежные ни
с какими другими точками, точки типа 2 - это точки, образованные
отождествлением двух смежных точек, и точки типа четыре - это
отождествленные точки, образованные четырьмя смежными точками.
Ясно, что отождествляться могут только смежные точки, то есть
такие точки, которые налагаются друг на друга.
42 =16 (рис.3) получаем фигуру
с 9 квадратами, которые содержат всего 4*9= 36 точек, что
соответствует квадрату 6. Вычитаем лишние 36-3*4-16/2=16
или отождествляем общие точки: 4+8+4=16. Мы видим, что число
внешних общих точек удваивается, а внутренних, общих всем,
учетверяется.
Приведенный пример заставляет обратить
внимание на то, что сумма неотождествленных точек числа
n, равна Nn = (n+2)2
52
показывает закономерность: все внутренние точки являются
совмещением 4 точек, внешние внутренние точки являются
совмещением двух точек, и угловые точки являются независимыми. А
это обстоятельство уже позволяет нам построить общую формулу,
которая связывает число точек квадратов n, рассматриваемых
как не совпадающие, с квадратом следующего числа той же
четности. Число внешних внутренних не отождествленных
точек равно 4(2((n-2)))=8(n-2). Число внутренних точек равно
4(n-2)2. И число независимых
точек равно 4. Получаем общее число точек квадратов для n2,
которое обозначили буквой Nn:
Nn=4 +8(n-2)+4(n-2)2=
4(n-1)2 (4) Напомним
также, что число квадратов кn
для n2 определяется по формуле:
kn=(n-1)2
(5)
Противоположность четных и нечетных чисел.
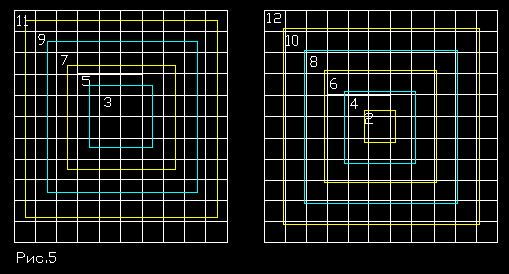
Из рисунка 5 видим, что все предшествующие квадраты оказываются включены в
последующие, однако не так, как это может показаться на первый взгляд,
согласно которому можно было бы сказать, что особенность этого процесса
заключается в том, что каждый предшествующий элемент появляется в
последующем, то есть единица появляется в двойке, двойка – в тройке и т.д.
И тогда самая первая идея состояла бы в том, что единица появляется
во всех n элементах, 2 в n-1, 3 – в n-2 и т.д. элементах. И тогда единицу
нужно было бы взять n раз, 2 – n-1 раз, тройку – n-2 раза и т.д. для
того, чтобы получить сумму всех чисел. Однако из рисунка 5 мы видим, что
единица появляется не во втором, а в третьем, а 2 появляется не в третьем, а
в четвертом. Другими словами, нечетные числа появляются в последующих
нечетных, четные числа появляются в последующих четных. Т.о. мы получаем как
бы два зеркала, смотрящихся друг в друга, но видящих не себя, а элементы
другого, причем, имеет место соответствие между этими элементами, то есть
каждому элементу одного можно поставить в соответствие единственный элемент
другого, и в этом смысле можно говорить о равномощности четной и нечетной
сторон чисел.
Отражение (свечение) чисел друг в друге.
Поставим вопрос так: сколько предшествующих точек светится
(появляется) в n2 ?
Число не
отождествленных точек n2 = Nn.
Относительно 1 мы можем сказать, что у неё нет предшествующих элементов. Но
если четные и нечетные числа суть противоположности, то это же самое мы
должны утверждать и относительно 2. Кажется, что для четных чисел
число 2 является таким же точно началом, как единица для нечетных чисел.
Начиная с трех мы можем говорить о том, что в его квадрате светится квадрат
единицы. Ведь квадрат 3 содержит в себе четыре квадрата двух, каждый по
четыре элемента.( И этим механизмом осуществляется
связь четных и нечетных чисел, последовательное явление противоположностей
друг в друге.)
Следовательно, получаем 16 точек. Квадрат 4 содержит 9 квадратов
3-х, и, следовательно, всего 36 точек. Квадрат 5 содержит 16 квадратов
и, следовательно, 64 точки. Итак, имеем: если нам дано n2,
то оно содержит (n-1)2 квадратов по четыре
точки в каждом. Поэтому (n-1)2 мы должны
умножить на 4. Но 4=22 Тогда получаем: Nn2=(n+2)2.
Например, N42=(4+2)2=36.
(Здесь обозначение Nn2
употребляется в качестве более точного синонима Nn=(n-1).
(Однако, если считать, что N есть сокращение для выражения "число не
отождествленных точек", то семантически такое отождествление несправедливо.
Однако мы не знаем в настоящем контексте отождествленных точек n, хотя в
натуральном ряде, можно подумать, мы имеем дело с отождествленными точками:
ведь число три содержит единицу и в нём появляется два, а число 2 есть
единица и в нём появляется единица. Т.о., в натуральном числе n светятся все
предшествующие ему числа, являясь в нём в виде своего рода призраков. Но
светиться - не значит отождествиться. Ведь мы не можем сказать ни об одном
предшествующем n числе натурального ряда, что оно является смежным с
каким-нибудь его членом. ) Или на пальцах: если n=4, то число плоскостей
квадрата n равно (n-1) в квадрате = 9, и, соответственно, число точек
плоскостей = 36.
Предшествующие числа отражаются (присутствуют в снятом виде) в
последующих. Это мы имеем уже в конструкции самого натурального ряда чисел:
двойка образована добавлением к единице единицы, тройка образована
добавлением к двойке единицы и т.д., и т.о. все предшествующие числа
оказываются включены в последующие, являясь материалом для их построения. В
квадратах то же самое, каждое предшествующее число отражается в последующем.
Мы видим, что в квадрате 3 в качестве центральной выступает точка, имеющая
максимальную глубину отождествления, равную 4, затем мы имеем глубину
отождествления, равную двум, у четырёх внешних внутренних точек (точки типа
2), представляющих, и, наконец, четыре внешние точки в собственном
смысле слова.
Если мы возьмём квадраты четного или нечетного ряда
чисел, то получим такую картины, что и действительно каждое последующее
число содержит неявным образом в себе все предыдущие. Если обратить внимание
на рис.5, но можно увидеть, что, например, квадрат 12 содержит в себе
квадраты всех предшествующих чисел: 10, 8, 6, 4, 2 Началом
натурального ряда чисел является не только единица, но и ноль.
Подойдем к объектам с точки зрения их становления. Здесь мы сталкиваемся с
двумя понятиями и взаимным переходом между ними: понятием точки и квадратной
плоскости, образованной четырьмя точками.
Пусть нам дан квадрат
единицы. Возникает вопрос, что он собой представляет? Что это может
означать: 1*1? Единица - это единица. Это, так или иначе, какая-то величина,
равная единице. Но если это величина, равная единице, то она имеет своё
начало и свой конец, и её конец обозначается единицей, а тогда её начало
может быть обозначено только нолём. Разумеется, мы можем говорить о том, что
единица - это просто какая-то отдельность. Но отдельности противостоит её
отсутствие. Отдельность принадлежит категории бытия. Отсутствию отдельности
противостоит категория небытия. Универсум характеризуется единством и
противопоставлением бытия и небытия. Поэтому если единица принадлежит бытию,
то ей с необходимостью противостоит ноль как представляющий небытие. Ноль
выполняет функцию, подобную той, которую выполняет мертвая вода в русских
сказках: он соединяет. Разрубили тело на десять кусков, полили мертвой водой
- и десять отдельных мертвых кусков соединились и образовали одно тело -
число 10. Полили число десять живой водой - и оно ожило, и им можно
пользоваться.
Но если так, то что такое эта отдельность в квадрате?
Например, мы имеем один огурец, и тогда возникает вопрос: что такое огурец в
квадрате? Для самой по себе неизменной отдельности этот вопрос бессмыслен.
Сколько единиц в таком квадрате? Это, конечно, не два огурца, потому что в
этом случае мы получили бы простое сложение двух объектов. Но вот если мы
рассматриваем единицу как неявным образом содержащую в себе ноль, и точно
также всякий объект как неявным образом содержащий, как своё отрицание,
ничто, то тогда мы, во всяком случае, можем хотя бы выделить единицу как
объект, потому что никакой объект не может быть выделен как таковой, если
отсутствует его отрицание как его противоположность.
В философском
плане мы имеем бытие и ничто, и мы можем выделить бытие лишь постольку,
поскольку ему противостоит ничто. Всё, что бы ни было, выделяется через свою
противоположность. И точно также объект выделяется через свою
противоположность - пространство, ведь пространство без объекта - это ничто.
Объект неявным образом содержит в себе пространство и определяет его собой,
как и, в свою очередь, пространство определяет себя через пространственные
свойства объекта. И т.о. нет объекта - нет и пространства, нет
пространства - нет и объекта.
А, между тем, в
натуральном ряде есть единица как представительница бытия, но отсутствует
ничто. А без ничто мы не можем определить и единицу. А ничто - это ноль.
Если так, то что такое единица в квадрате? Это квадрат, образованный в
(прямоугольной) системе координат четырьмя точками: 0,0 - начало координат,
0,1 - ось абсцисс, 0,1 - ось ординат, 1,1 - точка пересечения
перпендикуляров, восстановленных из единичных значений абсциссы и ординаты.
И, таким образом, мы получаем единичный квадрат, который явно себя не
проявляет.
Ноль принадлежит четной стороне натурального ряда, ибо
всюду, где число оканчивается им, мы имеем четное число, как и единица,
оканчивая число, делает его нечетным.
Квадрат числа проявляет себя в
последующих числах в виде квадратной плоскости ( квадрата).
Делаем
вывод: квадрат числа может существовать только как проявление
противоположностей бытия и небытия, чего-то и ничто, единицы и ноля.
Итак, мы образовали квадрат единицы. Квадрат двойки даёт нам явный
квадрат, содержащий четыре точки, и квадрат единицы проявился в квадрате
двойки, превратившись из объекта в себе в явный, чувственно данный объект, в
объект для себя. Мы получили своеобразное тождество квадрата единицы и
двойки в том смысле, что все точки квадрата двойки являются независимыми.
Возводим в квадрат тройку. В ней мы получаем 4 квадратных плоскости,
являющиеся явлением квадрата двойки в тройке, и при этом тройка образована
объектами трех видов, образованных разными степенями отождествления точек:
мы имеем одну точку, в которой совмещаются все 4 квадрата и представляющую
единицу; четыре совмещенные точки по две и четыре независимые ( не
совмещенные с другими ) точки, образующие собственно квадрат тройки. И т.о.
мы получаем число 9. Но, в то же самое время представительство четырех
квадратов оказывается беременно следующим квадратом, а именно, 4 квадрата
умноженные на 4 образующих их точки дают 16 точек, что соответствует четырём
в квадрате. Возводим 4 в квадрат, получаем 16. Число квадратов = (4-1)
в квадрате =9, и общее число точек квадратов =9*4=36 причем, четыре
точки представляют собой глубину отождествления, равную 4 и
представляют собой квадрат двух, 8 точек глубины отождествления, равную 2, и
четыре независимые точки. Но 36 - это 6 в квадрате, то есть квадрат
следующего четного числа.
Самопроизводство чисел
Вспомним, что исходная идея заключалась в том, что каждое число светится
во всех последующих числах. И, затем, что имеет место противоположность
четных и нечетных чисел. В связи с этим, займёмся опытами. Начнем с нечетных
чисел. Квадрат 1 есть единица. Квадрат тройки равен 9 точкам и четырем
квадратам, в которых одна точка имеет 4-ый уровень отождествления (то
есть является совмещением точек 4 квадратов), 4 точки имеют второй уровень
отождествления (принадлежат двум смежным квадратам), и 4 точки имеют первый
уровень отождествления, то есть принадлежат одному квадрату.
Квадрат 5 состоит из следующих совмещений: единица, над ней тройка
и затем идут четыре квадрата, представляющие квадраты трёх. Но эти четыре
квадрата есть не что иное, как свечение в квадрате трёх квадрата двух. И это
же самое свойство справедливо относительно четных чисел: в них также
светится квадрат предшествующего нечётного числа, как в квадрате
нечетного светится квадрат предшествующего четного числа. Однако
каждое из чисел светится в противоположном по четности предшествующем числе
в своей противоположной форме - квадрата, а не точки.
(Светиться - это значит являться, и свет оказывается явлением
сущности, таким, в котором явление, конечно, не совпадает с сущностью, ведь
в последнем случае невозможно было бы говорить о сущности, так как сущность
- это термин, который обладает смыслом только по отношению к своей
противоположности - явлению. Явление же характеризуется тем, что оно
представляет не себя, но что-то другое. Само же это различение явления и
сущности имеет в своём основании условный рефлекс, в котором условный
раздражитель представляет безусловный. Другими словами, различение
сущности и явления оказывается обусловлено существованием механизма
условного рефлекса)
Для чисел справедливо, что,
каждый следующий пояс квадратов чисел содержит в себе все пояса предыдущих
чисел. При этом следует различать число и его явление. Если форму квадратов
различать от формы точек, и точки рассматривать как представляющие
соответствующие числа явным образом, а квадраты - неявным, и если обратимся
к чувственным данным, то получим следующее.
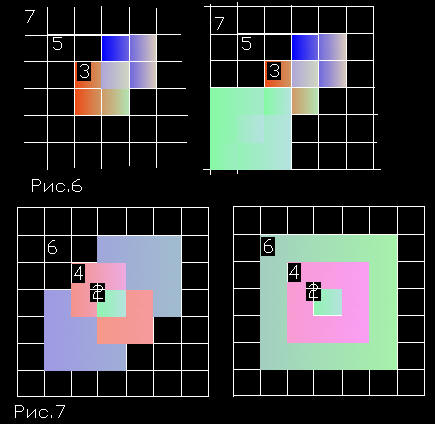
Возьмём число 3. На рис. 6
ему соответствуют 4 квадрата, что есть два в квадрате, и эти квадраты
содержат в себе 9 точек, что соответствует трём в квадрате. При этом
существует одна точка типа 4, соответствующая единице. Т.о. в 3-х
представлена единица в точечной форме и представлен квадрат двух в
квадратной форме.
Берем квадрат 5. Это 25 точек. Квадрат пяти образуется добавлением
очередного пояса квадратов, число которых равно 16, а это квадрат четырёх. У
квадрата пяти 9 точек типа 4, 12 точек типа 2 и 4 точки типа 1.
В пяти, как видим, снова в явной (точечной) форме присутствуют
предшествующие нечетные числа и в неявной форме (квадратов) присутствуют
четные числа.
Чем хороша математика - тем, что она позволяет ничему не верить. Она
имеет дело с созданными ею чувственными объектами, и не нужно ни о чем
догадываться, ничего отгадывать и, что самое важное, ничего придумывать от
себя. Нужно просто исследовать те закономерности, которым подчиняется
чувственно данный объект.
Поэтому не поверим, что подобного же рода закономерность справедлива
также и для четных чисел и обратимся для разрешения нашего сомнения к рис.
7. Для числа 2 в квадрате мы имеем один квадрат. Квадраты, как мы помним,
представляют число противоположной четности. Следовательно, один квадрат
соответствует квадрату единицы. И, соответственно, четыре точки типа 1, что
соответствует двум в квадрате.
Для квадрата числа 4 имеем один внутренний квадрат с точками типа 4 и
пояс из внешних 8 квадратов. Всего квадратов 9, что соответствует явлению
трёх в квадрате. И, наконец, число точек всех видов равно 16: 4точки типа 1,
4 точки типа 4 и 8 точек типа 2. Т.о., в квадрате четырех светятся квадраты
всех предшествующих точек.
Но то, чем мы занимаемся - это - доказательство путем
перебора возможных вариантов, число которых, однако, бесконечно. А
доказательство для бесконечности требует показать, что если некоторое
свойство имеет место для предыдущего числа, то оно будет иметь место и для
последующего.
n-3
Квадраты 7 содержат в себе квадраты пяти, трёх и единицы, . Т.о., квадрат
каждого последующего числа формируется посредством соответствующей добавки к
предыдущему, которая образуется внешним поясом квадратов. При этом
предыдущий квадрат оказывается представляющим только внутренние точки. И
поэтому число соответствующих квадратов должно быть умножено на четыре. Так,
квадрат 6 содержит в себе 9 внутренних квадратов с 16 отождествленными и 36
неотождествленными точками типа 4. Но 36 точек - это шесть в квадрате. Мы с
вами помним, что непосредственно квадрат 6 получается на основе
отождествления точек образующего его множества точек вида 1, 2, 4. Т.о.,
имеет место равенство между множеством неотождествленных точек квадрата 3-х
и множеством отождествленных точек квадрата 6: Non=Nn-3
Общее правило конструкции чисел включает в себя два принципа:
1. производство элементарных квадратов, состоящих из четырёх точек. 2.
Совмещение точек квадратов.
Вот формулы числа
внутренних к4n и внешних внутренних к2nквадратов,
где коэффициент при n указывает на число точек совмещения у квадрата и 4
внешних квадрата. Число внешних квадратов k1n
= 4 и внешний квадрат имеет две внешние внутренние точки и одну
внутреннюю и одну внешнюю точки (рис.8)
 kn
= k1n + k2n
+ k4n; k2n
+ k4n
= kn - k1n
= (n-1)2
-4 = (n+3)(n-1) (3) kn
= k1n + k2n
+ k4n; k2n
+ k4n
= kn - k1n
= (n-1)2
-4 = (n+3)(n-1) (3)
Из таблицы 1 получаем формулы для k2n
и k4n:
k2n = 4(n-3); k4n
= (n-3)2
И, т.о., мы получаем
набор формул для числа квадратов в зависимости от их вида.:
kn=(n-1)2
(1)
k1n = 4
(2)
k2n = 4(n-3) (3)
k4n
= (n-3)2 (4)
Nn=
4(n-1)2 (5)
Покажем, что
формулы (3), (4) верны для всех n>2. Для n=3 формула (3)выполняется. k2(n+1)
= 4(n+1-3)=4(n-2); (3a)
k2(n+1)=k2n+4=4(n-3)+4=4(n-2).
(3b) ; (3a)=(3b), ч.т.д.
Для k=3 формула (4) выполняется.
Приращение квадратов натуральных чисел un+1=2n+1,
тогда un-3+1= 2(n-3)+1=2n-5
kn+1
= (k+1-3)2=(k-2)2
(4a)
kn+1 = kn
+ un+1 = (n-3)2
+ 2n -5 = n2-4n + 4 = (n-2)2
(4b). (4a)=(4b), ч.т.д.
Число неотождествленных
точек квадратов мы обозначили через Nn;
соответственно, число внешних, внешних внутренних и внутренних точек
обозначим через N1n, N2n,
N4n. Nn=
N1n +N2n
+N4n =(n+22
(11) Соответственно, число отождествленных точек
будем обозначать буквой "о" перед n: Non= N1оn
+N2оn
+N4оn = n2
(12)
| Таблица 1 числа квадратов n, внешних, внешних
внутренних и внутренних квадратов
|
| n |
n2 |
kn=(n-1)2 |
k1n =4 |
k2n=4(n-3) |
k4n = (n-3)2 |
| 1 |
1 |
0 |
4 |
|
|
| 3 |
9 |
4 |
4 |
- |
- |
| 4 |
16 |
9 |
4 |
4 |
1 |
| 5 |
25 |
16 |
4 |
8 |
4 |
| 6 |
36 |
25 |
4 |
12 |
9 |
| 7 |
49 |
36 |
4 |
16 |
16 |
| 8 |
64 |
49 |
4 |
20 |
25 |
| 9 |
81 |
64 |
4 |
24 |
36 |
| 10 |
100 |
81 |
4 |
28 |
49 |
Всякий последующий квадрат числа являет себя из превращенной формы предыдущих, и
это явление состоит в том, что точка предыдущего числа превращается в квадратную
плоскость с ограничивающими её четырьмя точками в последующем, чем квадрат как
представляющий одну точку "снизу", увеличивает число точек в 4 раза "сверху". И
затем путем совмещения множества точек и их отождествления получается
число.
Пусть n=1, тогда n2 =1.
Число соответствующих квадратов кn=(n-1)2
= 0.
n=2, тогда n2
=4. Число соответствующих квадратов кn=(n-1)2
= 1. Один квадрат содержит в себе 4 точки, которые соответствуют значению n2
n=3, тогда n2 =9. Число
соответствующих квадратов кn=(n-1)2
= (3-1)2 = 4. Из них число внутренних
квадратов к4n= (3-3)2=
0.Соответственно, число внешних внутренних квадратов равно 0. Остаются 4 внешних
квадрата. Внешние квадраты характеризуются тем, что имеют по две внешние
внутренние точки и одну внутреннюю точку и одну внешнюю. Т.о. всего
внешние квадраты имеют имеют N1n=4k1n=16.
Далее нам понадобятся правила определения числа видов точек в зависимости от
числа квадратов. Пусть нам дано произвольное n, и мы из него образовали квадрат.
Как мы можем представить квадрат чувственно? Квадрату числа соответствует
квадрат объектов, в настоящем случае точек или плоскостей, таких, что число
элементов, образующих их столбцы и строки, одинаково. Представим себе квадрат из
n точек. Будем считать, что к внешним точкам или плоскостям относится "внешний
пояс" точек или плоскостей. Для того, чтобы получить квадрат без внешнего
пояса объектов, нужно убрать из него объекты внешнего пояса, а это не что иное,
как произведение (n-1) строки на (n-1) столбца, то есть (n-1)2
Для нас в данном случае важно связать чувственный образ с его математическим
выражением и математическими действиями над нам. Нарисуйте на бумаге или
представьте в уме прямоугольник, образованный 4 квадратами в высоту и шестью
квадратами в ширину. Число квадратов равно 4*6=24. Запишем 4*5=20. Мы отсекли с
правой или левой стороны прямоугольника 4 квадрата. 3*6=18 - тем самым мы
отсекли сверху или снизу квадрата 6 элементов. Т.о., применяя к исходному
объекту разные математические операции, мы получаем новые объекты. Вот эту связь
между числовым представлением объекта и его чувственным образом важно
последовательно проводить, так как чувственный образ показывает нам наглядно,
что именно и почему мы делаем в чувственной сфере, применяя к ней те или иные
математические операции. Математические операции являются средством
изменения, преобразования чувственной сферы сначала идеально, а затем эта
идеальная сфера может быть перенесена на действия с реальными объектами.
В тексте используются два вида объектов - точки и квадраты и
переходы от одних к другим. В формулах (1)-(5)даны переходы от точек,
соответствующих квадратам чисел, к квадратам. Поэтому следовало бы различать, с
какого рода объектами мы имеем дело - с точками или квадратами. Для этой цели
число точек будем обозначать буквой n, число квадратов - буквой к, и нам
нужно связать величины n и k. Числу k соответствует n-1. Действительно, нетрудно
видеть, что число точек образует множество строк и столбцов, такое, что между
любыми двумя строками или столбцами точек укладывается n-1 полоса квадратов.
Итак, k=n-1 (6).
Если дано число квадратов,
то они в нашем воображении должны быть организованы в соответствующую квадратную
форму, а не в какую бы то ни было иную, например, линейную. В квадратной
форме у нас оказывается неявно представлено уравнение, выражающее число
квадратов кn,
так как строки и столбцы соответствуют n, а форма квадратов
образует квадрат n.
До сих пор использовались понятия внешних и внешних внутренних
квадратов и соответствующих им точкам. Говорилось, что все внешние (включая в
это понятие и внешние внутренние) квадраты характеризуются двумя точками вида 2,
при этом внешние внутренние квадраты характеризуются двумя точками типа 4, а
внешние в собственном смысле квадраты характеризуются одной точкой типа 1 и
одной точкой типа 4. Но все точки типа 4 учитываются при расчете внутренних
квадратов, в которых каждая из точек совмещается либо с двумя внешними
внутренними точками и одной точкой смежного внутреннего квадрата или с одним
внешним квадратом. Либо, наконец, совмещается с тремя внутренними
квадратами. Это хорошо видно на рис.9.
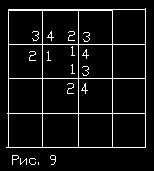
Поэтому можно брать все внешние
квадраты kв. Нетрудно видеть, что kвn=к1n+k2n
[(8)]=4(n-1) , Итак, kвn=4(n-1)
(7) , И, наконец, остаются четыре неучтенные внешние точки внешних в собственном
смысле квадратов.
Итак, определено число видов квадратов к1n,
к2n
к4n, если известно общее
число квадратов кn: kn=
k1n +k2n
+k4n = k2n
+k4n (8)
Теперь следует определить формулы числа точек, соответствующих наборам
квадратов.
Но вначале обсудим вопрос отождествления, на котором
покоится формирование чисел. Выражение "точка типа2" говорит о том, что
отождествляются между собой две точки. Это значит, что две точки
приравниваются к одной, или, напротив, одна точка представляет, неявно
содержит в себе две точки. Мы берем все квадраты сами по себе. То есть
смежные квадраты рассматриваются как самостоятельные квадраты.
Отождествление точек, принадлежащих разным квадратам, непосредственно
связано со смежностью квадратов. В зависимости от того, какое число точек
совмещается, в зависимости от этого стоит уровень отождествления точек, и в
случае с квадратами мы имеем два возможных варианта отождествления:
отождествляются либо две точки, либо 4. Т.о., набор правил заключается в
том, что, с одной стороны, мы вычисляем общее число точек. Так, для n=4
n2=16, соответствующее n число квадратов k4
= 9,. Число точек типа 2 для n равно N2n=2(4(k2n-1)
= 8 Отсюда получаем n2=Nn=N1n+N2n+N4n=4+8+4=16
При рассмотрении числа точек должно быть явно указано, какие точки
квадратов имеются ввиду: отождествленные или не отождествленные.
Число не отождествленных точек квадратов любых типов равно 4кn.
Однако когда речь идет о типах квадратов, то здесь внешние квадраты свои
точки типа 4 как бы передают точкам внутренних квадратов, с которыми они
являются смежными; аналогично, внешние внутренние точки внешние квадраты
передают внешним внутренним квадратам, а свою внутреннюю точку - внутренним
квадратам. И т.о. специфические точки одних квадратов учитываются в других
квадратах, и расчет точек квадратов осуществляется, исходя из этого правила.
Т.о. получаем правила для выражения числа отождествленных и не
отождествленных точек в связи с числом квадратов.
NК=4К
(11), NсК=(k+1)2
(12), где k = √K (10) Следует помнить, что буквой N всегда
обозначается число точек. Поэтому выражение NК
читается как "число точек К квадратов. Выражение NcK
- как число отождествленных точек смежных квадратов, и т.д.
Нужно иметь
различение между числом квадратов, которое является квадратом некоторого
числа, и
этим числом. Это число выше определено как k. Соответственно,
число квадратов обозначим через K
N1K=N1сK=4;
N2K=8(k-2); N2сK=4(k-2);
N4K=4К; N4сK=(k+1)2.
точек внутренних квадратов N4k
= 4кnхарактеризуетcя тем, что, с одной
стороны, каждая точка внутреннего квадрата отождествлена с тремя точками
других квадратов. С другой стороны, каждый из квадратов содержит по четыре
точки. Поэтому число точек квадратов типа 4 равно
N4k
= 4kn
(9)
Из формул (3), (6) имеем: k2n=4(n-3)=4(k-2)
(10), соответственно, число точек внешних внутренних квадратов
равно N2k=2(4(k-2))=8(k-2) (11),
N1k=4 (12).
Закономерности мышления
Когда строится какой-то объект, то его строительство осуществляется на
основе данных бессознательного. На основе данных, которые нужно
рационализировать, то есть перевести на язык сознания, язык слов. Ведь когда
мы имеем дело с интуицией, то мы говорим, что нечто чувствуем. И тогда
возникает вопрос о словесном выражении чувствования. Работа сознания по
нахождению словесного выражения интуиции в качестве своего результата даёт
систему понятий. Однако процесс построения понятий сопровождается
постепенной дифференциацией данных интуиции, и поэтому этот процесс
представляет собой постепенный процесс уточнений, изменения исходных
понятий, что в этом процессе постоянных изменений и уточнений, конечно,
затрудняет понимание..
Однако любая интуиция в конечном счете
переводится на уровень сознания в той мере, в какой это обусловлено пользой.
И текст доводится до такого уровня, когда им уже можно пользоваться.
Настоящий текст в известной мере можно рассматривать в качестве базового.
Если это окажется действительно так, то мы будем к нему возвращаться и
прояснять. Ну, а если нет, то на нет и суда нет. Польза текста может быть
обусловлена тем, интуиция порождается предыдущими процессами, которые
вызвали её к жизни в связи с нерешенностью каких-то проблем. На настоящем
этапе носитель интуиции полагает, что уровень её осознания у него
достаточен для того, чтобы можно было ею пользоваться. И поэтому он
возвращается к проблеме, которая породила интуицию.
Необязательное дополнение
Обратимся к закономерностям, связывающим внешние внутренние точки. Для n=3
мы имеем четыре квадрата с четырьмя отождествленными внутренними точками и,
соответственно, с 8 неотождествленными. Отождествленные точки равны квадрату
двух, неотождествленные - третьей степени двух.
Теперь возьмём
высказанное положение и на его основе построим табличную форму для
разных значений n. . Согласно высказыванию, последовательность столбцов
соответствующей табличной формы такая: n, n2,
кn - число квадратов квадрата n, No2n
- число отождествленных точек типа 2n, N2nчисло
не отождествленных точек типа 2, 2o2nm-
степени двух квадратов отождествленных точек типа 2n, 22nm-
степени квадратов двух неотождествленных точек типа
2n. Получилось 7 столбцов, и возьмём 12 строк.
| n |
n2 |
кn=(n-1)2 |
No2n=4(n-2) |
N2n=8(n-2) |
2o2nm |
22nm |
| 0 |
0 |
- |
- |
- |
- |
- |
| 1 |
1 |
- |
- |
- |
- |
- |
| 2 |
4 |
1 |
- |
- |
- |
- |
| 3 |
9 |
4 |
4 |
8 |
22 |
23 |
| 4 |
16 |
9 |
8 |
16 |
23 |
24 |
| 5 |
25 |
16 |
12 |
24 |
23+22 |
24+23 |
| 6 |
36 |
25 |
16 |
32 |
24 |
25 |
| 7 |
49 |
36 |
20 |
40 |
24+22 |
25+23 |
| 8 |
64 |
49 |
24 |
48 |
24+23 |
25+24 |
| 9 |
81 |
64 |
28 |
56 |
24+23+22 |
25+24+23 |
| 10 |
100 |
81 |
32 |
64 |
25 |
26 |
| 100 |
1000 |
9801 |
392 |
784 |
27+26+23 |
28+27+24 |
Таблица проявляет следующую
закономерность: - Для всех слагаемых степень квадрата 2 не
отождествленных чисел на единицу больше степени квадратов 2 отождествленных.
- В сумме слагаемых каждая следующая слева направо степень двух
меньше предыдущей.
- Степени первого (слева направо) квадрата 2
Внутренние точки
| n |
n2 |
кn=(n-1)2 |
No4n=(n-2)2 |
N4n=4(n-2)2 |
2o2nm |
22nm |
| 0 |
0 |
- |
- |
- |
- |
- |
| 1 |
1 |
- |
- |
- |
- |
- |
| 2 |
4 |
1 |
- |
- |
- |
- |
| 3 |
9 |
4 |
1 |
4 |
20 |
22 |
| 4 |
16 |
9 |
4 |
16 |
22 |
24 |
| 5 |
25 |
16 |
9 |
36 |
23+20 |
25+22 |
| 6 |
36 |
25 |
16 |
64 |
24 |
26 |
| 7 |
49 |
36 |
25 |
100 |
24+23+20 |
26+25+22 |
| 8 |
64 |
49 |
36 |
144 |
25+22 |
27+24 |
| 9 |
81 |
64 |
49 |
196 |
25+24+20 |
27+26+22 |
| 10 |
100 |
81 |
64 |
256 |
26 |
28 |
Получены выражения, соответствующие двоичной системе исчисления
|






 как
процесс. Каким образом может быть представлено всё дело. Пусть у нас
существуют квадраты натуральных чисел. Тогда, взяв соответствующее число
квадратов, получим куб. Но эти квадраты, присутствующие в кубе, могут
рассматриваться как соответствующее число карт соответствующего рода. Мы
можем также образовать из полученных наборов карт кубические объекты,
соединив соответствующие точки. При этом количество точек не изменится.
как
процесс. Каким образом может быть представлено всё дело. Пусть у нас
существуют квадраты натуральных чисел. Тогда, взяв соответствующее число
квадратов, получим куб. Но эти квадраты, присутствующие в кубе, могут
рассматриваться как соответствующее число карт соответствующего рода. Мы
можем также образовать из полученных наборов карт кубические объекты,
соединив соответствующие точки. При этом количество точек не изменится.  kn
= k1n + k2n
+ k4n; k2n
+ k4n
= kn - k1n
= (n-1)2
-4 = (n+3)(n-1) (3)
kn
= k1n + k2n
+ k4n; k2n
+ k4n
= kn - k1n
= (n-1)2
-4 = (n+3)(n-1) (3)