a1 Обозначения
Обозначения: & - конъюнкция (
союз "и"), V - дизъюнкция (союз "или"), X,Y,Z - переменные высказываний,
принимающих
значения "истина", "ложь", S, A, B - метазнаки, обозначающие высказывания,
простые или сложные (под последними понимаются высказывания, содержание
операторы логики высказываний "и", "или", "если...то..." и т.п.) ,
Ⱶ -знак вывода
Пусть дана тождественно-истинная формула S=A→В,
смысл которой сводится к тому, что если
S истинно, то если допустить, что
истинно А, то будет истинно и В.
а2
Тавтологии
Что такое тождественно-истинная формула?
Согласно определению, тождественно-истинная формула - это формула, истинная
при всех возможных наборах значений входящих в неё переменных. На деле же
речь идёт о тавтологии. Но тавтологии не допускаются в логике: нельзя
доказать нечто через нечто. И, однако, вся логика строится на тавтологиях.
Законы логики - это тавтологии. Чем различаются члены тавтологии? -
различной формой, которая говорит об одном и том же.
Можно говорить о содержании и о форме и об отношении между ними. С одной
стороны, разные содержания могут выражаться одной и той же формой. Когда
говорят о многозначности языка, имеют ввиду именно это. С другой стороны,
разные формы могут выражать одно и то же содержание.
Вообще тавтология в логике связана с разными способами упорядочивания
объектов. С разными порядками, которые обладают одинаковым содержанием и
поэтому могут быть использованы один вместо другого.
Но это - полярности. А между полюсами находятся переходные отношения
этих двух сторон, формы и содержания, находятся переходные процессы от
одного полюса к другому. Поэтому одна сторона так или иначе дополняется
другой. Тождественная форма дополняется разным содержанием, а содержание
выражается в несоответствующей ему форме. Тем не менее, общая тенденция,
общее стремление состоит в достижении соответствия противоположных сторон,
содержания и формы.
еще мысли.
тавтология -это формула, истинная
для всех наборов истинностных значений. Тождественно - ложная формула - это
формула, ложная для всех возможных наборов истинностных значений. Каково
отношение между этими двумя противоположными формулами? Ведь если существуют
аксиомы и пр. для тождественно-истинных выражений, то подобного же рода, но
противоположные, должны существовать также и формулы для тождественно-ложных
формул. В связи с этим, возникает также вопрос о двух противоположных
логиках с их противоположными правилами. И это будет истинное противоречие.
Во всяком случае мы получаем две противоположные логики, и в связи с этим
возникает вопрос об отношении между ними. Так как обе логики симметричны, то
есть обладают всеми соответствующими операторами, то в отношении правил
вывода, а также систем аксиом и формул они полностью идентичны. И, в то же
самое время, то, что является оператором в одной логике, является отрицанием
его в другой логике. Т.о., мы получаем две вещи. 1. две тождественные, но
противоположные логики. противоположность их заключается в том, что то, что
является истинным в одной логике, ложно в другой, и обратно. Т.о., мы
получаем 4 вещи: две логики с их внутрилогическими высказываниями. И две
вещи, связанные с оценкой высказываний одной логики в другой. Собственно,
здесь также имеет место симметрия, которая заключается в отрицании всех
высказываний противоположной логики. Но это же самое должно относиться также
и ко всем тождественным формулам логик. Это должно позволить
осуществить переход от формул одной логики к формулам другой логики. При
этом рассмотрение операторов должно начинаться с противоположных крайних
строк истинностной таблицы, то есть для логики истины начинаем с первой
строки и идём к последней для логики лжи начинаем с последней строки и идем
к первой. Благодаря этому мы сохраняем симметричный (равный) подход к
противоположным логикам. Правила же всех операторов определяются одинаково
для обоих операторов. Понятия истины и лжи являются относительными
понятиями. Приняв одну сторону противоположности за истину, мы тем
самым определяем другую сторону противоположности в качестве лжи, как
и обратно.
Какого рода отношение между операторами в противоположных
логиках мы получаем? Пусть дана импликация для логики истины (логики И).
Тогда ,если мы возьмём дополнение к оператору отрицания, то получим обратную
импликацию логики лжи (Логики Л). Пусть нам дано высказывание: вода при
нагревании расширяется (если А: воду нагревать, то она В будет расширяться).
Для определения оператора, противоположного импликации, мы должны сначала
перейти к оператору логики И, представляющему отрицание оператора
импликации. Получим конъюнкцию в логике И А&-B.
Берем дополнение к этому оператору, начав рассматривать в качестве основания
(точки отсчета), объект под названием "л", который понимается как истина и
будем рассматривать соотношение истинностных значений снизу вверх в таблице
операторов. В результате получим обратную импликация. Действительно, л,л
дают л; л,и дают л; и,л дают и; и,и дают л. Обратимся к импликации И,
чтобы выяснить, чем отличается прямая импликация от обратной. Получим: если
А, то В и А, если В. Тогда в обратной импликации получим
1. Таблица бинарных операторов.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Чтение обозначений: ти, тл -
тождественно-истинная,
тождественно-ложная формула. v - дизъюнкция,
оби - обратная импликация, и - импликация, ~ -эквивалентность,&- конъюнкция,
о& - отрицание конъюнкции, сv - строгая дизъюнкция, ои - отрицание
импликации, ооби - отрицание обратной импликации, оv - отрицание дизъюнкции.
Мы фактические получили две противоположные логики: положительную и
отрицательную. В таблице бинарных операторов употребляются два знака: 1,0. В
положительной логике знак 1 читается как "истина", знак 0 - как "ложь".
Слово "истина" будем обозначать знаком "и", слово "ложь" - знаком "л".
В логике отрицательной знак 0 читается как истина, знак 1 - как ложь.
И еще у нас был алгоритм (технология) перехода от одной логики к другой:
берется оператор одной логики, берется его отрицание, и в полученной таблице
изменяются значений 1,0 на противоположные, после чего определяется
соответствующий оператор противоположной логики. Очевидно, что высказывания
двух логик должны соответствовать друг другу и быть оба истинными.
Будем переходить от логики истины (положительной логики) к логике лжи
(отрицательной)
Мы будем выбирать какой-то из
операторов. Там дана таблица операторов положительной логики. В ней
оператору импликации соответствует таблица 5. Теперь рассмотрим заданную
таблицу с точки зрения значений отрицательной логики. В принципе,
безразлично, какой порядок строк для наборов истинностных значений
переменных А, В мы изберем. Но примем привычный порядок, а для этого нужно
начинать с последней строки и идти от неё к первой. Примем форму (порядок):
[№ строки (х,у=Х,У)=(z=Z)].
Получим:[ 4 (0,0 = и,и
) = (0 = и
)]; [ 3 (0,1
= и, л ) = (1
= л
)]; [ 2 ( 1,0
= л,и ) = (0
=
и )]; [ 1
(1,1 = л,л
) = ( 0
= и )] Получаем в строках 1234
значения 0010, и ищем в таблице номер оператора, которому этот набор
значений соответствует. Это оператор 14 - оператор обратной импликации.
Посмотрим, как это будет выглядеть на содержательном уровне. Возьмём
высказывание: Если А обладает свойством а, то В обладает свойством в:
А(а)→В(в).
Обратим внимание на эту форму: А, В рассматриваются как
какие-то объекты определенного рода, то есть это не человек вообще, не
понятие человека, не общее, а - человек. Разумеется, отдельный объект
способен обладать множеством свойств, которые к тому же находятся в каких-то
отношениях между собой. А отсюда мы переходим к логике,
противоположной принятой логике множеств , в которой рассматриваются
отношения между свойствами объектов, а не между объектами.
В противоположной логике, соответственно, А не обладает свойством
а: А(-а), В не обладает свойством с:В(-в). Так как выражение обратной
импликации читается как А, если В, то получаем: А не обладает
свойством а, если В не обладает свойством в: А(-а)←В(-в).
Выражения А(а) и подобные им являются высказываниями, так как в них
определены и субъект и предикат. А(а) - утвердительное суждение, А(-а) -
отрицательное. Сокращая, мы можем обозначить высказывания одной буквой.
Например, А(а)=р, соответственно, А(-а)=-р. В(в)=q,
В(-в)=-q, отсюда получаем
тождественно-истинную формулу р→q
~ р←q
Но у нас а, в -некоторые определенные свойства. Но вместо определенных
свойств могут быть подставлены какие угодно другие. И тогда выражение А(х),
где х - переменная свойства, представляет собой функцию, зависящую от
значения х. В чем вообще состоит познавательный человеческий процесс? В том,
что рассматриваются объекты какого - то рода. При этом действуют всегда с
единичными объектами. Познание заключается в том, чтобы установить, что
объекты обладают какими-то свойствами в некоторых заданных условиях, которые
определяются какими-то другими объектами, свойства которых контролируются. А
что такое свойства, которые определяются? это какие-то неизвестные, значение
которых нужно определить. Мы можем определить область из множества
свойств, и пытаться определить, существует ли в этой области подходящее
свойство.
79.
Операторы противоположных логик.
80. Чтение вкусовыми сосочками языка.
81. Познание состоит из двух этапов: постепенных
количественных изменений и качественного скачка. Постепенные количественные
изменения занимаются непосредственно материалом, с которым имеют дело.
Качественный скачок открывает новую область чувственного познания, которую
нужно исследовать со стороны объективных закономерностей, которые действуют
в ней. И затем происходит очередной качественный скачок, открывающий
качественно новые области для исследования.
82. Если у нас есть некоторое свойство а объекта А, то
характеристики этого свойства определяются внешними критериями. То есть это
свойство в объекте А как системе должно удовлетворять каким-то параметрам
для того, чтобы А могло обладать некоторой функцией. А эти требования
определяются, очевидно, внешними задачами, которые должно решать А.
83. В логике истины конъюнкция в логике лжи соответствует
дизъюнкция. В логике истины дизъюнкции в логике лжи соответствует
конъюнкция.
84. Отрицание оператора – это изменение его истинностных
значений на противоположные.
85. Отрицанию импликации в логике истины соответствует
обратная импликация в логике лжи. И отрицанию обратной импликации в логике
истины соответствует импликация в логике лжи.
Нам дана таблица 1. Линия между
строками 2 и 3 может рассматриваться как линия симметрии противоположных
логик . В зависимости от того, как мы интерпретируем значения 1,0, мы
получаем логику истины или логику лжи. Логику истины будем рассматривать в
порядке строк 1,2, 3,4, логику лжи - в порядке строк 4,3,2,1. В результате
будут получены одинаковые соотношения истинностных значений, так как,
например, набору 1,1 в логике истины соответствует набор 0,0 в логике лжи.
Теперь рассмотрим технологию, которой определяется
соответствие, то есть эквивалентность операторов в разных логиках.
Возьмём набор истинностных значений для импликации в ли
(логике истины. Лл-логика лжи). Это -5-й оператор с истинностными значениями
илии. В логике лжи этот же самый набор имеет вид лилл, что соответствует
обратной импликации. Если мы захотим перевести оператор обратной импликации
лл на язык ли, то получим 12 оператор.
Т.о. мы получаем понятия положенного и снятого. Оператор
5 ли есть вещь положенная. В то же самое время в снятом виде в нем
содержится оператор обратной импликации, который в положенном виде выступает
в ли 12 оператором. Снятый оператор 5лл и положенный оператор 12ли - это в
содержательном отношении два тождественных оператора. Две логики отличаются
друг от друга тем, то оперируют противоположными истинностными значениями.
Рассмотрим свойства прямой и обратной импликации. Прямая
импликация говорит: Если А, то В. Интерпретировать это высказывание можно
различно. Можно рассматривать это высказывание как выражающее временное
отношения предшествования события А событию В. Можно это высказывание
интерпретировать как отношение включенности множества А в множество В.
Обратная импликация гласит: -А, если -В.
Действительно, с теоретико-множественной точки зрения
если А, то В, то если -В, то -А. То же самое, если мы возьмём простую
временную последовательность событий, то если -В, то, конечно, -А. Обратная
импликация может быть заменена на тождественную ей прямую: А, если В тогда и
только тогда, если В, то А. По сути, это - две формы выражения одного и того
же отношения.
Когда мы имеем дело с высказываниями, то всегда должна
быть определена область, по отношению к которой высказывания делаются, так
как в противном случае высказывания теряют свой объективный критерий истины,
и их верификация становится невозможной. Вы, конечно, можете объявить любое
высказывание истинными или ложным, но это совершенно не означает, что с вами
обязаны будут согласиться другие люди. Вы можете сказать, что некоторое
высказывание истинно, а другое высказывание ложно, потому что это вам
нравится. Но тогда в качестве критерия высказывания будет выступать то, что
вам нравится, и точно таким же критерием это должно стать для окружающих,
если вы хотите, чтобы истинностное значение суждения начало носить общий
характер. Разумеется, сие часто случается, когда в обоснование истинности
суждения приводится субъективный аргумент. И всё это может действовать, если
массы заражены подобного рода субъективностью. Но в этом случае
субъективность превращается в объективный закон, то есть объективность
субъективируется.
А*
В*
Аи→Ви
Ал→Вл
и
и
и
л
и
л
л
л
л
и
и
и
л
л
и
л
А*
В*
Аи→Ви
Ал→Вл
Аи˅Ви
Ал˅Вл
Аи&Ви
Ал&Вл
Аи≡Ви
Ал≡Вл
Аи↓Ви
Ал↓Вл
Аи→Ви
Ал→Вл
Аи→Ви
Ал→Вл
и
и
и
л
и
и
и
и
и
л
л
и
и
л
л
л
и
л
л
и
л
и
и
л
л
и
и
и
и
л
л
и
л
и
и
л
л
л
и
л
л
л
л
л
и
л
л
и
Какой принцип рассмотрения: для нас важно, как будет выглядеть это же
самое высказывание в противоположной логике.
В обоих логиках мы имеем дело с одним и тем же оператором.
Но при этом в глазах противоположной логики это будет уже другой оператор.
Например, оператор дизъюнкции в одной логике выглядит как конъюнкция в
другой. Например, пусть в логике истины высказаны в качестве истинных
высказывания Все стало вокруг голубым (А) и зеленым (В). В противоположной
логике мы получим -А, -В, и, значит, всё стало вокруг и не голубым, и не
зеленым, однако в противоположной логике это будет выглядеть как "Всё
стало вокруг" голубым или зеленым .
Всё определяется
тем, как мы относимся к объекту- как к положительному или отрицательному, а
этим определяется и то, рассматриваем мы нечто как истинное или ложное.
В связи с этим, мы должны различать субъективно и объективно истинное.
Мы рассматриваем логику с психофизиологической, а именно, инстинктивно-рефлекторной стороны, потому что деятельность именно этой сферы представляет собой д=практическую действительность человека. Что такое рефлекс? Это механизм, обеспечивающий адекватные отношения субъекта с внешней средой. Человек рождается как инстинктивное существо, и в этом, как и всякого живого существа, выражается его активность по отношению к внешней среде. Другими словами, в инстинкте человека являются в настоящем навыки действий его предков. Этим навыкам противостоит реальность, к которой человек должен приспособиться. Т.о., с одной стороны человек имеет реальность, с другой - отражение им этой реальности, и рефлекторным механизмом обеспечивается их соответствие.
Поэтому когда мы говорим о тавтологии как повторении одного и того же, необходимо иметь ввиду, что всякое тождество дополняется противоречием, а тавтология - противоположным содержанием. Для того, чтобы логика была не абстрактной, чисто теоретической наукой, но наукой жизни, она не должна вся сосредоточиваться на форме, но иметь ввиду содержание. И если тавтология в качестве формы выражения - это тождество, то с необходимостью это тождество должно заключать в себе противоположность, а эта противоположность есть отношение между тем, что есть, и его отражением. Особенность человеческого отношения с внешней средой состоит в том, что своё знание о внешней среде он отождествляет непосредственно с внешней средой, тогда как в реальности это - не одно и то же, и эти две стороны могут как соответствовать, так и противоречить друг другу. Это отношение между бытием и знанием, отражением реальности и реальностью и выражается в основном законе логики - законе тождества: если р, то р. Необходимо заметить, что закон тождества имеет три формы. Условно примем, что левая часть уравнения представляет реальность, а правая - её отражение. Это обстоятельство можно выразить обозначениями л, п: рл, рп. Общее требование, как известно, это требование тождества, а, точнее, соответствия. Тогда, если мы говорим если рл, то рп, то мы имеем ввиду, что отражение рп должно приводиться в соответствие с реальностью рл, то есть должно иметь место формирование адекватного реальности отражения. Если же мы говорим если рп, то рл, то мы утверждаем уже противоположный тезис, требующий соответствия реальности отражению, то есть тем инстинктам, которыми определяется самореализация субъекта. Теперь допустим, что доминирует процесс приспособления субъекта к реальности. Тогда получаем цикл системы с обратной связью: есть реальность, она отражается. Субъект, действующий на основе полученного отражения, достигает равновесия с внешней средой, то есть работает формула: (pл→рп)→(рп→рл). В целом вывод запишется так: рл, рл→рп Ⱶ рп; рп, рп→рлⱵ рл. Убираем промежуточные члены и получаем рл→рл. Либо же обратное отношение (оставляем в качестве упражения). Получим рп→рп. Как видим, мы получили две противоположные формы тождества рл→рл и рп→рп, такие, что за ними стоит их противоположность. Эти два отношения к реальности, в котором доминируют реальность либо субъект, могут быть объединены в единство рл↔рп. В этом выражении в снятом виде содержится две противоположные формы доминирования реальности или субъективности.
Если мы имеем дело с реальными чувственно-практическими отношениями субъекта с внешней средой, то в этих отношениях мы можем выделить точки времени, в которых достигается отношение тождества реальности и её отражения в бытии человека, и множество переходных процессов, в которых формируется либо отражение, начиная с некоторого ноля и закачиваясь единицей, либо же формирование реальности на основе существующего у субъекта образа, то есть идеального, и процесс заключается в отражении идеального в реальность. Точки тождества можно назвать узловыми точками процесса. Точки тождества - это точки достижения истины. Но всякое тождество р→р начинается с единичного значения, скажем, рл, реальности, и заканчивается рп, или идеальным. Вначале процесса идеальное, условно говоря, равно нолю, Весь переходный процесс заключается в формировании отражения реального в идеальное. И когда содержание идеального начинает отражать содержание реальности, тогда говорят, что истина достигнута, и имеет место р→р. Но это - всего лишь момент процесса. Если же мы теперь удалим из рассмотрения переходные процессы, то мы окажемся среди множества постоянных, "вечных" истин, порожденных ими. С другой стороны, из сказанного видно, что выражение р→р есть, с одной стороны выражение для осуществляющегося процесса, а, с другой стороны, в результате становления мы имеем дело с результатами - соответствием отражения и отражаемого. Поэтому нужно различать, с чем мы имеем дело, с процессом или результатом.
Применяемый метод: берется рассуждение как полученное в результате некоторого инстинктивно-рефлекторного процесса, и затем рассуждение исследуется с точки зрения применяемых в нём оснований.. Т.о., мы не строим некоторое "правильное" рассуждение, а берем рассуждение так, как оно есть, и предполагаем, что оно правильно, а затем исследуем, в чем именно заключается его правильность, на чем она основывается, на каких положениях. Рассуждение можно рассматривать в качестве правильного, если оно работает, и в качестве неправильного (хотя бы оно и было логически верно), если оно не работает. Иначе: Существует цель, которая реализуется в какой-то ситуации. Цель реализуется посредством рассуждения. Если действия на основе рассуждения приводят к реализации цели, то оно (рассуждение) верно. В противном случае оно неправильно.
Пусть дана формула S = А→В= (XV(Y&Z))→((XVY)&(XVZ))
Как мы рассуждаем: А истинно, если истинно по крайней мере одно из двух: Х или Y&Z.
Допустим, истинно Х, тогда истинно ХVY, XVZ и, следовательно, истинно В = ((XVY)&(XVZ))
Допустим, что истинно Y&Z. Тогда истинны Y и Z, и, следовательно, истинны XVY, XVZ, откуда истинно В = ((XVY)&(XVZ). Обратите внимание на то, что весь вывод вы делаете автоматически, и если вы зададите себе вопрос, почему вы построили вывод именно таким образом, вы на этот вопрос не ответите. Вы сделали все правильно, и, однако, вы не можете сказать, почему всё то, что вы сделали, правильно. То есть вы не можете утверждать, что ваши действия истинны. И именно в силу автоматичности ваших действий, автоматичности, которая основывается на чувстве, что действовать нужно именно так, а не иначе. Вопрос же, почему вы именно так действовали, остается у вас за скобками. Другими словами, вы действовали в соответствии с существующим в вас стереотипом, то есть в соответствии с рефлексом, который приобрел признаки инстинкта, который для вас не требует доказательства именно потому, что он всегда приводит к одним и тем же результатам при некоторых постоянных условиях.
Вы можете задаться вопросом, почему вы поступали именно так, или, иначе, что именно привело вас к определенным выводам. Проще говоря, вы можете задаться вопросом о том, что именно вы делали. И тогда в качестве ответа вы получите, что вы действовали на основании следующих правил:
1. Мы с вами видели, что сначала мы исходили из дизъюнкции А в качестве истинного выражения. Первое, что мы сделали, это определились с тем, что для того, чтобы доказать тождественную истинность, то есть истинность для любых наборов истинностных значений переменных высказываний, входящих в выражение S, мы начали испытывать все принятые допущения, входящие в А, требуя, чтобы S для всех них оставалось истинным. Это - инстинктивный стереотип. И на основании рассмотрения содержания этого инстинкта мы можем сделать вывод, что множество сделанных допущений выражаются, по крайней мере, в частном случае, посредством дизъюнкции.
Отсюда получаем инстинктивный вывод, что если в высказывании мы имеем дело с множеством допущений, то для доказательства истинности высказывания мы должны испытать на истинность его каждое из допущений. Если для хотя бы одного из допущений высказывание окажется ложным, то оно не будет тождественно-истинным. ;
За любыми словами стоит какая-то реальность, онтологическая или фантастическая. Если мы хотим определиться с качеством высказывания, мы должны обратиться к той реальности, которую мы непроизвольно задали в нём. И когда мы проявим реальность, которая заложена в высказывании, мы сможем эту реальность высказывания сравнить с той реальностью, по отношению к которой строилось наше высказывание, и на основании сравнения придем к выводу, соответствует ли построенное нами высказывание реальности, или же оно представляет собой единственно реальность нашей собственной фантазии.
Итак, высказывание определяется стоящей за ним реальностью. Какого рода реальность стоит за сделанным рассуждением? Это реальность, выражающая отношения между событиями: если есть событие Х, то есть событие В, и если есть событие Y&Z, то есть событие В. События Х и Y&Z рассматриваются в качестве независимых друг от друга.
2. Т.о., мы начали отдельно брать и испытывать каждый из членов дизъюнкции путем осуществления построения истинных дизъюнкций на основании истинности какого-то их члена. А это выражается Правилами введения дизъюнкции на основании её определения: "Дизъюнкция истинна, когда истинен хотя бы один из её членов". Отсюда непосредственно следует обратное отношение: если истинен один из членов дизъюнкции, то истинна дизъюнкция, то есть из А выводимо AVB и ВVA. Если обозначим признак выводимости значком ►, то получим два правила: А►АVB и A►BVA. Безразличие порядка в правиле истинного и присоединенногоо члена дизъюнкции также следует из определения дизъюнкции, в котором говорится об истинности хотя бы одного её члена, то есть указывается на безразличие порядка расположения истинного члена в дизъюнкции и членов, истинность которых для истинности дизъюнкции уже не имеет значения.
Отсюда также общее положение: Определение дизъюнкции (очевидно, как и всякого логического оператора логики высказываний)- это смысл понятия дизъюнкции (соответственно, логического оператора, определение которого задается). Переход от задания смысла оператора как его определения к его формальному выражению представляет собой способ формализации смысла, то есть если смысл оператора рассматривать как его содержание, то формализация смысла есть оформление его содержания, порождающее его (содержания) форму выражения.
3. Второе применяемое инстинктивное отношение связано с конъюнкций (союз "и"), определение которой гласит: конъюнкция истинна, если истинны все входящие в неё члены. Их этого определения получаем правило удаления конъюнкции А&B=A,B и правило введения конъюнкции: А,В=А&В, которые мы применяли в процессе доказательства, "не зная того, что мы делаем".
Всё доказательство может быть представлено в виде дерева::
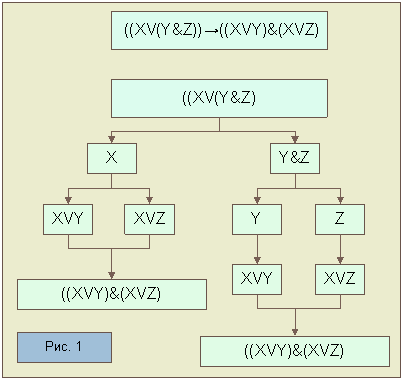
Докажем обратную формулу S-1 = B→A = (((XVY)&(XVZ))→(XV(Y&Z))) на основании дерева рис. 1. У нас две ветви формулы А. Поступим точно также, как мы поступаем при ремонте автомобиля: после того, как какая-то деталь разобрана, мы собираем её в обратном порядке. Начнем с конца первой ветви. Она есть результат введения конъюнкции. Переход на высший уровень дерева получается посредством её удаления. Получаются два дизъюнктивных члена. По отношению к вышестоящему уровню они представляют собой введение дизъюнкции путем присоединения членов Y и Z, поэтому присоединенные члены мы можем спокойно отбросить и т.о. получим Х..
Затем обращаемся ко второй ветви. Её конечный член получен посредством правила введения конъюнкции. Поэтому применяем противоположное правило - удаления конъюнкции и получаем два дизъюнктивных члена, которые получены посредством правила введения дизъюнкции. Присоединенным членом в обоих дизъюнктивных членах является Х. Отбросив его в обоих дизъюнктивных членах, получаем Y и Z, которые, в свою очередь, получены в результате правила удаления конъюнкции. Применяем противоположное правило - введения конъюнкции. Начальный член дерева представляет собой множество допущений, на нижнем по отношению к которому уровне мы имеем дело со списком этого множества. Поэтому мы можем элементы этого списка объединить посредством оператора дизъюнкции и получаем А.
Докажем эту же формулу на содержательном уровне. Удалив из В конъюнкцию, мы получаем две дизъюнкции с одним общим членом и вторыми разными членами. Слушаем, что говорит нам наш инстинкт. Инстинкт говорит нам о том, что возможно "склеивание" общего, поскольку истинностное значение Х в обоих дизъюнкциях одинаково. Так как дизъюнкция - это набор допущений, то мы можем рассматривать Х в качестве допущения, из которого должно быть получено А. Действительно, посредством правила введения дизъюнкции из Х мы получаем (XV(Y&Z)). У нас остаются в качестве членов дизъюнкций Y,Z, каждое из которых должно быть испытано. Но формула А может быть получена только из их конъюнкции, поэтому мы должны требовать истинности их обоих, то есть должны объединить их конъюнкцией. Тогда, имея конъюнкцию, применив правило введения дизъюнкции, мы получаем А.
4. Когда речь идет об обратных доказательствах, то речь идет о наличии симметричных обратных операций, под которыми понимаются операции вывода, справедливые "сверху вниз" и "снизу вверх", то есть в которых вывод и заключение могут непосредственно меняться местами. относительно тех, которые были применены при прямых доказательствах. В случае же, подобного дизъюнкции, которая не имеет обратной симметричной операции, должны применяться "соответствующие приспособительные методы", подобные тем, которые были применены к дизъюнкции, трактуемой в содержательном аспекте как совокупность допущений, так что для каждого из допущений следовало строить свои доказательства. То есть мы тем самым доказываем множество формул и затем объединяем их в одно выражение: X→XVY, XVZ→(XVY)&(XVZ) (1), т.е. X→(XVY)&(XVZ). Рассматривая генезис доказательства (1), мы можем на основании его содержательного рассмотрения получить Х, но мы не докажем Y&Z, поскольку они являются присоединенными членами. Как и обратно, мы можем из Y&Z доказать А, но из А мы не докажем Х. Т.о., формула S является сложной, "синтетической" формулой, состоящей из множества независимых друг от друга входящих в ней формул.
5. Есть особенность: то, что представляется само собой разумеющимся, начинают доказывать, и в результате чего дело запутывается. Вообще обычно то, что представляется очевидным, обычно принадлежит нашему инстинкту, отражению реальности, поскольку только отражене реальности может быть очевидным или кажущимся.
стр.17 Второй пример. ((ᴧxᴠyFxy)→(ᴠyᴧxFxy) (1) (Г.—А., формула 36, стр. 107). Будем рассуждать так: существует такой х, что для всякого у справедливо Fxy. Пусть а — один из таких х. Следовательно, для всех у имеет место Fay. Пусть Ь — некоторый произвольный объект. Тогда имеет место Fab. Итак, существует некоторый х, а именно а, такой, что имеет место Fxb. Так как b любое, то это имеет место для всех объектов, т. е. для любого у существует некоторый х такой, что имеет место Fxy. Этим рассматриваемое утверждение доказано.Данная формула сводится к порядку применения операторов кванторов и общности.
Высказывания характеризуются тем, что это - высказывание относительно чего-то, что выступает в качестве субъекта. Следует различать высказывания от функции, которая представляет собой неявную форму высказывания. Например, функция вида Fxy представляет собой два высказывания: высказывание относительно х и высказывание относительно у. Например, Если А выражает предикат "Больше", то F(x,y) = x>y = y<x. Другими словами, мы можем задать какое угодно отношение от какого угодно числа переменных. Однако требование, которое мы обязаны предъявить к высказыванию, это то, относительно чего в функции высказывания идет речь, то есть относительно чего делается некоторое утверждение и что именно относительно него утверждается. В этом смысле принятое понятие высказывания как такого, чему приписывается определенное истинностное значение (обычно высказывание произнесено, и ему автоматически приписывается истинностное значение истина. Не говорят, что А есть истина, или А истинно, а просто говорят А. Чем различаются части формулы (1)? Тем, что в этой формуле в качестве субъектов высказывания выступают различные объекты. Рассмотрим такие высказывания: "Иван передал вещь Петру" высказывание отвечает на вопрос "Кто передал вещь Петру" "Вещь была передана Петру Иваном"-что было передано Петру Иваном? Петр получил вещь от Ивана" -Кто получил вещь от Ивана. В качестве субъекта высказывания выступает ответ на вопрос. Т.о., для определения субъекта высказывания необходимо установить, на какой вопрос отвечает высказывание. Но: можно задать вопрос: "Кто передал вещь Петру?" На место "кто" подставляем ответ. Получаем: "Иван передал ведь Петру" Но мы можем также задать вопрос: "Кем была передана вещь Петру?"- и получим ответ: "Вещь была передана Петру Иваном". Здесь "Иван" выступает в качестве средства. Формально подлежащим высказывания является вещь, поскольку относительно неё утверждается нечто, а именно, что она была передана и т.д. Однако высказывание "Вещь была передана Иваном" отвечает на вопрос "что было сделано с вещью", и тогда возникает вопрос о переходе от пассивной формы сообщения к активной, а это уже вопрос "кто передал вещь?" Т.о., связь между активным и пассивным оборотами связана с объектом, который действует и объектом, на который направлено действие или с которым осуществляется действие, что одно и то же. Поэтому необходимо делать различия между пассивными и активными оборотами.
C логикой предикатов возникают вопросы, когда мы обращаемся к общеязыковой практике, а также практике математической. В языке мы имеем дело с суждениями, субъектом которых является множество объектов (элементов), относительно которых нечто утверждается или которые нечто утверждают, в качестве предиката выступает то, что именно утверждается об объектах. В логике предикатов мы имеем две формы: Р(х) и R(x,y,...,). Но R выражает отношения. И в таком случае мы должны говорить о логиках двух типов - логике предикатов и логике отношений. Сейчас же также и R рассматривается в качестве предиката, то есть некоторого утверждения, которое выражает отношения между множествами объектов. Далее, если существует логика предикатов, то должна существовать и логика субъектов, если уж на то пошло.
Далее, формы Р(х) и R(x,y,...,) представляют собой подражание математическим выражения. Но среди математических выражений мы встречаемся с неявным заданием функции F(x,y,...) и её явным заданием: x=F(y,...), y=F(x,...) и т.п. Между тем, в логике предикатов этого нет. Понятно, что задаются подстановки из области определения объектных переменных, и в результате этого получаем высказывание с его истинностным значением. То есть мы можем написать Р(х)=з, где з - истинностное значение, такое, что з=и, л (истина, ложь)
Для чего делаются утверждения
В логике вообще имеют дело с утверждениями, и одни из них являются положительными, другие - отрицательными, одни из них являются общими, другие - частными, третьи - единичными, и все эти утверждения характеризуются в качестве истинных или ложных. Это общее свойство всех утверждений важно: субъект делает утверждение и объявляет его истинным. То же, истинно оно на самом деле или нет - это уже другой вопрос. Поскольку субъект некоторое своё утверждение объявил истинным, он, если он логичен, должен в своей практике следовать ему, и это его следование своему утверждению имеет для субъекта, а также реальности, относительно которой он сделал утверждение, последствия. И тут мы увидим, что утверждения человека, которые он делает, определяются практическими последствиями, которые возникают для него в результате следования утверждениям. В связи с этим можно ответить на вопрос: для чего, с какой целью делаются утверждения? - для того, чтобы следовать им (или же для того, чтобы им следовали те, которые их принимают в качестве истинных). В этом заключается функция утверждений и функция всех высказываний, которые делает человек. Любое высказывание имеет свою цель, которой оно должно удовлетворять.
Но этим же должен определяться также и подход к исследованию того, для чего делаются те или иные высказывания. Если цель, ради которой делалось высказывание и благодаря следованию ему цель была реализована, то высказывание принимается в качестве истинного, если же нет - то высказывание является ложным и нуждается. в лучшем случае в коррекции.
В таком случае утверждение не может рассматриваться само по себе. Оно выступает в качестве программы, определяющей реализацию цели. Поэтому по большому счету нельзя брать высказывание само по себе.
Следующий момент: человек в своей деятельности использует категории "хорошо" и "плохо". То, что хорошо, принимается им в качестве истинного, то, что плохо - в качестве ложного. То же относительно "прекрасного" и "уродливого".
Форма неявного задания функции представляет собой неявный предикат. Неявный предикат должен быть преобразован в явный для того, чтобы он мог стать высказыванием. То есть он должен представлять собой некоторое суждение, то есть то, что обладает субъектом и предикатом.
74. С высказыванием связано понятие информации.
75. Одна и та же функция в зависимости от ответа на вопрос сообщает разную информацию. Вторая мысль – должны быть заданы области определения любого высказывания.
76. Признаки, при посредстве которых выделяются объекты, можно рассматривать в качестве дерева, на вершине которого находятся самые общие признаки, и дальше по ветвям – специфические признаки. Т.о., когда речь идет от опыте действий с объектом, то вначале всё множество объектов некоторого рода выступает на одно лицо.
77. Итак, это – признаки, на основании которых объекты выделяются: специфические отличия их форм, а также цвета, запаха и т.д. Но объекты нас интересуют в связи с их функциональностью – какого рода потребности наши они способны удовлетворять или какого рода вред они могут нам причинить.
. Правила вывода из Генцена. (1)
Разбор случаев: Генцен: OB («разбор случаев»). "Если доказано А V В, то можно вести доказательство разбором случаев. Предположим сначала, что имеет место А, и из него выведем С. Если далее из предположения о том, что имеет место В, снова вывели С, то С вообще имеет место уже независимо от обоих допущений (ср.21)." Но этому правилу доказательства соответствует формула: АvB→C ≡ (А→С)&(B→C)
Что здесь важно: Важен переход от формулы сначала к правилу доказательства и затем к практическим, по сути своей содержательным действиям, которые связаны с применением этих правил.
7. Правило вывода лⱵА Из лжи следует что угодно. Другими словами, это - правило антидетерминизма, правило введения чуда: ведь понятие чуда как раз и предполагает ожидание чего угодно. Что такое ложное высказывание? Это относительно реального положения вещей какое угодно высказывание. Достоевский: врем, врем, и, может быть, довремся до правды. Из лжи следует что угодно означает, что из лжи может следовать как правда, так и ложь. Другими словами, если вы имеете дело с лжецом, то из того, что он говорит, может следовать что угодно.