Действие и восприятие - противоположности. Вспомните о сороконожке, которая не смогла ходить, как только задумалась о том, как она ходит. Когда мы что-то делаем, мы руководствуемся бессознательным, или интуицией, или инстинктом, это уж кому какое название больше нравится. При этом у нас есть ощущение, что мы делаем именно то, что нужно, но при этом мы не знаем, почему мы делаем так или иначе. В процессе действий у нас может возникнуть ощущение, что мы отклонились от правильного пути. Наконец, у нас может возникнуть ощущение, что движение по ветви пути, по которой мы идем, исчерпало себя, и мы представления не имеем, куда мы могли бы двигаться дальше. Мы ощущаем, что зашли в тупик.
Но после
того, как мы что-то сделали, мы можем задаться вопросом, что же такое мы делали
и что мы получили в результате, если, конечно, вообще получили что-н. Мы
объективируемся по отношению к тому, что делали, процесс действия исчезает в
своих результатах, превращается в них вещь, следовательно, в то то,
что существует параллельно во всех своих частях. И тогда относительно
полученной вещи мы можем задаваться вопросами, почему, с какой целью мы
нечто делали и какие функции в целом представляет собой каждая из его частей
. Но также и объективированное рассмотрение вещи не может
рассматриваться иначе, как только
в какой-то последовательности.
То, что такой вещью является текст, ничего не меняет требованиях ответа на
вопросы, для чего, для какой цели предпринималось то или иное действие,
вылившееся в тот или иной текст. Наконец, естественно, что самое важное во
всём этом - это конечная цель действия.
Здесь
присутствует одна запятая, которая заключается в инстинктивном ощущении, что
целью действия является то, что мы получили в конце. Например, если нам нужно
купить хлеб, то для этого мы должны совершить ряд действий: взять деньги, пойти
в магазин и прочее. Но конечная цель - это хлеб. Действия могут быть разными, но
цель - одна. Однако когда у Шолохова спросили, что он хотел сказать своим
романом "Тихий Дон", он ответил: всё то, что написано. Другими словами, каждая
из частей романа имеет значение, и целое представлено всем текстом романа, а не
какой-то его частью.
Поэтому, если мы хотим узнать, что
же такое мы сделали, мы должны ответить на вопрос: а для чего у нас в тексте
существует та или другая его часть. И ответить на этот вопрос оказывается не
просто, потому что для этого нужно держать в голове такого рода целое, части
которого, как тараканы, пытаются разбежаться в разные стороны.
Вот, например, в статье 1 задается таблица логических операторов. А для чего, собственно? Потом идет речь о возможных отношениях между множествами. Ну, и "нехай". И далее речь идет о графо-аналитическом представлении множеств. Вводятся обозначения, понятие универсального множества, элемента, виды отношений между множествами - включения класса в класс и т.п. Ага, это, значит, для того, чтобы можно было говорить о множествах. Тогда и таблица бинарных операторов с названиями последних также введена с этой целью. Хорошо, это - понятно. Хорошо, плохо ли это сделано, но как-нибудь да сделано. Что мы видим? Мы видим, что делается нечто целое из таблицы операторов и отношений множеств. А затем это целое разбивается на части. То есть мы от целого, леса, переходим к деревьям, что ведет к риску того, что мы за деревьями перестанем видеть лес. Для чего у нас эти две части, таблица операторов с описывающими её понятиями и понятия, описывающие отношения множеств, понятно: ими формируется возможность делать высказывания как относительно одного, так и другого предмета.
А далее
уже идут сами действия с объектами. Что же это за действия? Мы начинаем с того,
что задается какое-то отношение множеств, например, А=В. Относительно этого
отношения выясняется, какими свойствами его элементы обладают, и
какими - не обладают. И выясняется, что они обладают свойствами А,В и -А,-В и не
могут обладать свойствами -А,В, А,-В
После этого совершается
качественный скачок - переход от чувственного уровня к словесному, на основе
принципа параллелизма чувственной в виде отношений множество и словесной,
описывающей эти отношения, реальности. Значит, то, что делается на этом
этапе, это переход от непосредственного чувственно-практического уровня к уровню
языковому.
Как это делается? На место множества
подставляется высказывание о нём. Знак, которым непосредственно обозначается
множество, отождествляется с высказыванием, представляющим множество.
Другими словами, множество как чувственная данность и его знак, с одной стороны,
и тот же самый знак и слово (звук,, набор звуков), которым этот знак выражается
в виде высказывания, представляют собой опосредованное отношение двух "крайних
терминов" - множества и выражающего его слова через посредство среднего термина
- знака. Крайние термины различаются т.о., что множество как таковое - это образ
чувственной реальности, слово - представляет понятие. Этим, по идее,
и обеспечивается переход от чувственной реальности к выражающей его речи, как и
обратно, от понятия, выражаемого в речи - к чувственной реальности как
соответствующей этому понятию. Т.о. через опосредующую роль общего знака,
обозначающего как множество как чувственную данность, так и высказывания как
представителя сферы мышления устанавливается связь между этими двумя
реальностями - реальностью чувства и реальностью мышления.
Т.о. происходит переход к высказываниям и, соответственно, к истинностной
таблице бинарных операторов, так как высказывания принимают значения
"истина","ложь".
Как
выражается отношение множеств в речи? В речи отражаются отношения между
множествами не абстрактно, а через высказывания, которые выражают отношение
одного множества к другому, так что при этом одно множество выступает в качестве
субъекта, другое - предиката.
. Должно быть дано описание всех
логических возможностей, а не одной или двух. Тогда мы получим
полную информацию относительно свойств объектов, то есть отношений между
множествами. И при этом важно выделение множества, по отношению к которым
рассматривается другое множество.
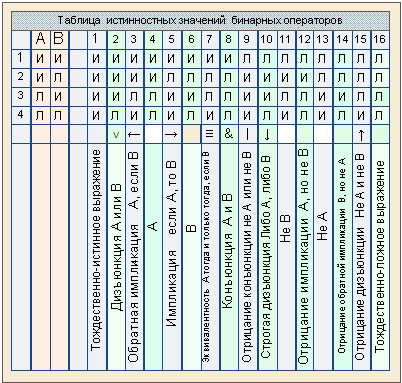
Произведем такой опыт. Пусть дано АTВ. Рассмотрим
отношения А/В (А к В), А/-В, -А/В, -А/-В Получим следующие суждения:
˄х(хϵА→хϵВ)
= и, ˅х(хϵА→хϵ-В)=л,
˅х(хϵ-А→хϵВ)=и,
˅х(хϵ-А→хϵ-В)=и.
Последовательность высказываний соответствует последовательности строк
истинностных значений переменных А,В таблицы бинарных операторов. На
основании полученных высказываний можем сделать вывод, что если истинно
одно высказывание (первая строка), и ложно второе высказывание (вторая строка),
то первое высказывание является общим. Если же и одно (третья строка
таблицы) и второе (четвертая строка таблицы) являются оба истинными, то оба
высказывания являются частными (правило (1)).
Проверим, насколько работает это правило. Рассмотрим отношения В/А, В/-А, -В/А,
-В/-А. Так как В у нас на этот раз выступает уже не в качестве предиката, а в
качестве субъекта, то мы должны в таблице истинности переставить А и В местами.
Хотя можем и воспользоваться существующей последовательностью А и В, памятуя,
что при этом идем не от А к В, а от В к А. Получаем:
˅х(хϵВ→хϵА)=и,
˅х(хϵВ→хϵ-А)=и,
˄х(хϵ-В→хϵА)=л,
˄х(хϵ-В→хϵ-А)=и.
Это - набор истинностных значений иили какого-то оператора. Этому набору
соответствует оператор обратной импликации и мы видим, что
относительно него выполняется правило (1) отсюда , обобщая, делаем общий
вывод, что на основании знания оператора высказывания мы можем судить о
том, какого рода суждениями характеризуются отношения между множествами, и, в
силу этого, вместо того, чтобы записывать множество высказываний с
кванторами, достаточно просто записать выражение с оператором, например для
рассматриваемого случая отношения включения множества А в В АTВ.
записать А→В.
( Примечание: в логике высказываний
операторы импликации и обратной импликации и отношения включения множества в
множество часто обозначаются одинаковыми знаками V,
T
однако противоположным образом, то есть включению множества А в В АTВ
соответствует импликативное высказывание АVВ, и
обратно.)
Непосредственно отсюда нами
получается противоположный вид задачи: определить, какого рода отношения между
множествами выражает тот или иной оператор.
После того, как сформулировано правило определения
оператора высказывания по заданному отношению между множествами, решение задачи
для произвольного отношения между множествами представляет собой уже сугубо
техническую задачу и не представляет интереса. И именно отсутствием интереса и
объясняется ощущение тупика, в который мы попали. Выход на противоположную
задачу и есть выход из тупика.
Что же обеспечило выход из
тупика? Реализация цели. Целью было найти правило, в соответствии с которым
можно перейти от чувственно заданных отношений между множествами к выражению
этих отношений в логических формах речи. Но как раз формулировка правила (1)
перевернула отношения и позволила перейти к противоположной задаче - определению
отношений между множествами по их выражению в логике языка. Случайность ли это?
Вспомните маленький отрывок из статьи 1 относительно рефлекса как механизма
преобразования последовательного во времени отражения действительности в
опережающее её отражение, когда сформированный рефлекс оборачивается и уже
заранее, на основании существующей потребности, проецирует образы, которые
являются исходным пунктом для удовлетворения рефлекторной потребности. Это
значит, что реализованная цель превращается в средство
реализации
последующих целей.
Следовательно, бесконечный прогресс
познания представляет собой диалектику средства и цели: цель формируется на
основе существующих средств. Средства есть результат
материализованных целей.
27.09.11 г.