Логика и реальностьАнатомия формулы Sn3
Найти сумму первых n кубов натурального ряда чисел.
В форме
n3/3 + n2/2+n1/6
мы наблюдаем следующие особенности: в первом и во втором слагаемых
выражения числа в степени и в знаменателе равны. В третьем слагаемом
знаменатель равен произведению степеней n. Поэтому мы можем предположить,
что для суммы кубических степеней элементов натурального ряда будет
справедливо выражение Sn3=n4/4
+ n3/3 + n2/2+n1/24
(1), как вообще верна формула Snk=nk-1/(k-1)
+nk-2/(k-2) + n3/3
+ n2/2+n1/((k-1)(k-2)...3*2*1)
(2). Однако проверка формулы (1), не говоря уже о формуле 2,
показывает, что сделанное обобщение не работает. Поэтому обратимся к более
общей форме Sn3=n4/a
+ n3/b + n2/c+n1/d
и посмотрим, работает ли она для кубов натурального ряда.
Строим таблицу:
n 1 2 3
4 5
6
n3 1 8
27 64 125 216
Sn3
1 9 36 100 225
441
√ 1 3 6
10 15 21
-
2 3 4
5 6 |
Исходим из алгоритма, примененного в предыдущей главе. Тетраконтейнер
n4 = 256. Sn3=100.
В тетраконтейнер входят 4 кубических контейнера, в каждом из которых
находится 4 квадратных контейнера, содержащих по 4 линейных контейнера по 4
элемента в каждом. Т.о. в одном квадратном контейнере находится 16
элементов, в одном кубическом контейнере находится 64 элемента. Т.о., мы
можем разделить 216 элементов на четыре и получим один полный кубический
контейнер и нам останется определиться с 36 элементами.
Кубический контейнер содержит 64 элемента: 4 квадратных контейнера по
16 элементов в каждом. Делим кубический контейнер на 2 и получаем
два полный квадратных контейнера. Берем квадратный контейнер. Он состоит из
четырех линейных контейнеров по 4. Все элементы исчерпаны. Получили:
Sn3=n4/4
+ n3/2 + n2/4
(3)
Докажем методом математической индукции правильность формулы
(3).
Для n+1 члена из (3) получаем:
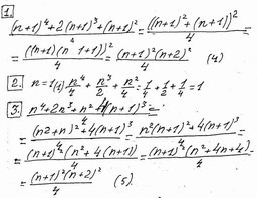 (4)=(5), ч.т.д.
(4)=(5), ч.т.д. Найти сумму
первых n элементов четвертой степени натурального ряда.
Применим
два рассуждения методом контейнеров, одно рассуждение неправильное и другое
правильное с тем, чтобы прояснить, что можно делать в правиле контейнеров, и
чего нельзя.
Первое рассуждение.
Первый способ
рассуждения заключается в том, чтобы делить контейнер на максимальные части,
переходя к целым частным от деления.
Второе рассуждение
Второй способ рассуждения заключается в том, чтобы брать максимально
возможные части контейнера, невзирая на появляющиеся части элементов.
При рассмотрении квадратных контейнеров вопрос о противоположностях и о
"серых элементах" представляется ясным. Но что происходит с
противоположностями при переходе к кубу? Как в этом случае распределяются
противоположности? что возникает в этом случае - удвоение, утроение? что?
Возвратимся к рассмотрению выражений с квадратным контейнером и к рис.1:

Что такое голубое? - это сумма предшествующих членов. Что такое серое -
это число элементов последующего члена. n2
- это удвоенная сумма предыдущих членов плюс один последующий член.
Следовательно, если мы добавим последующий член, то получим две удвоенных
суммы и, т.о. (n2 + n)/2 даёт нам сумму.
Сравним выражения n2
(1) и n2+ n (2)=n(n+1)(3).
Пусть n=3, тогда n2=9;
(n+1)(n+1)=4*4=16. Но n(n+1)=3*4=12.
Разность 16-9=7=3+4. Т.о. (3) представляет собой прямоугольник, который
образован линейными контейнерами: три контейнера по 4 элемента либо 4
контейнера по три элемента. Если берем квадратный контейнер 4 по 3, то
получаем n2 = 32+3,
если берем 3 по 4, то получаем 42 - 4.
Количество элементов одинаковое, но смысл их получения противоположный.
n2+n=(n+1)2
- (n+1)
Самая первая мысль, которая приходит, это преобразование
прямоугольников в квадраты. Посмотрим, как это можно сделать и какие новые
понятия в результате этого получаются.
В треугольнике на рис. 1 слева
направо мы имеем столбцы, содержащие элементы натурального ряда. В качестве
таких элементов могут выступать элементы каких угодно рядов, например,
квадратов натурального ряда. Для всякого фиксированного n мы можем получить
соответствующий треугольник, содержащий сумму элементов. Если мы удвоим эту
сумму, то квадрата не получим, нам придется добавлять к этой сумме
число до ближайшего квадрата. Так, . 2Sn=5
=2*15=30 - это не целочисленный квадрат. Мы можем добавить 6 элементов, и
тогда получим число 36 и можем всё это дело представить в виде квадрата.
Т.о., чтобы получить сумму первых n членов натурального ряда нам нужно взять
квадрат (n +1), вычесть из полученного результата (n+1) и разделить
полученный результат на 2. Например, пусть n=8. Тогда 81-9=72/2=36. Т.о.
Sn=((n+1)2
- (n+1))/2 (4)=n(n+1)/2 (5) Формула (4) проявляет смысл того, что
выражает формула (5)
|

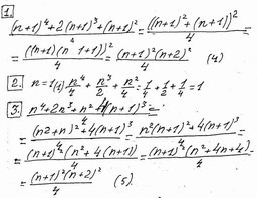 (4)=(5), ч.т.д.
(4)=(5), ч.т.д.