Представление дерева
Два способа представления материала: можно говорить об объекте - и
можно представлять объект и через посредство представления иметь дело
с (чувственным) образом объекта как с (феноменологической) реальностью.
Если то и другое, то тем самым обеспечиваются обе стороны отражения:
чувственного восприятия и рационального обсуждения.
Дерево.
Для того, чтобы представить дерево чувству, можно нарисовать его
экземпляр. Но это будет конкретное дерево. Если же мы хотим говорить о
классе различных деревьев, то должны ввести обозначения для компонентов
дерева и говорить о дереве посредством введенных обозначений. При этом
можно идти от рисунка дерева, обозначая его части, или от представления
дерева, которое содержит в себе различные части, которые как-то
обозначаются. Можно начать с описания представления дерева и затем идти
к обозначениям его частей с тем, чтобы затем можно было представлять
дерево в математической форме.
Обычно одни понятия определяются через другие. Но в
конечном счете приходят к объектам, которые не определяются через другие
понятия. На такие объекты нужно просто указать. В данном случае это
понятия узла и ветви дерева. Иначе можно сказать, что узел дерева
представляется
точкой, ветвь дерева - отрезком прямой. Это - как представляемые,
так и чувственно воспринимаемые объекты, если они обозначены на
бумаге.
Но это - не реальные чувственные объекты, обладающие телом, хотя у нас
и существует стремление относиться к ним как к таковым. Это
- знаки, которые представляют не себя, а что-то другое. Однако эти знаки
обладают свойством, которым не обладают чувственные объекты,
именно, мы можем создавать какие угодно знаки, какие угодно их
интерпретации, какие угодно правила оперирования с ними. Знаки, тем не
менее, несмотря на наши усилия, не полагают, а предполагают нечто: за
знаками мы видим нечто иное, некоторое мыслимое или немыслимое
содержание, представителем и указателем на которое они являются. В этом
смысле знаки могут рассматриваться как материальные формы
соответствующего содержания.
Дерево состоит из
множества узлов и ветвей. Каждый узел дерева характеризуется тем, что
либо не имеет , либо, если имеет, то только одну входящую входящую в
узел ветвь, и ни одной или множество исходящих из него ветвей. Если в
узел не входит ни одна ветвь, то узел называется вершиной дерева. Если
из узла не выходит ни одна ветвь, то узел называется конечным или листом
дерева, если узел представляет чувственный ("телесный") образ.
Дерево содержит в себе множество путей от вершины к конечным узлам,
равное их числу. Путь от вершины дерева до его конечного узла является
единственным потому, что в каждый из узлов дерева входит единственная
ветвь и два пути различаются по крайней мере одной ветвью. Если бы в
узел дерева могло входить более одной ветви, то в один узел могли бы
входить разные ветви от разных узлов. А это был бы уже не один путь.
Итак, признаком единственности пути является вхождение в узел дерева
единственной ветви.
Пусть имеем узел листа. В
лист входит одна ветвь. Всякая ветвь характеризуется тем, что она
выходит из какого-то узла и входит в какой-то узел. Если ветвь входит в
некоторый узел, то она выходит из единственного узла. Поэтому имеет
место однозначное, но не одно-однозначное соответствие между двумя
узлами, соединенными ветвью, именно, листу соответствует один узел, но
обратное неверно, так как породившему лист узлу может соответствовать
любое множество порожденных им узлов. Так как это правило выполняется
для всех без исключения ветвей, то между вершиной дерева и его листом
существует единственный путь.
Уровни дерева. Узел дерева, рассматриваемый по отношению к
входящей в него ветви, называется порожденным, рассматриваемый по
отношению к выходящим из него ветвей, называется порождающим. Т.о.,
каждый узел может быть только порождающим (вершина), только порожденным
(конечный узел) либо порожденным и порождающим. Под уровнем дерева
понимается множество узлов дерева, путь к которым содержит
одинаковое число ветвей (соответственно, одинаковое число порождающих
узлов. Уровни считаются от вершины дерева.
Примечание.
Обычно считается, что человек идет от чувственной реальности и строит
свои представления в соответствии с чувственной реальностью. На практике,
однако, человек подводит чувственные данные под свои представления, которые
уже существуют у него. Если же ему не удается это сделать, то он начинает
строить представления, опираясь на чувственные данные как на
образец, отдельный пример соответствующего класса представлений.
Следовательно1, представление не является
простым фотографическим снимком чувственных данных. Представление строится
человеком точно также, как он строит дом - посредством активной деятельности,
различие же состоит в том, что представление он строит посредством своей
интеллектуальной, дом - физической деятельности.
---------------------------
1. Всякое "следовательно" строится на основе
закона тождества: в выводе повторяется то, что уже содержится в неявном виде в
посылках. В этом смысле вывод делает явным неявное, то есть делает субъектом
суждения нечто, содержащееся в чем-то в качестве его предиката.
Строим представление дерева
Обозначим число уровней дерева D
индексом n: Dn.1
Задача, которая возникает при этом перед человеком - это обозначение
посредством системы знаков соответствующей произведенной человеком
интеллектуальной чувственной реальности. В настоящем случае такой задачей
является представление в знаках дерева как в абстрактной, знаковой его
форме, так и в конкретной, чувственной форме, представляющей собой рисунок
отдельного дерева.
В выражении Dn
xисло n обозначает наиболее
длинный путь дерева, где под путем дерева понимается цепочка узлов,
последовательно соединенных ветвями от вершины конечного узла
дерева2.
Всякое обобщение связано с отрывом от некоторой конкретной чувственной
данности, которая может рассматриваться в качестве примера класса
соответствующих объектов. Построим такой пример воображаемой чувственной
данности в виде дерева, из вершины которого выходят три ветви, заканчивающиеся
тремя узлами, и каждый из этих узлов, в свою очередь, порождает по три ветви, в
свою очередь заканчивающиеся тремя узлами. Далее мы можем сделать первое
обобщение, сказав, что далее дерево ветвится в соответствии с заданной
закономерностью, которая может быть сформулирована т.о., что каждый узел дерева
порождает три ветви, заканчивающиеся узлами. Мы можем ограничить этот процесс,
задав n уровней дерева.3 Обозначим вершину
дерева а1, второй уровень - а2, третий уровень - а3 и т.д., Пусть
дерево имеет n уровней. Тогда можно записать.: Dn
= a1,a2,... ,an = П1...i...nai,
где i=1,...,n обозначает уровень дерева, n - число уровней.
Каждый уровень дерева содержит какое-то количество узлов. Если уровни дерева
представить (записать) в столбец, то узлы уровня дерева могут быть
записаны в виде строк, соответствующих уровням дерева, и тогда, перенумеровав
узлы уровня слева направо, мы можем рассматривать значения номеров узлов уровня
в качестве их адресов, и тогда всякий узел дерева может быть записан в виде Dij,
где i - уровень дерева, в который входит узел,
j-адрес узла в уровне.
Однако, так как узел
последующего уровня порождается узлом предыдущего, то в данной записи адресов
узлов это ключевое обстоятельство не отражается. Правда, это обстоятельство не
может помешать нам обозначить любой возможный путь дерева на основе следующего
соглашения: примем, что уровни дерева обозначаются строчно слева направо,
начиная с вершины. Тогда уровни дерева запишутся как 1,2,
... , n. Будем считать, что каждая цифра обозначает место, в которое
записывается адрес узла уровня, которому принадлежит соответствующее место.
Тогда выражением 127 будет представлена последовательная адресация узлов одного
из путей дерева. Обозначая соответствующие места переменными, например, a,b,c,
... , и придавая значения переменным, кажется, что мы в неявном виде зададим всё
дерево, однако это не так, поскольку в этом случае для того, чтобы задать тот
или иной путь, нам нужно уже иметь дерево в качестве чувственно заданного, что
связано с отсутствием данных переходов от предыдущего уровня к последующему.
Например, из принятого соглашения мы можем задать адрес 121, что не будет
соответствовать дереву, которое мы взяли в качестве примера.
Если употребляется термин адреса узла,
то это требует формулирования правил
адресации. Будем считать, что 1. Всё множество узлов произвольного уровня
делится на множество подмножеств, каждое из которых порождено одним из узлов
вышестоящего уровня. Число таких подмножеств равно или меньше (если некоторые
узлы в нём являются конечными) числу узлов вышестоящего
уровня. Адресом подмножества является адрес породившего его узла
вышестоящего уровня. 2. Множество узлов каждого из подмножеств
пересчитывается отдельно, и каждому узлу подмножества ставится в соответствие
номер его счета. Тогда число узлов равно максимальному значению адреса N{y}=Amax(y)
(Мощность множества {у} равна максимальному адресу) 3. Этим определяется принцип
формирования записи адреса произвольного узла, требующий последовательного
указания адресов узлов, начиная с верхнего уровня и кончая последним, чем и
определяется путь к узлу от вершины дерева. Например, выражение D513734
может выражать путь от вершины дерева до одного из его конечных узлов.
Можно получить информацию не только о пути, но и частичную информацию о дереве,
приписав в качестве индекса каждому адресу узла максимальный адрес, то
есть общее число узлов порожденных вышестоящим узлом, например: D51136773444.
Читается это выражение по схеме: читается индекс, указывающий число узлов,
возврат к адресу одного из узлов, переход к индексу следующего разряда числа,
читается адрес узла из данного множества узлов, и т.д. Т.о., число вершин и
адрес вершины = 1, которая породила 6 узлов, в которых третий узел породил 7
узлов, из которых седьмой узел породил четыре узла, из которых третий узел
породил 4 узла, где четвёртый узел является конечным.
В общей форме это может быть выражено сл.о. Допустим, у - переменная,
определенная на множестве узлов дерева. Последовательность индексов при y
a,b,c,d,... обозначает координаты узла т.о., что индекс а соотносится с адресом
узла первого уровня, b - с адресом узла подмножества узлов второго уровня дерева
и т.д. Здесь места, которые занимают буквы, считаемые слева направо,
соответствуют номерам уровней, а значения букв - адресу узла в подмножестве
уровня. Адрес же подмножества уровня определяется адресом породившего его
вышестоящего узла. Тогда получаем адрес узла yabcde...,
который прочитывается сл.о. а =1, так как а - вершина дерева, b - адрес из
множества узлов второго уровня, порожденного единственным узлом верхнего уровня.
с - адрес из подмножества множества узлов третьего уровня, порожденного узлом с
адресом b множества узлов второго уровня. Продолжая эту операцию, мы на каждом
шаге определяем адрес узла последующего уровня дерева, и в целом - также и путь
к этому адресу от вершины. Если наряду с этой схемой адресации узлов
применяется также схема, в которой адреса узлов уровня подсчитываются слева
направо, то, если I - номер уровня, J - адрес ячейки в уровне, то получим: уIJ
= yabcd...,где число мест при у в правой части
уравнения равно I, например, у4J = yabcd
Каждый нижеследующий уровень формируется
множеством функций от множества узлов вышестоящего уровня. Поэтому с
каждым узлом порождающего узлы уровнем соотносится функция порождения
Например, если есть три узла с адресами 1, 2, 3, то им будут соответствовать
порождающие функции f1, f2,
f3. Можно считать, что каждая из порождающих
функций порождает множество упорядоченных узлов, то есть узлов с их адресами.
Тогда с каждым из порожденных узлов в свою очередь соотносится соответствующая
порождающая функция. Порождающая функция преобразует узел в множество
упорядоченных узлов. При этом её результат может быть представлен в виде
упорядоченных узлов либо сокращенно в виде количества производимых ею узлов
Пусть дан узел у1. Тогда f(y1)=
y12, где у12 -
переменная, пробегающая по множеству узлов уровня 2. При этом у нас нет данных о
том, сколько узлов содержит y12. Другое дело,
если нам дан адрес узла, как это сделано выше. По отношению к нему может быть
определена порождающая функция. Поэтому, если мы хотим выразить путь, связав
узлы с функциями, то должна быть задана технология связки двух функций. Пусть
функция от узла дает число порожденных ею элементов и адрес элемента, от
которого берется порождающая функция. Тогда получаем последовательность функций:
f15 → f23f15,
где порождающая функция вершины порождает 5 узлов, следующая функция порождает
из второго порожденного узла 3 новых узла. Применяя эту схему действий, мы
получаем возможность выразить как путь, так и множество порождаемых узлов на
каждом шаге применения функций, где уровень узла определяется местом функции,
подсчитываемым справа налево.
Узлы последующего
уровня связаны с определенными узлами предыдущего.
Неявно уровни выражаются посредством введения
понятия
места уровня. Если мы имеем какое-то число, то каждый из его разрядов
занимает в числе определенное место. Будем считать разряды числа слева направо,
отождествляя первый разряд с вершиной дерева и с первым его уровнем, второй
разряд со вторым уровнем и т.д.
Всюду мы наталкиваемся
на одно и то же: на качественное различие объектов в записи, связанное в одном
случае с адресом узла, в другом - с количеством порождаемых узлов.
Объединить в одном выражении адрес узла и порождаемое им количество узлов можно
посредством дроби, записывая в её числителе адрес узла, в знаменателе - число
порождаемых им узлов. Т.о. числитель представляет вышестоящий, знаменатель -
нижестоящий уровень.
Рассмотрим выражение 1/3,(1/2, 2/5, 3/4)- Узел
первого уровня порождает 3 узла второго уровня. , узел 1 второго уровня
порождает два узла третьего и т.д.. Выражение вида 1/3,(1/2, 2/5, 3/4) может
быть обобщено на произвольное число уровней в виде a/b,b/d,d/e,...=Пn(уi/yi+1)
(1), i= 1...n. В выражении a/b,b/c
b в знаменателе и в числителе дроби выполняет разные функции: в числителе оно
обозначает адрес узла подмножества уровня дерева, в знаменателе оно обозначает
количество узлов нижележащего уровня, которое оно порождает, и, соответственно,
в числителе "у" выступает в роли порядкового числительного, в роли переменной,
которая принимает значения из области, определенной значением "у" в знаменателе,
играющего в знаменателе роль количественного числительного, то есть константы.
Поэтому при построении дерева "у" в числителе в качестве переменной должна
пробегать по всем своим значениям, а не ограничиваться некоторым определенным
значением всюду, где речь идет не о пути дерева, а о схеме дерева в целом.
----------------------------------
1. Вообразим в общих чертах рисунок
дерева. В воображении дерево будет представлено вершиной - узлом, в который не
входят никакие ветви и из которого выходит множество ветвей, каждая из которых
входит в узел, для которого она является единственной входящей ветвью. В свою
очередь, из каждого из множества узлов выходит множество ветвей и т.д., пока не
дойдем до конечных узлов. Мы можем в таблице выделить уровни дерева, начиная с
вершины, которую обозначим в качестве первого уровня, затем выделяем второй
уровень, представленный множеством узлов, в которые входят ветви первого уровня,
и т.д. Все узлы одного уровня мы можем упорядочить, проиндексировав их т.о.,
чтобы рядом находились узлы, имеющие общий узел верхнего уровня. В свою очередь,
все последующие уровни упорядочиваются на основе порядка предшествующих уровней.
Тогда данные уровней могут быть записаны в таком порядке:
1 уровень: 1.
2
уровень: 1.1, 1.2, 1.3,...
3 уровень: 1.1.1, 1.1.2, ...., 1.2.1,
1.2.2,...,1.3.1, 1 .3.2, ....
4 уровень: 1.1.1.1, 1.1.1.2,...
Т.о. в n-ом уровне оказывается записана вся информация о структуре дерева,
если все пути дерева имеют одинаковую длину, где под длиной пути понимается
число уровней, которым принадлежат узлы пути. В общем случае, однако, длина
путей дерева может быть различна. В этом случае дерево должно быть записано в
соответствии данными его конечных узлов. например, 1.1.1, 1.1.2,...,
1.2.1,1.2.2, 1.2.3, ... 1.3.
2. Это пример случая, когда вначале строится
представление, описывающее некоторую часть чувственной реальности. Благодаря
представлению возникает знание и, как следствие, понимание и, соответственно,
понятие того, что представляет собой объект, выделенный из данных чувственной
реальности. Создание представления, описывающего чувственную реальность и
представляющего собой результат
конструктивной деятельности,, содержит в себе в неявном виде чувственную
реальность, с одной стороны, и её понимание - с другой. Следует дополнить
сказанное тем, что в настоящем случае речь идет об абстракции дерева, созданной
человеком на основе чувственных данных - ветвлений реальных деревьев. В этом
смысле человек наряду с чувственной реальностью создает реальность представлений
об этой реальности - и когда эти представления обозначаются словом, то слова
начинают жить самостоятельной жизнью, которая
предполагает, а не полагает представления как объекты жизни мышления,
которое говорит
не о положенном, а о предположенном, и которое посредством представлений
отделено от непосредственно данной чувственной реальности, принадлежа
к духовной сфере жизни человека, но абстрактная форма
которой может быть представлена человеком в чувственном виде в форме слов и
знаков как созданий человеческого интеллекта. Необходимость перевода
представлений в чувственную форму слов и знаков диктуется тем, что
чувственная форма представления объектов интеллекта является единственным
способом передачи интеллектуальной информации.
3.. Пути, которые проходит автор и читатель, противоположны: автор
должен представить понятия посредством представлений, выраженных в чувственных
формах. Читатель должен проделать противоположный путь, идя от чувственно
представленной интеллектуальной информации
в её духовной форме к предполагаемым ею
образам чувственной реальности. Автор вполне может заняться
самопроверкой, ставя себя на место читателя и занимаясь построением
чувственных образов на основе представляющих их систем знаков.
Матричное представление
Запишем множество уровней в виде вектора-
столбца, а каждому значению столбца поставим в соответствие -
соответствующую вектор-строку. Столбцу ставится в соответствие множество
строк. Затем, каждая из строк, в свою очередь, преобразуется в столбец, и ей
ставится в соответствие множество строк. Это множество строк преобразуется в
столбец и ему ставится в соответствие множество строк и т.д. Это –
технология построения дерева.
Возьмём квадратную матрицу (рис.
1). Выделим в ней левый столбец и верхнюю строку. В ячейку, находящуюся на
пересечении столбца и строки, запишем единицу, которая обозначит вершину
дерева. В оставшуюся часть столбца запишем сверху вниз адреса узлов, которые
порождены вершиной. В строки справа от выделенного столбца запишем значения,
которые принимает каждый из узлов второго уровня..
Т.о., матрица
представляет дерево трёх уровней, где на пересечении столбца и строки
фиксируется уровень матрицы, которым рассматривается вершина дерева или узел
дерева, рассматриваемый в качестве вершины. В столбце матрицы записываются
адреса узлов, которые порождены вершиной, а в строках матрицы записываются
адреса узлов, порожденных узлами вершины.
Прежде, чем продолжить
построение дерева, условимся о терминах. Будем называть левую верхнюю ячейку
таблицы А-ячейкой. Ячейки справа от неё - B-ячейками, столбец под А-ячейкой
- А- столбцом. Строки справа от ячеек А-столбца - А-строками. Будем считать,
что у нас есть множество матричных таблиц, отвечающих указанным признакам.
Назовем их А-таблицами.
Итак, пусть у нас есть множество экземпляров
А-таблиц, одну из которых мы только что заполнили. Примем следующее правило
построения дерева посредством таблиц. Если есть некоторая заполненная
А-таблица, то для перехода к следующим А-таблицам мы осуществляем следующие
действия:
1. Размножим заполненную А-таблицу числом копий, равным
числу заполненных ячеек А-столбца.
2. Перемещаем
содержимое А-ячейки в непосредственно примыкающую к ней справа В-ячейку и,
соответственно, содержимое В-ячеек, если оно есть, вправо.
3. Берем заполненный А-столбец и последовательно вносим его значения в
А-ячейки копий А-таблиц.
А-строки,
соответствующие заполненным ячейкам А-столбца, записываем в А-столбцы.
4 Ставим в соответствие ячейкам А-столбцов строки, записывая в них
адреса узлов, в которые преобразуются узлы ячеек столбцов
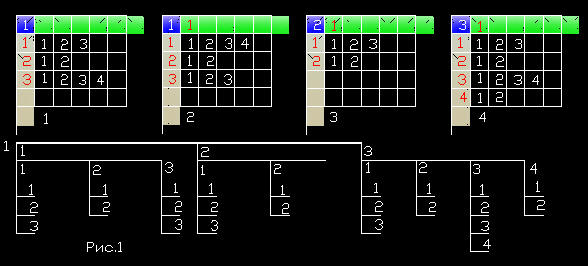 Пример построения (рис. 1) Берем
таблицу 1, записываем в А-ячейку узел вершины дерева -единицу, и в А-столбец
множество узлов, который она порождает. Каждая цифра представляет адрес (или
имя) узла. Каждый узел, в свою очередь, порождает своё множество узлов,
адреса которых записываем в соответствующие строки. У нас три узла в
А-столбце, поэтому берем три копии таблиц. В них перемещаем содержимое
А-ячейки вправо, а в оставшиеся свободными А-ячейки заносим адреса столбцов
таблицы 1. В результате получаем три А-таблицы, в А-ячейках которых стоят
различные адреса А-столбца таблицы 1. Вносим в столбцы 2-4 таблиц
соответствующие А-строки таблицы 1 и задаем значения переходов для
каждого из значений столбцов. В результате получили дерево рис.1, ветвление
которого можем продолжить в соответствии с заданным алгоритмом. При этом
произойдёт очередное смещение данных А-ячейки и в В-ячейках, причем, в
качестве исходных у нас будут теперь выступать все три А-таблицы: 2,3,4,
причем, все они в А и В ячейках будут содержать указатели на информацию обо
всей предшествующей истории формирования дерева.
Общепринятый
способ записи дерева в технической и научной литературе в качестве
оглавления.
1(1(1(1(1(12)2(123)3(1234)4(12))...
1а(1б(1в(1г(1с(1д(1е(12)2е(123)3е(1234)4е(12)) 2д((1е(1234)2е(12))3д(1е)...
Представление дерева структурой многоразрядных чисел
Ради удобства сделаем такое ограничение, что число порождаемых узлом
нижележащих узлов не может быть больше десяти, причем, ноль будет обозначать
10 и идти после 9. Тогда, если мы возьмём произвольное многоразрядное
десятичное число, например, 3525, то с каждым разрядом соотносим узел,
и т.о. число узлов, представляемых числом, равно числу разрядов, и адрес
каждого узла равен номеру разряда при подсчете разрядов числа слева направо.
Число разрядов числа представляет множество узлов, порожденных
соответствующим им вышестоящим узлом, который также, в свою очередь,
принадлежит разряду вышестоящего числа. В свою очередь, цифры каждого из
разрядов числа обозначают количество порожденных узлом, представленных
разрядами. Т.о., в числе 3525 первый узел порождает 3, второй – 5 и т.д.
нижележащих узлов. Если мы имеем три числа 3256, 43546, 127827,
расположенных в данном порядке, то они порождены числом 456, так как первое
число имеет 4, второе-5, третье – 6 разрядов, которое, в свою очередь,
порождено числом три. Т.о. дерево трёх уровней будем выглядеть как 3→456→3256,43546,127827.
1. Любой конечный узел
дерева может рассматриваться в качестве вершины, от которой дерево строится
дальше.
2. (Идея отождествления субъекта с точкой дерева)
Принцип адресации определяется тем, в какой точке дерева мы находимся. Та
точка дерева, в которой мы находимся, рассматривается в качестве вершины
того дерева, которое она порождает и адресация в этом случае может идти не
от начальной вершины дерева, а от точки, в которой мы находимся. Из этой
точки мы можем видеть только порожденное ею дерево и своего родителя.
3. Такая вершина дерева может называться субвершиной, и в качестве
субвершины может браться любая точка дерева. При этом будем считать, что
любое такое выделение связано с отождествлением субъекта с этой точкой.
4. Листья дерева отличаются от узла тем, что принадлежат чувственной
сфере, в отличие от узлов, которые принадлежат понятийной области. На
практике дерево совершенно не обязательно заканчивается листьями.
5. Возможно противоположное движение – от чувственности – к абстракциям,
от листьев ко всё более общим понятиям.
|
