на главную страницу

    L51

L51_4 Конспекты

   L51_4.2 Предел
    Переход к интегралу
    Составление уравнений

L51_4.1

    

   

    Изложенная идея n-мерного пространства и также интервалов просты. Также простыми являются операции с интервалами в n-мерном пространстве. Меня же заинтересовало следующее обстоятельство, касающееся функции. Что такое функция? Это какое-то соответствие в n-мерном пространства. Пусть у=2х. Что такое в этом смысле функция? Это не что иное, как способ указания на соответствие  между значениями, скажем, двух прямых.
    Мы говорим: х= такой-то величине, у - такой-то величине. Сама по себе функция выражает некоторый общий закон, который связывает числовые значения переменных, и таких законов, связывающих их, может быть сколь угодно много.  С другой стороны, мы говорит, что х принимает такое-то значение. Но при этом мы должны различать две вещи: Что такое значение х на прямой - это определенная точка прямой. Однако на прямой существует множество точек, и эти точки мы должны иметь возможность различать друг от друга, а для этого нужно иметь адрес этой точки, а адрес этой точки представляется интервалом, определяемым от начальной нулевой точки отсчета. Но произвольный интервал  представляет собой упорядоченное множество точек, адрес каждой из которых определяется относительно некоторой начальной точки отсчете. Т.о. мы получаем понятия абсолютной и относительной точек отсчета. Всё, что ни делается, любая теория - делаются ради приложений, которые ими обеспечиваются. Если выбрана абсолютная система отсчета, относительно которой определяются нулевые точки n-мерного пространства, то относительные системы координат характеризуются тем, что в качестве нулевой точки отсчета берется, скажем, нижняя граница интервала. Во всяком случае, всю совокупность чисел можно рассматривать в качестве универсального интервала. О чем я хочу сказать. Пусть две интервала х=(0,10) и х=(0,5). Сокращенно можно то же самое записать как х1=10, х2=5, имея ввиду, что начальная точка обоих интервалов равна 0. Тогда разность 10 - 5 = 5. Так мы обычно пишем. Но ведь в реальности мы имеем нечто другое: х1-х2=(0,10)-(0,5)= (6,10) Т.о., здесь важна не только числовая величина интервала, но и расположение интервала на числовой оси. Пусть х2-х1=(0,5)-(0,10)=(-5,0), ибо здесь уже поменялся вектор счета: он из положительного превратился в отрицательный, другими словами, изменилось на противоположное направление счета. Представим себе, что мы осуществляем подсчет от минус к плюс бесконечности. Мы получим ось, которая лишена противоположности, и само по себе понятие ноля представляется излишним. В реальности, однако, нами выделяется нулевая точка. И это связано с тем, что нами решаются какие-то практические задачи,  и наши действия приводят к положительным либо отрицательным результатам относительно точки, с которой нами начато движение.

      100612
    Слова служат для управления образами. Они вызывают образы. Или, напротив, удаляют образы, делают их невозможными.
    21. Идея измерения. Мы измеряем что-то чем-то, например, расстояние временем. Одно дело, когда расстояние измеряется расстоянием же. И другое дело, когда какие-то категории, например, расстояние, измеряются чем-то другим. Отсюда мы получаем, что в качестве инструмента измерения может использоваться функция. Но самой по себе функции, которой определяется однозначное соответствие между двумя величинами, недостаточно. Ибо измеряться должна не точка. Точка не имеет измерения. Измеряться должны интервалы.
    22. А что такое измерение интервалов? Это как раз и есть дифференцирование и интегрирование. При этом функцию следует рассматривать в качестве явления сущности. Или, другими словами, значением функции измеряется значение аргумента. Если функция рассматривается в качестве явления, то за этим явлением мы должны видеть сущность. Но что это означает? Это означает, что должна быть известна обратная функция. Что это означает далее? Что прямая функция может рассматриваться в качестве функции природной, которая проявляет какую-то сущность. Обратная функция позволяет измерять эту природную функцию через её явление. Например, если дана природная функция у=2х, то обратная функция будет х=у/2.
    23. Но нас не могут интересовать значения точек. И именно потому, что чтобы осуществить измерение чего-то через что-то, нужно иметь по крайней мере две точки, которые сравниваются друг с другом, такие, что одна из точек выступает в качестве критерия сравнения а вторая точка рассматривается в качестве того, что сравнивается с этим критерием. Всё дело в том, что если мы существуем постоянно в одной точке, то мы постоянно и находимся в ней и поэтому мы оказываемся влекомы этой точкой: для на не существует времени и не существует изменения именно потому, что для нас некоторая точка всегда равна самой себе.
    24. Итак, нам нужно иметь две точки: начальную точки, или точку отсчета, или точку, которая выступает в качестве критерия для сравнения, и конечную точку. И то, что мы определяем, это приращение, то есть изменение, связанное с различием между конечной и начальной точками. Сама эта идея измерения представляет собою способ рационализации, удвоения мира или объективация человека по отношению к самому себе, связанная со временем, когда человек осознает изменение каких-то параметров в связи со временем.
    25. Итак, нас интересует не значение точки или множества точек, взятых самих по себе, а значение одних точек, взятых по отношению к другим. Тогда, например, пусть мы имеем значение начальной точки, равной 4, конечной - 8. Тогда разность между этими двумя точками будет равна 4. Тогда, на основании этих данных мы можем определить значения точек аргумента прямой функции. Для точки 4 получаем значение аргумента 3, для точки 8 - значение аргумента 4. Т.о., посредством знания интервала у мы измерили значение аргумента х.
    26. Значение измерений сугубо практическое. Дело в том, что явление - это следствие. Это уже то, что произошло. И на следствие как на то, что уже произошло, мы неспособны влиять. Для того, чтобы изменить следствие, нам нужно изменить причину, чтобы изменить явление, нужно изменить сущность. Мы должны воздействовать на сущность.
    27. Это - одна сторона дела. Другая сторона дела относится к предвидению того, что будет дальше. Для того, чтобы обеспечить предвидение, нам недостаточно иметь дело с двумя точками, то необходимо иметь дело по крайней мере на каждом шаге исследования с тремя точками для того, чтобы получить возможность определить закономерность изменения явления. В связи с этим, возникает вопрос о последовательности шагов измерения, которые, очевидно, должны быть одинаковыми: каждый из шагов должен быть равен любому другому шагу. А если все шаги одинаковы, то можно говорить о тех или иных значениях каждого шага как о сомножителе, так как все эти численные значения все будут одинаковы.
    28. Если мы имеем две точки, то они должны быть связаны прямой линией как кратчайшим отрезком между точками. Если теперь полученный нами отрезок разделим на множество одинаковых отрезков и определим значения конечных точек каждого из них, то мы можем определить соответствующие точки, значения их, и затем, соединив их все, мы получим значения флуктуаций относительно прямой, которые могут быть как случайными, так и подчиняться некоторой определенной закономерности.

   
    Добавление 1. Когда мы явно задаем какое-то число, то неявно предполагаем не эту единственную точку, но эту точку по отношению к нолю. Следовательно, в действительности мы рассматриваем интервал. С другой стороны, та же самая точка из множества точек может быть выделена лишь постольку, поскольку задан её адрес.

    Добавление 2.
   100612
    1. Ты говоришь: представлять. А что ты можешь представлять, кроме образов. Или схемы образов. Нужно также еще соотносить слова и образы. Для того, чтобы что-то воспроизводить, нужно иметь точку отсчета, по отношению к которой осуществляется воспроизводство. Возможно, в качестве точки отсчета может быть что угодно. Например, для того, чтобы воспроизвести текст об измерениях, можно взять эпизод, когда Анна Каренина едет на вокзал. Для психологического воспроизводства воспринятого материала также необходимы две точки: точка, по отношению к которой рассматривается воспроизводимое, и воспроизводимая точка.
    2. Можно говорить о непосредственных и опосредованных измерениях. Непосредственные измерения - это измерения явления по посредством присущих ему единиц измерения. Например, измерение расстояния посредством сантиметров, метров и т.п. Опосредованные измерения - это измерения чего-то в единицах чего-то другого. Например, измерение расстояний посредством времени. Для этого нужно обладать знанием функции, которой связываются перемещение в пространстве и время перемещения. Опосредованное перемещение уже предполагает движение, процесс в отличие от непосредственных измерений, в которых мы имеем дело с множеством рядоположенных, не связанных друг с другом точек.
    3. Опосредованное измерение устанавливает соответствие между явлением и сущностью и посредством видимого явления измеряется невидимая на этом этапе сущность. С другой стороны, всякое наше действие порождает те или иные следствия, выступая в качестве их причины. Причина по отношению к следствию выступает в качестве сущности следствия. Наши действия, т.о., выступают в качестве сущности по отношению к следствиям, которые в этом случае являются следствием сущности. Однако понятия причины и следствия являются более узкими, частными относительно соотношения сущности и множество форм её явлений в зависимости от её контекстов.
     4. Итак, осуществляя определение сущности через явление, мы определяем состояние сущности, вызвавшей данное явление.
    5. Движущаяся сама по себе точка не предполагает памяти, и поэтому все происходящие изменения с человеком человеком не замечаются, поскольку он всегда находится в той точке, в которой он находится в данный момент и тем самым человек оказывается тождественен с этой точкой. Память необходимо связана со сферой идеального, отрывом от непосредственно данной чувственной достоверности, переходом человека из состояния тождественности его с производящими его обстоятельствами существования в состояние идеального, оторванного от чувственной достоверности и тем самым к противопоставлению чувственно достоверности в силу того, что точкой отсчета для него становится идеальное.
    6. Возникновение памяти возможно только лишь на основе сравнения предыдущего и последующего, то есть на основе фиксации изменения между точками, преобразования непрерывно текущей чувственной достоверности в достоверность дискретную, в фиксацию непрерывно изменяющейся реальности во множество отстоящих друг от друга на определенную величину шагов мгновенных снимков с реальности, и категория движения здесь возникает на основе введения категории времени относительно снимков. Метафизический подход не доходит до этого и рассматривает эти отдельные снимки преобразующейся, изменяющейся сущности как разные, отдельные объекты, никак не связанные между собой. Однако анализ общего, которым характеризуются различные снимки, приводит к пониманию лежащей на ними общей сущности, что заставляет рассматривать эти различные объекты как виды одной и той же идеи. Т.о., мы получаем разветвление на диалектику, которой исследуется движение объектов, и метафизики, которой исследуются объекты движения и производится их классификация относительно друг друга.
L51_4/1 Измерения выход

L51_4.2 Предел

  |= Величина. Изменение численного значения величины. Переменной называется величина, принимающая различные численные значения. Если численные значения величины не меняются, то она называется постоянной. Постоянная величина может рассматриваться в качестве частного случая переменной, у которой все численные значения одинаковы.
    Промежуток, интервал a<x<b - отрезок, сегмент a≤x≤и  замкнутый интервал или промежуток (a,b), [a,b], [a,b) полузамкнутый промежуток
    Окрестность точки - произвольный интервал, содержащий эту точки внутри себя.  если точка находится в центре интервала, то она называется центом окрестности. . Величина (b-a)/2 называется радиусом окрестности.
    |=
    Относительность постоянной и переменной величин: все зависит от контекста, в котором величина применяется, или, что то же,  от принятого масштаба измерения.
    Когда говорят о числах, то отвлекаются от того обстоятельства, что каждое число представляет собой какой-то масштаб изменения. Например если мы берем десятичные числа, то мы имеем с классом совместимых единиц измерения. Однако, если мы возьмём четные и нечетные числа, то мы сразу же наталкиваемся на несоизмеримость соответствующих единиц и поэтому, соответственно, мы должны говорить о качественной противоположности этих чисел. Тогда как если говорят об иррациональных числах, то здесь видится вещь, связанная с операциями умножения и деления. Но умножение и деление - это частный случай сложения, и поэтому также и иррациональные числа должны быть сведены на операции сложения и вычитания. Затем, отношение между противоположностями характеризуется тем, что оно характеризуется определенным вектором. То есть противоположности не симметричны друг другу, иначе всегда был бы круг и невозможна была бы спираль. Соответственно, и операции сложения и вычитания не являются симметричными операциями, и это же, как следствие, относится и к умножению и делению. Невозможно нечто вычесть из ничего. Чтобы нечто вычесть, нужно иметь то, что вычитается. Поэтому если из ничего вычесть что угодно, то так ничего и останется. Вычитание - в физическом мире это определенное действие. Если есть 5 руб, то из них можно вычесть 5 рублей, и не более того. Что вообще представляет собой вычитание с точки зрения категории бытия. Операция вычитания есть перемещение. Если мы имеем множество А с n элементами, то из множества А мы можем взять  m,<n. Но те элементы, которые нами вычтены из множества А, появились в некотором множестве В, в силу чего произошло прибавление элементов во множество В. С физической точки зрения невозможно вычесть что-то из чего-то без того, чтобы вычтенное не было прибавлено к чему-то другому. Но если так рассуждать, то точно также невозможно и прибавить что-то к чему- без того, чтобы оно не было вычтено из чего-то. Всякое прибавление чего-то к чему-то есть одновременно также и вычитание этой величины откуда то. Ничто не возникает из ничего и не уничтожается в ничто.  Разумеется, мы способны создать представление возникновения из ничего  или уничтожения в ничто  чего - то .  Но это будет всего лишь абстрагирование от одной из сторон действия.
    Нужно ходить по кругу. Написал кусок текста, затем возвращаемся к его началу и продолжаем его писать сначала.
    Так, мы говорили о несоизмеримости единиц, и связывали это обстоятельство с четными и нечетными числами, рассматривая их в качестве противоположных. Далее заметим вещь, относящуюся к множествам. Пусть множества А и В пересекаются, то есть имеют общие члены. На деле эти общие члены обладают различными свойствами и в множество вообще могут входить любые элементы, если они обладают свойством, которое представляет множество. Отсюда следует, что когда мы имеем дело с множествами, то мы имеем дело со свойствами. Категорией множеств представляются свойства. Объекты же, которые собираются в множество, сами по себе носят случайный характер, и сами по себе объекты всего лишь и имеют то общее с другими объектами, что это множество. Т.о., посредством категории множества отождествляются объекты относительно представляемого множеством свойства.  
    Поэтому в силу двойственности весь мир оказывается разделен на две противоположные части: то, что с одной стороны является вычитанием, с другой стороны является сложением.

   |= Упорядоченные переменные величины. х есть упорядоченная переменная величина, если известна область изменения этой переменной величины и про каждое из двух любых её значений можно сказать, какое значение предыдущее и какое последующее.
Определяя область изменения  переменной величины, это, например, целые числа 1, ... , 10. х=1,2, ... ,10/ (1,18)  { возрастающая или убывающая, если каждое её последующее значение больше или меньше предыдущего. Те и другие величины называются монотонными. Переменная величина называется ограниченной, если её значения принадлежать отрезку, но при этом не обязательно она принимает все значения из отрезка. 

    Предел функции.
    Предел функции непосредственно связан с принципом непрерывности.  Если есть какая-то точка а, к которой стремится х, и при этом существует точка b, которая стремится к у. (1,35). Для того, чтобы понять это определение предела, нужно осуществить обобщение на множество логических возможностей. Именно, стремление аргумента функции к какой-то точке сверху или снизу  может быть не связано со стремлением к какой-то точке функции, как и наоборот. Во всех этих вещах всегда присутствует чертовщинка, именно, функция может быть определена как можно близко к некоторому числу, но не определена в самом этом числе. Сам по себе этот принцип связан с десятичными дробями, бесконечно уменьшающими единицы измерения, но при этом все единицы измерения оказываются соизмеримыми, то есть укладывающимися целое число раз, именно в десять раз в старшем разряде единиц измерения.

   Предел переменной величины, предел функции.
    Предел переменной величины |x-a|<ε  Можно говорить  об изменении переменной величины. Но изменение переменной величины может осуществляться в двух противоположных направлениях, и что касается естественных процессом, то именно с этим мы и имеем дело. Затем, в естественных процессах  наблюдаемые изменения мы фиксируем пошагово. А шаг - это вещь счета, выражающаяся натуральным рядом чисел. Но в реальности мы всегда находимся на каком-то n-ом шаге, и счет мы можем относительно него осуществлять "вперед" и "назад" или "вправо" и "влево" При этом возможен переход шагов через ноль, и тогда также и шаги в отрицательной сфере должны фиксировать именно как отрицательные шаги. Соответственно, будет наблюдаться и переход и качественное изменение процессов с  отрицательных на положительные либо обратно. В свою очередь,  нужно иметь ввиду, что процесс происходит не только в данной точке, но и во времени и, кроме того, мы имеем дело со многими процессами, протекающими во времени, которые способны пересекаться по мере движения во времени в какой-то временной точке, давая какие-то качественно новые результаты, или же не пересекаться во времени и ни к чему не приводить. Поэтому у нас должна вводиться, наряду с категорией последовательности шагов, также и категория времени, которая, в отличие от шагов, характеризующихся по крайней мере двумя противоположными направлением, протекают во времени, которое имеет одно направление - из прошлого в будущее.

Переменная имеет предел, если её изменение стремится к какой-то величине, но не переходит через неё.
    Что такое переменная? Это - формула. Например, х_n=1*(1/n)
    Пусть х₁ =1/2,  х₂ =1-1/4, х₃ =1/8, х₄ =1-1/16, ...
    Здесь - переменная в контексте или закономерность переменной. Здесь две вещи: х и n, которое пробегает по натуральному ряду чисел; своего рода счет.
    М<x Движение . Здесь есть движение; и поэтому сами действия должны отражать движение (нужно знать и фиксировать, кто и что должен).  
    Итак, нам нужно выразить движение, а движение выражается только через сравнение; Движение непосредственно в языке не выражается; оно выражается через сравнение двух величин, и движение выражается разностью между ними.
    Сколько необходимо сравнений для выражения движения.
    Выражение линейного равномерного движения. оно характеризуется постоянным приращением и постоянным вектором. , например, 1/2, 1/4, 1/6. (Всюду нужно иметь ввиду, что мы имеем дело с интервалами, поэтому (0, 1/2), (0, 1/4), (0, 1/6). То есть отсчет идет от одной точки - "ноль". Напротив, интегрирование имеет дело уже с произвольными интервалами, имеющими начало в произвольной точке. ТО есть они отсчитываются от любой произвольной точки (натурального ряда чисел). Здесь - переход от абсолютной точки отсчета к относительным точкам отсчета; синтез того и другого достигается путем упорядоченного суммирования приращений.
    (0, 1/2), (0, 1/4), (0, 1/8), ... Здесь мы имеем шаги. С каждым шагом связано приращение; номер шага обозначается посредством n.
    Сравнение состоит в том, что мы имеем два шага - предшествующий и последующий. n-1 предшествующий шаг, - последующий. Разность функции между двумя разными шагами может быть одинаковой или различной
    Здесь - переход.: т.к. мы начинаем со сравнения двух величин, и на основе их сравнения устанавливаем отношение между ними в виде их разности или иначе. И задача состоит в том, чтобы связать значение переменной с номером шага. Т.о., должны быть привязаны значения переменной и номера шага; То есть значение переменной есть функция от номера шага. То есть если нам известен номер шага переменной, то по нему мы можем установить значение переменной; Но предпосылками для этого являются данные (имеется ввиду линейная закономерность) относительно двух соседних шагов. Но сравнения вообще представляют собой пирамиду. Если мы получили результаты сравнения шага 1, 2 и 2, 3, то мы можем сравнить полученные результаты между собой. Точно также, сравнивая результаты шагов 2, 3 и 3,4, мы также можем сравнить результаты сравнений, но также сравнить и результаты результатов сравнений и т.д.  Например, 1,2 =а, 2,3=б, а,б=с; 3,4=в; 4,5=г, в,г=д, с,д=е и т.д. В этом смысле мы получаем непрерывную ленту значений, а также и переходов.
    n=1)→то х=1/2; т=2, то х=1/4 Мы имеем дело с непрерывно разворачивающейся лентой и то, за закономерность чего мы можем отвечать, это за часть развернутой ленты. Например, вывод х_n=1/2ⁿ будет верен только для 1 и 2 шагов, тогда как если третий шаг даст 1/6, то верной будет формула 1/2n. Если же третий шаг даст 1/8, то верной будет первая из формул. Кстати говоря, здесь же мы получаем и общую схему построения формул. Но при этом мы, конечно, должны иметь дело именно с закономерностью. Для случая 1/6 мы имеем постоянную разность, для случая 1/8 - переменную, и мы имеем дело с нелинейной функцией.  Отсюда следует , что рассмотрение только двух точек недостаточно для определения, является ли функция линейной или нелинейной. Поэтому нужно взять по крайней мере 3 шага. Что дает каждый следующий шаг. Он дает переход к последующий точке Кстати, формула 1/2ⁿ характеризуется нелинейностью и степенью, причем, увеличение степени будет увеличивать крутизну кривой, однако при этом общая закономерность относительно направления кривой сохраняется. 

   Нахождение предела.
    Есть технология (нахождения предела), которой и нужно следовать. Эта технология должна быть описана (явно) .Итак:
    1. Задается число, которое рассматривается в качестве предела функции.
    2. Берется абсолютная величина разности функции и предела, которая должна быть меньше любого наперед заданного числа ε при условии, что разность аргумента

    Определение технологии.
    Если функция у=f(x)? то если х стремится к пределу а, то у?

   68. Переход не только к другой оси, но и к тому, что в другой оси может доминировать противоположный модус. Вообще оси рассматриваются как независимые друг от друга, хотя между ними и могут выполняться функциональные отношения.
   
    69. Переход к третьему квадранту даёт доминанту отрицательных положений. Но в силу того, что доминирует отрицательность, она представляет целое, и, представляя целое, она представляет счет. И поэтому не влияет на результирующий знак. И поэтому в результате мы должны получить минус. И поэтому люди, которые рассматривают процесс с положительной точки зрения, применяют к минусу отрицание, и т.о. минус выглядит как плюс. Дело в том, что сфера положительного и сфера отрицательного в положительной сфере на практике применяют только её; отрицательную не применяют и не способны применять. И, соответственно, и относительно отрицательной сферы то же самое.
    70. Переход в четвертый квадрант даёт в качестве аргумента положительное, в качестве функтора - отрицательное. Поэтому к положительному применяется с точки зрения положительного отрицательное и поэтому получаем минус.
    71. Переменная имеет область своего определения, т. е. она принимает значения по какому-то закону, Т.о. оказывается, что переменная и функция - это, собственно, одно и то же. Вопрос только в том, как, с какой стороны они рассматриваются.  

   78. Весь вопрос заключается в том, как непрерывность выражается через дискретность. Нужно, чтобы непрерывность в дискретности предполагалась, существовала в снятом виде.  

Показательная и логарифмическая функции

    

    Пусть дано выражение 1.1/2 (=1(1/2) это - не произведение, это - величина числа, потому что 1*.1/2=1/2. Умножить на 1/2 - это всё равно, что единицу разделить на два. На самом деле выражение вида 1.1/2 означает не умножение, а сложение, именно, 1+.1/2=1.1\2. Поэтому пределом выражения вида 1.1/n является единица, т.к. 1/n стремится к нолю. (1.33) Доказательство: x_n-1 (то есть вычитаем из числа предел, к которому он стремится)=|(1+.1/n)-1|=1/n. Здесь важен непосредственный переход от смешанной дроби, если под ней понимать целую и дробную часть числа, к сумме целой и дробной частям числа. Тогда, задав любое число ε, например, равное 0, 1, начиная с номера n, большем 1/ε? даст разность |x_n-1 |<ε  Так, если ε=0,1, то n>1/.0,1=10. Тогда n=1 будет меньше ε.

    x_n=1+(-1)ⁿ(1/2ⁿ)  Выражение (-1)ⁿ определяет знак минус для нечетных чисел и знак плюс - для четных.  Дробь 1.1/2 =1+1/2? то есть целая и дробная части дроби равны их сумме. Величина стремится к пределу, колеблясь вокруг него. Вначале высказывается идея о том, что являетя пределом числа;Затем эта идея проверяется. Если пределом является 1, то |x_n - 1|=|1+(-1)ⁿ(1/2ⁿ)-1|=1/2ⁿ
    1/2ⁿ < ε  откуда 2ⁿ > 1/εТсоотвествие: А = log_aN -- a^A = N. nlg2 > lg.1/ε  Связь  показательной функции и логарифмической: вычисление произведения проще, чем степени, поэтому переход от показательной функции к логарифмической и обратно упрощает задачу. Говорят: логарифм по основанию "а". Что такое а? а - это число, возводимое в степень в показательной функции. Поэтому если мы переходим от показательной функции к логарифмической, то основание нам дано. С другой стороны, выражение вида log_a N = A. Здесь мы имеем дело с тремя переменными, и для определения одной из переменных нам нужно знать значения двух других.  1/ε, если ε - любое сколь угодно малое число, может давать любое, сколь угодно большое число. И это любое сколь угодно большое число есть n

    120612
    1. Логарифм и степень. Логарифм есть операция, противоположная возведению в степень. То есть логарифм - это извлечение корня. Произведение вычисляется проще, чем показатель степени. Как осуществляются операции логарифма и показательной функции. Они представляют собой по отношению друг к другу противоположные операции, и, следовательно, если в одном случае мы имеем дело с показателем степени, то в другом случае мы должны будем иметь дело с извлечением корня.
    2. Над той или иной новой операцией работает весь мозг, а не какая-то его отдельная часть.
    3.  2 в кубе равно 8. Но корень в третьей степени из 8 равен 2. Т.о., под словом "логарифм" понимается показатель корня. То есть это - обратная операция. Поэтому, когда мы говорим о логарифме числа N по основанию а, то мы имеем ввиду корень (степень корня), применение которого к N даёт основание а логарифма.
    4. Если задано какое-то число, то - множество оснований в качестве сомножителя в нём. Если дано число, то мы можем извлекать из него различные корни, и при этом будем получать только лишь приблизительные результаты по большей части. И это сравнительно с возведением в степень, которое дает всегда точный результат. Всякой прямой операции - в данном случае возведению в степень - соответствует обратная операция. Но как только мы начинаем в качестве прямой операции рассматривать обратные операции, мы приходим к несоизмеримости в общем случае применяемых единиц.

    Законы логарифма:  log (N1*N2) = log N1 + log N2  логарифм произведения двух чисел равен сумме логарифмов эти- чисел, а логарифм частного от деления двух чисел равен разности их логарифмов.
    Логарифм числа в степени равен произведению степени на логарифм этого числа, а логарифм корня из числа равен частному от логарифма этого числа и его корня.
    Логарифм числа по основанию а равен частному
   

     [1]]  Пискунов. Дифференциальное и интегральное исчисления.|=

L51_4.3 Измерения

    100612
    Слова служат для управления образами. Они вызывают образы. Или, напротив, удаляют образы, делают их невозможными.
    21. Идея измерения. Мы измеряем что-то чем-то, например, расстояние временем. Одно дело, когда расстояние измеряется расстоянием же. И другое дело, когда какие-то категории, например, расстояние, измеряются чем-то другим. Отсюда мы получаем, что в качестве инструмента измерения может использоваться функция. Но самой по себе функции, которой определяется однозначное соответствие между двумя величинами, недостаточно. Ибо измеряться должна не точка. Точка не имеет измерения. Измеряться должны интервалы.
    22. А что такое измерение интервалов? Это как раз и есть дифференцирование и интегрирование. При этом функцию следует рассматривать в качестве явления сущности. Или, другими словами, значением функции измеряется значение аргумента. Если функция рассматривается в качестве явления, то за этим явлением мы должны видеть сущность. Но что это означает? Это означает, что должна быть известна обратная функция. Что это означает далее? Что прямая функция может рассматриваться в качестве функции природной, которая проявляет какую-то сущность. Обратная функция позволяет измерять эту природную функцию через её явление. Например, если дана природная функция у=2х, то обратная функция будет х=у/2.
    23. Но нас не могут интересовать значения точек. И именно потому, что чтобы осуществить измерение чего-то через что-то, нужно иметь по крайней мере две точки, которые сравниваются друг с другом, такие, что одна из точек выступает в качестве критерия сравнения а вторая точка рассматривается в качестве того, что сравнивается с этим критерием. Всё дело в том, что если мы существуем постоянно в одной точке, то мы постоянно и находимся в ней и поэтому мы оказываемся влекомы этой точкой: для на не существует времени и не существует изменения именно потому, что для нас некоторая точка всегда равна самой себе.
    24. Итак, нам нужно иметь две точки: начальную точки, или точку отсчета, или точку, которая выступает в качестве критерия для сравнения, и конечную точку. И то, что мы определяем, это приращение, то есть изменение, связанное с различием между конечной и начальной точками. Сама эта идея измерения представляет собою способ рационализации, удвоения мира или объективация человека по отношению к самому себе, связанная со временем, когда человек осознает изменение каких-то параметров в связи со временем.
    25. Итак, нас интересует не значение точки или множества точек, взятых самих по себе, а значение одних точек, взятых по отношению к другим. Тогда, например, пусть мы имеем значение начальной точки, равной 4, конечной - 8. Тогда разность между этими двумя точками будет равна 4. Тогда, на основании этих данных мы можем определить значения точек аргумента прямой функции. Для точки 4 получаем значение аргумента 3, для точки 8 - значение аргумента 4. Т.о., посредством знания интервала у мы измерили значение аргумента х.
    26. Значение измерений сугубо практическое. Дело в том, что явление - это следствие. Это уже то, что произошло. И на следствие как на то, что уже произошло, мы неспособны влиять. Для того, чтобы изменить следствие, нам нужно изменить причину, чтобы изменить явление, нужно изменить сущность. Мы должны воздействовать на сущность.
    27. Это - одна сторона дела. Другая сторона дела относится к предвидению того, что будет дальше. Для того, чтобы обеспечить предвидение, нам недостаточно иметь дело с двумя точками, то необходимо иметь дело по крайней мере на каждом шаге исследования с тремя точками для того, чтобы получить возможность определить закономерность изменения явления. В связи с этим, возникает вопрос о последовательности шагов измерения, которые, очевидно, должны быть одинаковыми: каждый из шагов должен быть равен любому другому шагу. А если все шаги одинаковы, то можно говорить о тех или иных значениях каждого шага как о сомножителе, так как все эти численные значения все будут одинаковы.
    28. Если мы имеем две точки, то они должны быть связаны прямой линией как кратчайшим отрезком между точками. Если теперь полученный нами отрезок разделим на множество одинаковых отрезков и определим значения конечных точек каждого из них, то мы можем определить соответствующие точки, значения их, и затем, соединив их все, мы получим значения флуктуаций относительно прямой, которые могут быть как случайными, так и подчиняться некоторой определенной закономерности.

L51_4.4 показательная функция и логарифм

L51_4.5 Переход к интегралу

    47. Пусть дана декартова система координат на плоскости х,у. Каждая точка в этой системе координат представляется двумя числами. Но каждая из точек представляет собой два интервала, один (0,х), второй (0, у) В то же самое время точкой определяется площадь, определяемая этими двумя интервалами, то есть произведение ху. Из этого отношения мы переходим к интегральному исчислению. Теперь другая сторона дела. Определим площадь треугольника АВС. Пусть его вершина А совмещена с нулем системы координат. Как известно, площадь треугольника равна половине произведения основания на высоту. Возьмём для начала прямоугольный треугольник (рис. 1). Очевидно, что площадь треугольника равна половине площади, определяемой точками (0,0), (х,у) = А, В
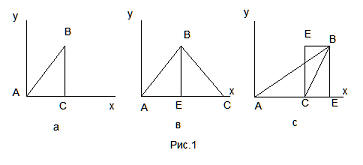Рис.1 в показывает, что площадь тр-ка АВС Далее все относительно площади треугольника понятно: все операции с исходным треугольником сводятся к построению на нём множества прямоугольных треугольников, посредством сложения и вычитания которых получается исходный.. Теперь возьмём функцию у=Ах + В. В результате мы получим смещение, площадь которого будет равна площади прямоугольника = х*у, и плюс площадь прямоугольного треугольника. В любом случае площадь полученной фигуры будет состоять из двух слагаемых: х*у + (х*Ах)/2 =Ах² . Отметим про себя, что если х и у связаны между собой линейной функцией, то мы получаем х₂ с коэффициентом. Аналогично это будет происходить  и со всяким хⁿ. Т.о., площадь, площадь площади и т.д. - в этом и оказывается тайна всевозможных квадратур, если переменные связаны между собой функционально. Исходная переменная появляется в значении функции, но уже в качестве квадратуры. Для любого фиксированного треугольника постоянная В может быть большой настолько, что площадь треугольника может не учитываться. Но, во всяком случае, С другой стороны, площадь любого прямоугольного треугольника равна половине площади построенного на его прилежащих к прямому углу сторонах . Т.о., мы получаем, что функция равна хв+Ах². 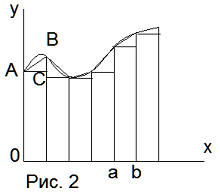Т.о., в любой функции мы можем выделить постоянную составляющую и переменную     Но мы имеем дело с интервалами. Поэтому если дан по оси х интервал (а,b), то он равен (0,b)-(0,a). Мы можем представить площадь фигуры, расположенной под линией функции у=f(x) как представляющую множество площадей соответствующих прямоугольников с соответствующими им треугольниками. Если интервал ∆х стремится к нолю, то мы можем кривую функции аппроксимировать соответствующими линейными функциями, причем, все они без исключения будут равны половине прямоугольника, занимаемого прямоугольным треугольником. И тогда вся площадь будет представляться как сумма, состоящая из некоторой постоянной величины  ху+Ах²... Например, у=х². Каждыое из приращений ∆х будет содержать некоторую постоянную величину, определенную предшествующим значеним фунции, и переменную величину, которая будет заключаться в интервале (х_i ,х_i+1 ). Другими словами, мы будем иметь  в качестве начальных постоянных значение площади   у_ix_i и половину произведения (у_i+1-у_i)(x_i+1-x_i)/2. И, т.о., фигуры будет равна ∑_i (у_ix_{i +} (у_i+1-у_i)(x_i+1-x_i)/2)

    48. Осознание.  (Все дело в том, что люди что-то делая, из чего-то исходят, но не осознают того, из чего именно они исходят. При этом они могут полагать, что исходят из чего-то совсем другого, но известного им. Тем самым задается противоречие между тем, из чего они исходят и тем, что они сами думают об этом. Это противоречие в конечном счете проявляется в получении результатов, отличающихся от ожидаемых, и тогда только начинает поиск. Но и в этом случае люди приходят к истинному результату, но при этом они действуют, не зная истинных причин. Осознание же приходит лишь после того, когда получат новый стереотип и тем самым возможность объективации своих действий, то есть рассмотрения их как объектов.)

L51_4.6 Составление уравнений

    46. Уравнения xyz = 863. Число уравнений должно быть равно числу переменных. Сумма последних двух чисел равна 9. второе число в два раза больше третьего. Мы получили два уравнения относительно двух переменных. Разность суммы двух последних чисел и первого числа равна 1. Получаем: у+z =9, y=2z, y+z-x=1 Закон ассоциации (x+y)-z = x+(y-z) = (x-z) + y Правило: разность суммы двух слагаемых и некоторого числа равна сумме разности одного из чисел и этого слагаемого и второго числа. Всё при построении уравнений строится на основе всевозможных опосредований. В связи с этим вопрос об употреблении опосредований

L51_4.7 Неравенства

    44. Принцип пропорциональности. 8>4 -> 2>1 Постоянное отношение сохраняется. В этом и состоит принцип пропорциональности. Мы делим обе части неравенства на одно и то же число, в результате чего отношение неравенства сохраняется. Отсюда мы получаем также общие законы оперирования с равенствами и неравенствами.
    45. В чем состоит цель: в том, чтобы имело место неравенство . Здесь движется одна точка: х, относительно постоянной бэта, при этом изменяется переменная у относительно постоянной эпсилон

L51_4.8   Плюс и минус

    47. Пусть дана декартова система координат на плоскости х,у. Каждая точка в этой системе координат представляется двумя числами. Но каждая из точек представляет собой два интервала, один (0,х), второй (0, у) В то же самое время точкой определяется площадь, определяемая этими двумя интервалами, то есть произведением ху. Из этого отношения мы переходим к интегральному исчислению. Теперь другая сторона дела. Определим площадь треугольника АВС. Пусть его вершина А совмещена с нулем системы координат. Как известно, площадь треугольника равна половине произведения основания на высоту. Возьмём для начала прямоугольный треугольник (рис. 1). Очевидно, что площадь треугольника равна половине площади, определяемой точками (0,0), (х,у) = А, В Относительно площадей рис. 1 в, с понятно. Но вот что мы можем сделать. прямая АВ есть линейная функция. у=Ах
    48. (Все дело в том, что люди что-то делая, из чего-то исходят, но не осознают того, из чего именно они исходят. При этом они могут полагать, что исходят из чего-то совсем другого, но известного им. Тем самым задается противоречие между тем, из чего они исходят и тем, что они сами думают об этом. Это противоречие в конечном счете проявляется в получении результатов, отличающихся от ожидаемых, и тогда только начинает поиск. Но и в этом случае люди приходят к истинному результату, но при этом они действуют, не зная истинных причин. Осознание же приходит лишь после того, когда получат новый стереотип и тем самым возможность объективации своих действий, то есть рассмотрения их как объектов.)
    49. Процесс приспособления не может исходить из двух неопределенностей. Всегда образец должен быть определенным и ясным. Тогда противоположная сторона должна будет доводиться до образца, приводиться в соответствие с ним.
    50. Эмоции вызывают только образы. Представления вызывают смесь эмоционального и двигательного эффектов, мышление же представляет собой только двигательный эффект, исключающий эмоциональный точно также, как эмоциональный эффект полностью исключает двигательный в той мере, в какой эти противоположные стороны осознанны. В этом случае противоположная сторона вытесняется из сознания и проявлять себя может только в инстинктивных действиях.
    51. Когда речь идет об умножении двух сомножителей, то один из них представляет собой одно из слагаемых суммы, состоящей из одинакового числа слагаемых, тогда как второй сомножитель указывает на число таких слагаемых. Особенность умножения при этом состоит в том, что каждый из сомножителей может выполнять как одну, так и другую функцию. Другими словами, если есть два сомножителя а и b, и функция слагаемого С, а функция числа слагаемых N, то можем записать С(а)*N(b)=C(b)*N(a). Теперь поставим вопрос об отрицательных числах и умножении положительных чисел и отрицательных Мысль состоит в том, что b не является ни положительным, ни отрицательным числом. То есть что следует различать понятия числа и понятия положительных и отрицательных чисел. как чисел, которые обладают смыслом лишь в условиях противопоставления их друг другу. Другими словами, имеет значение контекст, в котором употребляются числа. Пусть дана плоская прямоугольная система координат. Она содержит в себе четыре квадранта, отражающего соотношение двух осей координат. Так как площадь, определяемая каждой из точек системы координат, представляет собой произведение ху, то в соответствии с квадрантами мы имеем ху, х*-у, -х*-у, -ху. В связи с этим, возникает вопрос о знаке, который должна приобрести площадь. Тогда мы должны также поставить вопрос о разных функциях сомножителей в произведениях и тем самым также о разной роли осей координат. Например, если функцию b выполняет х, то у будет представлять величину слагаемого и указывать, сколько раз это слагаемое должно быть взято. Но если так, то не возникает вопроса, если b представляет собой число без знака. С психологической точки зрения число без знака - это объективация, рассмотрение объекта вне интересов, нахождение вне контекста, со знаком - включение в контекст, нахождение в сфере интересов. Если подойдем к вопросу с этой, то получим такую вещь, что из двух осей координат одна представляет числа без знака, и если это - ось абсцисс, то х в обе стороны от ноля принимает беззнаковые значения и является знаком числа слагаемых. Тогда знак произведения будет тот же, что и знак числа по оси ординат. Положение вещей изменяется, если мы исходим из противоположности чисел. и оставим принцип ведущей оси координат. Тогда, соответственно, мы будем иметь положительную позицию, и тогда вопрос, в чем она будет выражаться. В этом случае мы получим возможные определения полярности противоположной стороны и, соответственно, её количества, и это будет определяться только контекстом. Тогда получим, что если ++, то +, если +-, то -, если -+…. Но нужно иметь ввиду, что мы имеем две противоположные оси и, соответственно, два противоположных отношения. Поэтому возникает вопрос относительно того, являются ли равными отношения ху=ух? И другая сторона - содержательная. Итак, мы имеем точку отсчета, или доминирующую ось координат. Доминирующая ось координат себя рассматривает в качестве положительной или отрицательной. И тогда возникает вопрос: а возможно ли вообще умножение одной стороны на другую, и если возможно, то к.о. Ведь противоположности друг друга подавляют, а не усиливают. С другой стороны, мы имеем дело с инженерным подходом, и меня интересуют приложения математики, а не теоретическая математика. Тогда возникает вопрос относительно операции умножения знаков. И рассматривать эту операцию мы можем только с точки зрения сложения и вычитания, если рассматривать операции умножения и деления как сокращения для операций сложения и вычитания. Пусть дано отрицательное число -а, которое представляет собой множество n слагаемых, что сокращенно может быть записано как -аn=-(an) Например, если -а - долг, то -аn будет равно сумме долгов, и при этом происходит перенос отрицательного знака. Вообще следует говорить об относительности плюса и минуса. Этими знаками обозначаются противоположности. Нечто обозначается в качестве минуса лишь постольку, поскольку оно противопоставляется плюсу, как и обратно. Мы имеем, т.о., когда имеем дело с двумя координатами, с двумя объектами, которые противопоставляются друг другу или с одним объектом, в котором одни какие-то его части противопоставляются каким-то другим его частям. Особенность состоит в том, что в системе координат мы всегда находимся в одном из её квадрантов, и мы можем говорить о площади только данного квадранта, однако ведь мы можем начертить площадь , включающую в себя несколько квадрантов, в том числе и все квадранты. Но для этого мы должны будем иметь уже точки в соответствующих квадрантах. Но если так, то в этом случае можно также говорить о суммировании и вычитании площадей и, соответственно, о суммировании и вычитании точек (??) Суммирование и вычитание может вестись в одном и в разных квадрантах. Что касается одного квадранта, то тут всё представляется более или менее ясным. Но пусть у нас есть точки (а,b), (-a,b), (a,-b), (-a,-b). Им соответствуют площади в соответствующих квадрантах. Теперь представим себе, что мы сложили эти площади. Возникает вопрос, что в результате этого мы получим? И, основное, в чем будет заключаться смысл каждой из площадей? И что в этом случае будут представлять собой сложение и вычитание? Например, ab и -ab Если а - полученные деньги, и -а - деньги, которые я должен, то баланс будет равен нолю. И тут мы получаем новое понятие - баланса или равновесия противоположностей. Здесь а и -а выступают в качестве в качестве положительного или отрицательного определения объекта, а также числа раз, которое берется b. Тогда знаки должны быть связаны с операцией отрицания, и в том числе двойного отрицания, а также с операцией несимметричности, то есть вектора. Всё дело в том, что операция отрицания характеризуется тем, что отрицание, примененное к положительному числу, меняет его на отрицательное -(+а)=-а. Примененное к отрицательному числу дает положительное, то есть отрицает отрицательное. -(-а)=+а. В этом заключается тайна несимметричности, или вектора.
    52. Левым глазом при закрытом правом определять расстояния до объектов.
    53. Понятия отрицательной величины и отрицания связаны: они отождествляются между собой. Например, есть долг. Это - отрицательная величина. Отрицание долга, по логике вещей, должно давать ноль. Но если то же самое брать в количественном отношении, то если долг стоит 30 рублей, то есть характеризуется этой отрицательной величиной, то положительная величина, компенсирующая долг, будет +30 руб.
    54. Если применить симметричный принцип, то применение отрицания в положительном смысле к положительному, то есть двойное положительное, будет давать отрицание, а применение положительного к отрицанию будет давать положительное число.
    55. Когда мы имеем какую - то разность, то мы имеем одни и те же вещи. Во-первых, операцию отрицания как отрицание чего-то. В то же время применение к положительному объекту отрицания (вычитания). То же самое в суждениях: существует отрицание чего-то и утверждение чего-то. В том числе возможно утверждение отрицательного и отрицание положительного. В то же время существуют категории истины и лжи, такие, что истина - это утверждение того, что есть, и ложь - это отрицание того, что есть. Или утверждение того, чего нет.
    56 Пусть F₁ = F₂  (1). Тем самымF₁, F₂ отождествляются друг с другом. В то же самое время, в уравнении они противопоставляются друг другу, то есть относительно друг друга имеют противоположные знаки. Их противоположность не замечается именно потому, что они уже разведены по разные стороны. Противоположность проявится, как только мы их сведем в одну сторону:  F₁ - F₂ = 0  (2).. Здесь мы уже имеем дело с противоречием. Соответственно, мы имеем дело с двуия отношениями: одно дело, когда объекты друг другу противопоставляются и в этом противопоставлении отождествляются, и совсем другое дело, когда объекты, будучи перенесены на одну сторону, то есть действительно рассматриваются как объекты одного качества, вдруг обнаруживают отношение противоречия между собой. В формуле (1) объекты характеризуются одинаковыми знаками, в формуле (2) - различными. В формуле (1) оба объекта характеризуются положительными значениями, в формуле (2) положительным и отрицательным, причем, выражение, которое переносится на противоположную сторону уравнения, превращается из положительного в отрицательное. Т.о., положительность или отрицательность выражения зависит от его места в уравнении.
    Мы должны различать положительный или отрицательный модус объекта, и действия, операции с объектами. Поскольку речь идет об операциях над объектами, то здесь исходят из оператора отрицания, применение которого к объекту изменяет его модус на противоположные. В этой формулировке уже неявно содержит зпкон двойного отрицания: Применение к числк операции отрицания, к положительному - дает отрицательное число, к отрицательному - положительное: -(а)=-а, -(-а)=+а. Т.о. мы видим, что это - разные вещи - объект и действия с объектом. Объект характеризуется положительным либо отрицательным модусом. Действие над объектом характеризуется тем, что меняет его модус на противоположный. Однако в математике эти две совершенно разные стороны дела отождествляются и в силу этого обозначаются одним знаком. Если бы оператор отрицания обозначался каким-н. другим знаком, например, @ то ситуация выглядела бы иначе. Тогда @(+a)=-a, @(-a)=a. В этом случае не возникало бы путаницы между действием с объектом и модусом объекта. Но, видимо, принципиальная особенность математики как раз и состоит в абстрагировании от отличительных признаков вещей и на этой основе отождествлении в действительности не тождественного.
    Когда мы пытаемся содержательно интерпретировать операции на объектами с модусами объектов, то основная трудность возникает при интерпретации умножения друг на друга двух отрицательных чисел. Если бы мы делали различение между операцией над числом и числом как объектом, то мы получили бы такую вещь, что невозможно осуществить умножение двух объектов друг на друга вообще, это нонсенс. Умножение - это операция, это действие. И это - действие над объектами.  Значит, должны быть отдельно выделены объекты и действия с ними. Тогда каким образом у нас должно выглядеть умножение? 1. должны быть выделены объекты, с которыми производится действие. 2. должно быть определено действие. например, если 2*3=6, то мы получаем два варианта:  объект представляется числом два, тогда числом 3 определяется модус операции, именно то, что объект два должен быть взят три раза.  Либо же в качестве объекта берется число 3, и тогда действие умножения будет определяться модусом 2, показывающим, сколько раз мы должны взять объект 3. Математики от этих вещей абстрагируются, однако как только возникает вопрос о содержательном приложении математических абстракций, возникают проблемы. Так что приложении математических схем к реальности - это, в свою очередь, отдельная задача.
    Пусть теперь -2*-3. Как обычно, мы должны выделить объекты и операции над объектами. Допустим, в качестве объекта берется объект 2 с модусом -. Тогда *-3 будет выступать в качестве операции с её определениями. Каким образом применяется эта операция? 1. Выражение *-3 представляет собой сложную операцию, содержащую в себе операции умножения и операцию отрицания. Чтобы быть последовательными, мы должны были бы записать -*3. В этом случае сначала мы должны будем применить операцию отрицания к модусу числа 2, и затем осуществить умножение. Традиция математики, основанная на абстрагировании, иная, и пишут *-3., при этом имея ввиду -*3.  Но даже и в этом случае мы получаем правильный ответ, именно, -2*-3 = -(-2*3)=-(-6)=6. Т.о., получаем: -2*-3= -2 -*3. Однако постановка знака минус перед операцией умножения может создавать впечатление, что имеется ввиду вычитание. И тогда перед нами возникает дальнейший вопрос. Мы видим, что модус отрицания, операция отрицания и операция вычитания в математике обозначаются одним знаком, тогда как это - разные вещи. Однако против употребления формы -*3 выступает также еще и то обстоятельство, что операция умножения является симметричной, тогда как операция  вычитания таковой не является. Форма -2*-3 допускает также рассмотрение в качестве объекта -3,  и тогда справедливо к -3 сначала применить операцию вычитания, и к полученному результату - операцию умножения. Т.о., всё связано с тем, каким образом мы будем интерпретировать знак "-", в качестве знака модуса объекта или в качестве оператора отрицания. Т.о., если говорить о технологии перехода от абстрактных математических схем к содержательным схемам, то мы должны в первую очередь заняться ограничением абстракций, то есть ввести различение в отождествленное. Тогда весь процесс у нас выглядел бы т.о.: -2*-3 = -2*@3=@(-2*3)=6. Но тогда, для того, чтобы быть до конца последовательными, мы должны в первую очередь различать объекты и действия над ними. Математика именно тем и отличается от чувственной реальности, что реальность всегда конкретна, и то, что для математики является тождественным, для реальности является различным: мы можем расположить 2 шара в 3 ящиках соответствующего размера, или три шара в двух ящиках соответствующего размера. Для математики эти два расклада являются тождественными, но для чувственной реальности это различные вещи. Тогда переход от математических формул к содержательной реальности  должен быть связан с соответствующими обозначениями. Если о - объект, д - действие, то форма -2*-3=о-2д*-3, или же, так как мы будем иметь дело либо с объектом, либо с действием над ним, мы можем это записывать, указывая только объект либо действие, или, наконец,  в функциональном виде:  *-3(-2), где функтором *-3 обозначается действие или последовательность действий над объектом, а -2 выступает в качестве объекта, над которым производится действие. Тогда также и последовательность расположения операторов в функторе может соответствовать последовательности действий над объектом при условии, что либо действия операторов осуществляются слева направо либо справа налево в зависимости от удобства. Затем, речь должна идти об определениях. число 3 является определением умножения, но никак не отрицания. Но тогда мы должны ввести правило не только различения операторов и модусов объектов, но и их взаимного перехода одних в другие. И тогда мы должны сформулировать правила переходов, именно,  -(а)=-а и -а=-(а), где в скобках задается объект, вне скобок -оператор. Тем самым  как раз и берется определение связи оператора отрицания и модуса объекта, и поэтому мы должны записать:  -2*-3= -2*-(3)= -*3(-2). Независимо от того, в каком порядке мы будем применять операторы, мы получим один результат. -*3(-2)= - (*3(-2))=*3(-(-2)=6   
   

   78. Весь вопрос заключается в том, как непрерывность выражается через дискретность. Нужно, чтобы непрерывность в дискретности предполагалась, существовала в снятом виде. В этом смысле, слово является орудием, средством отражения непрерывности.  

L51_4.9

L51_4.10

L51_4.11

L51_4.12

L51_4.13

L51_4.14