Однако на первых порах сосредоточимся на технической и, соответственно, формальной стороне дела.
1. Мы можем вводить произвольные значения в произвольные ячейки. Особенность будет заключаться в том, что "в себе" или "сама по себе" ячейка имеет определенное значение или множество каких-то значений, относящихся к различным её сторонам. Однако мы этого не видим и не знаем. У нас всего лишь есть возможность задавать какие-то значения ячейке и получать реакции от неё. Эти реакции могут заключаться в том, что реакция будет непосредственной, то есть то, что было невидимым, проявится, либо опосредованной, путём проявления значений каких-то других ячеек, причем, здесь также может присутствовать опосредованность, когда заданное нами событие вызовет цепочку событий, таких, что одни части этой цепочки окажутся видимыми для нас, другие - останутся невидимыми, хотя и сработают.
В этом формальном подходе можно видеть содержательную сторону, если в качестве содержания рассматривать существующие зависимости между значениями ячеек, под которыми будем понимать их содержание.
Для реализации этой схемы сформируем дополнительно массив, представляющий матрицу, соответствующую таблице.
Для того, чтобы ввести принцип цели работы с таблицей, можно представить дело как игру, целью которой является перейти от ячейки (а,b к ячейке c,d) за минимальное число ходов или в соответствии с какими-то другими правилами.
Попробуем фантазировать. Некто вносит число в ячейку массива = некто вносит значение в массив - в предположении, что первоначально все значения ячеек равны нолю. Тогда порядок: 1. Внести значение в ячейку массива. 2. Значение - переход - два вопроса: либо переход в другую ячейку без изменения её содержания. Но возможно также, что значение ячейки при этом может быть изменено.
Во всём этом должно применяться правило: ничто не возникает и не исчезает. Просто одно переходит в другое. Поэтому если изменяется значение в одних ячейках, то соответственно должны происходить изменения в других.
Здесь могут быть две вещи. Со значением может быть связан переход. Со значением может быть связан выигрыш.
При этом такая вещь, что, изменяя значение, вы тем самым изменяете связи. Но тогда изменяется и характер связи, переходов.
Что такое переход? Можно предположить, что со значением ячейки связывается переход на другую ячейку. При этом здесь может действовать какая-то общая закономерность, принцип перехода, в частности, мы можем иметь дело с абсолютным переходом и относительным. Например, с числом 1 может быть связан переход на единицу вперед по строке и две единицы вниз по столбцу. В то же самое ячейка, которой принадлежит 1, имеет свои абсолютные значения в таблице, и поэтому также и для ячейки, соответствующей результату перехода, может быть вычислено её абсолютное значение.
Однако сами эти закономерности должны, в свою очередь, изменяться в зависимости от условий, например, в зависимости от сделанных перед этим ходов либо же под влиянием "грядущего".
Значит, такая вещь: мы задаем какое-то число и обращаемся к определенной ячейке. При этом может быть в результате внутренних операций изменен как номер ячейки, к которой сделано обращение, так и её значение, либо одно из двух.
Действия:
1. Можно иметь несколько массивов с разными структурами. Массивы в этом случае могут выступать в качестве вещей постоянных.
Вторая сторона этого же вопроса состоит в наложенных связях на массив. Как можно налагать эти связи: можно делать это таким образом, что если актуализируется одна ячейка, то будут актуализироваться и какие-то другие.
Другая сторона этого вопроса: если есть какие-то определенные данные, то в содержательном плане они могут играть роль условных или безусловных рефлексов, то есть представлять себя либо другое.
Цена хода.
Игрок начинает игру с какой-то принадлежащей ему суммой.
Каждый из ходов имеет свою цену. Для того, чтобы осуществить ход, игрок должен за него заплатить. Разные ходы могут иметь разную цену.
В результате хода человек либо выигрывает какую-то сумму, либо приближается к цели, либо не получает ни того, ни другого. Либо даже проигрывает.
Т.о., можно считать, что игрок платит за ход какую-то цену ради того, чтобы в результате хода получить выигрыш, пополнив тем самым свой капитал, либо реализовав какую-то иную цель.
Из всего сказанного выделить отдельные частные задачи и решать их.
Зависимости ячеек: если актуализируется одна ячейка, то актуализируются другие и деактуализируются третьи.
Актуализированные ячейки – это ячейки, с которыми можно действовать.
Что значит действовать? Это может означать, что значения ячеек будут изменяться в определенном направлении.
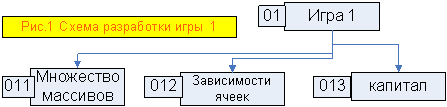
Теперь следует внести какой-то порядок в мысли, поскольку невозможно реализовать все сразу. Для этой цели вводится рис. 1, который в дальнейшем может конкретизироваться, обобщаться и пр. Теперь мы можем выделить отдельные темы и разрабатывать их независимо друг от друга. Здесь возникает вопрос с адресацией тем дерева. Просматриваются два варианта. Один вариант можно назвать позиционным: слева направо занимают начальная ветвь и, соответственно, узел дерева, затем следующий узел и т.д. В этой адресации явно не указывается номер узла сверху вниз (номер иерархии ветви) Второй способ адресации имеет ввиду полную информацию о ветви дерева. Такой адрес должен содержать в себе как номер иерархии, так и номер ветви в ней, и при этом должен указываться полный путь от начальной ветви до конечной.
01.11 Множество массивов.
Имеется ввиду, что следует иметь множество различных массивов, представляющих собой своеобразные карты содержаний игры с тем, чтобы в игре можно было заменять массивы и благодаря этому переходить в том числе и на разные уровни сложности игры. Но если так, то мы должны иметь банк массивов. В игре массив может называться картой. Значит, в программе должен быть раздел, относящийся к банку массивов, и в игре же должна иметь место загрузка той или иной карты.
На настоящем этапе разработки эти вещи должны оформляться в виде отдельных подпрограмм, которые мы пока вручную загружаем в основную программы.
Допустим, мы формируем банк. Так как здесь важен только принцип, пусть банк состоит из трех карт.
У нас не разработан вопрос о содержании самих карт, и поэтому карты у нас будут "пустыми" - загрузим пока массивы нолями. И у нас должна присутствовать операция по загрузке карты в программу.
Объявим массивы в качестве глобальных переменных (т.е. переменных, которые "видны" в любой подпрограмме)
Так как становится очевидно, что всевозможных подпрограмм может быть множество, то для соответствующих операций внедрения программ в программы нам может понадобиться множество событий, реализуемых, скажем, кнопками.
01.12 Карты
Инстинкту сложно работать с чистым формализмом. Формализм требует для себя какого-то содержания, какого-то смысла. В этом отношении при составлении карт удобно воспользоваться идеей маршрута. Можно представить себе, что мы имеем дело, например, с городскими автобусными маршрутами.
Карта может рассматриваться образца; это позволяет не смешивать задачу создания содержания с задачей его программирования.
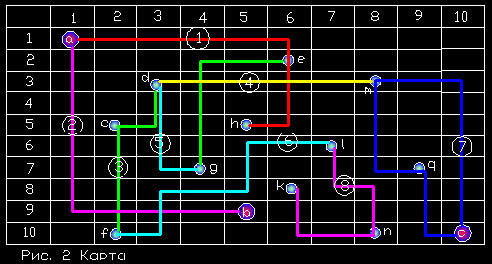
На рис. 2 представлен пример карты.
После того, как нам дана карта, на ней должно быть определено множество условных связей в соответствии с заданными маршрутами. Так, если "пассажир находится в точке (1,1), то у него есть выбор в качестве следствия попасть в точки (6,2), (5,5), (5,9). Если мы при этом вначале даём игроку сумму, скажем, в 10 единиц, и в то же самое время его поездка в разные точки имеет разную цену, которая вычитается из имеющейся у него суммы, то игроку нужно рассчитать свою поездку так, чтобы он потратил на поездку минимальную сумму. Усложнение игры может состоять в том, что, находясь "на какой-то станции", он видит только маршруты, которые связаны с нею. Дальнейшее усложнение игры может быть связано с "временем поездки".
Читатель помнит, что нашей целью не является построение игры ради игры. И он также помнит, что на каждой фазе разработки, на каждом шаге перехода к конкретике мы тем самым изменяем нашу собственную реальность, а изменение реальности позволяет формулировать новые идеи. И, как обычно, ради идеи мы бросаем реальность на половине дороги движения к ней, возможно, ради того, чтобы позже к ней вернуться. Так на какие идеи наталкивает нас новая реальность?
Недостаток игры состоит в том, что, если рассматривать её принцип с рефлекторной точки зрения, то и карта, и условия игры оказались подобны врожденным рефлексам, которые уже даны и в то же самое время находятся "по другую сторону нашей реальности". shSM в качестве познавательной способности занимается в этом смысле самопознанием. Если же подойти к вопросу со стороны условных рефлексов, то мы должны иметь возможность задавать их, то есть задавать, формировать связи. А когда эти связи заданы, они должны быть заложены в память. Это еще не есть весь условный рефлекс, но это - весьма значительная его часть. И тут возникает вопрос: как это можно сделать? Что касается задания связей, то тут не возникает особых проблем. Программа Table1 (программа Тable1 есть ранняя версия программы PTable1 и не приводится) позволяет задавать связи. Но на вопрос о том, как можно запомнить эти связи, ответа на этот вопрос у нас пока нет.
Как обычно, в программе Table1 есть два окна: для выбора программы и подпрограммы. В окно выбора программы занесите 1, выбора подпрограммы -2. В окна выбора условия (слева направо) выбираются номер столбца и строки таблицы и содержимое ячейки и далее условие выполнения, которое должно быть равно содержимому ячейки. В следующих окнах выбираете ячейку (столбец и строку) и содержимое как следствия. В этом случае у нас получается модель формирования условного рефлекса, когда совместно подаются условие и подкрепление. Существует общая форма, которая работает. Однако затем нам нужно иметь возможность подать условный раздражитель и получить результат. Как это сделать, остаётся под вопросом. Мы можем запрограммировать карту жестким образом, но с рефлекторной точки зрения это не представляет интереса, хотя на этой основе и можно было бы сделать интересную игру.