Отправляемся в поход. "И ты со мной"-ухмыляется Иван. - "А куда ж я без тебя"-отвечаю. Едем по городским окраинам. Обращаю внимание на недоумение Ивана, время от времени появляющееся на его лице.
Впереди показывается водная гладь, и на лице Ивана возникает оживление. Как рыбак, нарочно замедляющий вытаскивать пойманную рыбу, чтобы продлить удовольствие, Иван слезает с велосипеда и начинает разглагольствовать с местными пацанами. Удовлетворив потребность в разговоре, он сворачивает с дороги в проулок, где как раз упирается в выгребную яму и мужчину с ковшом на длинной деревянной ручке, с надвинутым на глаза длинным козырьком кепки, перемещающем содержимое выгребной ямы в огород. Иван смотрит на мужчину, мужчина разглядывает незнакомое лицо из-под козырька кепки. На немой вопрос Ивана мужчина усмехается: "Чтоб соседи не узнали". Иван поворачивает оглобли и возвращается на дорогу. "Хотел сократить"-говорит он мне. Для Ивана "сократить дорогу" - то же самое, что "нормальные герои всегда идут в обход". Только что двинулись, Иван: "Смотри, смотри, а я-то думаю, в чем дело, кручу педали, а сопротивления не чувствую, всё не мог понять, а, оказывается, цепи нет, цепь на переднем колесе, да смотри, и переднего колеса нет, я еду на заднем колесе, и как устойчиво. Вот замечательно!" Я молча смотрю на Ивана. "Да ладно, - заскучав, говорит он- только что-то не то, сопротивление действительно не то". - "У тебя цепь перескакивает на большую звездочку" - говорю я, взглянув на цепь. "А-а"-тянет Иван и, вместо того, чтобы наладить механизм переключения скоростей, чем бы я непременно занялся, успокоенный, продолжил часто крутить педали.
Выехали к воде. Вода оказалась каким-то озером. Иван начал раздеваться, но в это время в голове его что-то переключилось, и он переменил решение: "Едем обратно, скорее"- заторопился. "А что так?"- "Я тебе расскажу. На меня напала одна мысль. И ещё несколько лет назад. И я всё пытался её повернуть и так, и этак, а она ни с места. Я чувствовал, что за этой мыслью что-то есть, и, однако, почему-то никак не мог понять, что же в ней есть, и вот она не отвязывается от меня, сидит и зудит. Всё. Моё терпение лопнуло, разделаюсь с ней во что бы то ни стало"
Уже дома Иван продолжает: "Вот смотри, есть какая-то функция, какая угодно, для простоты пусть это будет у=0,5х. Как мы рассматриваем функцию. Фактически мы рассматриваем её последовательно, то есть задаем последовательно значения аргумента, и в результате получаем значения функции. Понимаешь, вот эта последовательность, в которой х как бы время, то есть х может быть чем угодно, но он разворачивается последовательно, есть эта непрерывная последовательность аргументов, и в результате мы получаем актуальное выражение функции как объекта, и мы представляем функцию графически, в данном случае это прямая с определенным наклоном по отношению к оси х. Моя мысль в чем: если есть функция, в общем, какая угодно, но определенная, а последовательность аргументов я задаю какую угодно другую во времени, то это будет уже нечто другое. Я хочу сказать, что мы можем иметь множество каких угодно функций как образцов, перерабатывающих аргументы функции в её значения. В реальном же времени мы задаем какие-то произвольные значения для последовательности аргументов функции, или иначе: есть последовательность аргументов функции - образца, из этой последовательности мы произвольно выбираем, "выдергиваем" значения, последовательно заполняя ими временную последовательность. Представим, для ясности, это графически (см. рис).
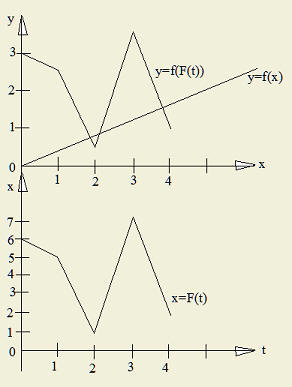Пусть есть функция у=0,5х. Будем придавать целым
единицам времени значения аргументов, которые, возможно, имеют в своём основании
какую-то нашу идею, так что выбор того или иного аргумента определяется
значениями множества функций образцов, перерабатывающих значения х в
значения у. В нашем примере это - единственная функция у=f(x). В
результате мы получим функцию х=F(t), которую
строим т.о., что сначала задаём точки:t 0 1 2 3 4
x 6 5 1 7 2
у 3 2,5 0,5 3,5 1
затем соединяем их прямыми и получаем непрерывную функцию х=F(t). После чего применяем полученные значения х в качестве аргументов для определения значений функции у=f(x)." - "И, т.о., получили сложную функцию у=f(F(t))." -заключил я. "Ну, да"-поскучнел Иван, но я с ним не согласился. "Тем самым тобой выявлен способ формирования сложных функций, который заключается в том, что значения внутренней функции являются аргументами внешней для неё. Что, конечно, не является ни для кого, кроме тебя, новостью, хотя для тебя это и немало. А что конкретно произошло, что сделала функция у=f(x) с функцией х=F(t) - она пропорционально уменьшила её значения в два раза. Обобщая, можем сказать, что функция у=ах, в зависимости от значений а уменьшает, если а меньше единицы, или увеличивает, если а больше единицы, значения функции у=F(x) в а раз. А отсюда, идя дальше, мы можем продолжить рассматривать содержательную сторону, беря в качестве образцов более сложные функции, и можем ставить дальнейшие содержательные вопросы, связанные с не пропорциональным умножением, делением. Фактически внешняя функция применяется к внутренней, так или иначе перерабатывая её". На этот раз не согласился со мной Иван: "Всё это не то." - "Что не то?" - "Не то, что у меня в чувстве". -"Что, опять этот проклятый материализм, опять не поймал за хвост чудо?" - съязвил я. "Да пошёл ты.- подосадовал Иван. - Скучный ты человек. И даже сам не представляешь, насколько ты скучен".
15.11.12 г.