По основному закону механики имеем: mwx =m(d2x/dt2)=R (1)
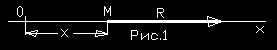Уравнение (1) называется дифференциальным (так как неизвестная х входит в уравнение под знаком производной) уравнением прямолинейного движения
. Оно также позволяет решать обратную задачу - по закону движения точки х=f(t) находить действующую силу F.Уравнение (1) может быть представлено в виде двух дифференциальных уравнений: m(dvx/dt) = R и dx/dt=dvx (7)
Если нужно искать зависимость скорости от координаты х, а не от времени t, то, т.к. dvx/dt = (dvx/dx)(dx/dt)= (dvx/dt)vx, получаем mvx(dvx/dx) = R (8)
Решение основной задачи динамики.
Так как сила R в общем случае может зависеть от времени t, положения точки х и от скорости vх=dx/dt, то уравнение (1) будет представлять собой уравнение 2-го порядка
d2/dt2 = R(t,x,dx/dt), общее решение которого имеет вид х=f(t,C1, C2), где С1, С2 - начальные условия. Чтобы решить задачу, нужно знать начальные условия, в качестве каковых выступают момент времени t, начиная с которого рассматривается движение, положение точки х в этом момент, а также её скорость dx/dt в этот момент.
В случае прямолинейного движения начальные условия задаются в виде: при t=0 x=x0, vх=v0, откуда х=f(t0, x0, y0)
На рис.1 представлен пример решения основной задачи на примере действия постоянной по модулю и направлению силы Q на точку.
Действие первое: формула, представляющая основной закон механики. 2. Обе части ур-ия умножаем на dt. В результате интегрирования получаем 3, из которого в четвёртом выражаем vx и в 5. определяем значение С1. Так как
vх=dx/dt, то 6; снова умножаем обе части ур-ия на dt, получаем 7, интегрируем
=8 и в 9 определяем С2.
В 10, подставив в 8 начальные значения, получаем закон движения точки.
Мы видим, что решение задач динамики включает в себя следующие этапы: 1. составление дифференциального уравнения. 2. Его интегрирование. 3. Определение постоянных интегрирования. 4. Нахождение искомых в задаче величин и исследование полученных результатов.
1. Составление ДУ.
а. Выбрать начало отсчёта, причем, если тело может находиться в положении равновесия, то начало отсчёта совмещается с ним.
Например, начало наблюдений за Александром (см. 026.11.1781) мы можем начать с просьбы к нему дядюшки поухаживать за Тафаевой. В этом случае должно быть определено состояние Александра на текущий момент. Его состояние должно быть смоделировано с точки зрения понятия равновесия, и для этого удобен образ, например, пружины. Пружина может находиться в трех состояниях. Определим состояние пружины как её внутреннее равновесие как ситуацию, когда она не растянута и не сжата. И, соответственно, два неравновесных состояния, когда пружина растянута либо сжата, при этом растянутая пружина стремится сжаться, а сжатая - растянуться. Воздействия внешней среды могут растягивать пружину или сжимать её. Если мы теперь представим себе субъекта как такую пружину, один конец которой жестко закреплен, а на другой конец воздействует внешняя среда, и если считать нормальным состоянием субъекта такое состояние "сжатия или разжатия его пружины", то есть такого рода давление на него (на его тело, физиологию) внешней среды, которое психологически воспринимается им как нормальное для него. Вообще заметим здесь, что под равновесием субъекта будем понимать форму равновесия между его физиологией и психологией, между потребностями его тела и его психики (души, духа, если хотите). В этом случае чувство равновесия может рассматриваться как своеобразная граница между внутренним и внешним мирами субъекта. Тогда сжатие пружины будет означать напряжение во внутреннем мире субъекта, разжатие - напряжения, которые связаны с его внешним миром. При этом перемещение фактической границы во внутреннюю либо внешнюю среду относительно номинальной границы субъекта неразрывно связано с соотношением сил субъекта и внешних давлений на него. Предыстория Александра до встречи с Тафаевой заключалась в том, что Александр со своими юношескими понятиями пытался войти в "мир взрослых", то есть пружина его я пыталась расшириться, и всякий раз "мир взрослых" заставлял его сжаться. Последняя его история была связана с любовной неудачей, то есть пружина его Я оказалась сжатой.
В настоящей точке мы прервёмся в связи ассоциацией, связанной с колебаниями, как свободными, так и вынужденными, поскольку психологическая жизнь едва ли не вся целиком состоит из всевозможных колебаний, и поэтому естественно попытаться получить самые первые представления и закономерностях, их характеризующих. Поэтому сейчас мы переходим к файлу "026.11.178112Колебания"