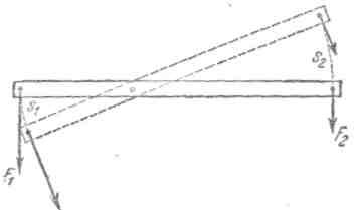
" Рис. 156. Сила,
действующая на левое плечо рычага, в n раз больше силы, действующей на
правое плечо. Перемещение s1, левого плеча
в n раз меньше перемещения s22 правого
плеча.
Например, если для равновесия рычага сила F1 должна быть в n раз больше, чем сила F (рис. 156), то при вращении рычага перемещение s1 его первого конца будет в n раз меньше, чем перемещение s2 второго конца. Для двойного блока такое же соотношение получается между силами, приложенными к веревкам, намотанным на оба блока и удерживающим его в равновесии, и перемещениями концов веревок при вращении блока. Это обстоятельство было сформулировано еще в древности следующим образом: «то, что мы выигрываем в силе, мы проигрываем в пути». Положение это имеет столь общее и вместе с тем столь важное значение, что оно получило название «золотого правила» механики.
Пользуясь введенными обозначениями, можем выразить «золотое правило» следующей формулой: или F1s1=F2s2.
При этом из «золотого правила» возникли важнейшие физические представления о работе и энергии. Вместе с тем «золотое правило» механики явилось первой простейшей формулировкой одного из основных законов природы — закона сохранения энергии, который оказался справедливым для всех без исключения явлений в природе".
Силу непосредственно мы увидеть не можем. Мы можем почувствовать силу, воздействующую на нас, но не увидеть. Судить о существовании силы мы можем по её проявлениям в движении. Поэтому и высказываться о силе непосредственно мы не можем, но - лишь опосредованно
«Золотое правило» механики практически соблюдается только в тех случаях, когда движение простых машин происходит равномерно, или с малыми ускорениями. Например, при вращении двойного блока концы веревок, навитых на скрепленные между собой блоки радиусов r1 и r2, переместятся на расстояния s1 и s2, пропорциональные этим радиусам: s1/s2 = r1/r2
Значит, для того чтобы «золотое правило» было справедливо для двойного блока, должно быть выполнено условие F1/F2 = r2/r1
Тогда силы F1 и F2 уравновесятся и, значит, машина должна либо покоиться, либо двигаться равномерно. Но для того, чтобы привести в движение двойной блок, нужно нарушить равновесие, прибавив к одной из сил, например к F1, некоторую силу f
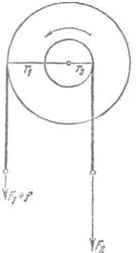(рис. 157). Возникающее движение
будет ускоренным (напомним, что, по нашему предположению, трение
отсутствует). При этом (F1+f) s1>F2s2—при
движении двойного блока с ускорением «золотое правило» не соблюдается. Но
чем меньше сила f по сравнению с F1, тем
ближе друг к другу произведения силы на путь для обоих концов блока и тем
меньше отклонение от «золотого правила». При очень малых f движение будет
происходить с очень малым ускорением, т. е. будет близко к равномерному.
Здесь мы видим, как мы спотыкаемся на третьем законе Ньютона, гласящем, что действие равно противодействию де всегда. Возникает вопрос: а когда одна сила больше другой, в чем это проявляется, и это при том, что действие равно противодействию? это проявляется в изменении движения либо состояния (внутренних напряжений) взаимодействующих тел. Это - первое. И второе заключается в существовании переходного процесса от одной формы равновесия к другой. Работа есть произведение силы на перемещение при условии, что направления силы и перемещения совпадают.
Таким образом, когда точка приложения силы перемещается, то сила совершает работу. Если перемещение происходит в направлении действия силы, то сила совершает работу, равную произведению силы на перемещение. Если же, несмотря на действие силы, перемещение точки приложения силы не происходит, то сила никакой работы не совершает. Например, если какой-либо груз неподвижно висит на подвесе, то действующая на него сила тяжести не совершает работы; но при опускании или падении груза эта сила работу совершает. Если сила тяжести груза равна Р и груз опустился на расстояние h, то работа силы тяжести равна Ph.
Понятие работы, не совпадает с инстиктивным понятием работы. В физике понятие работы связывают с перемещением тела. Инстинктивное понятие работы связывают с расходованием сил, энергии безотносительно к перемещению: удерживание тела нитью вызывает напряжение в нити, которое зависит от веса тела и свойств нити и может быть большим или меньшим. Инстинкт нам говорит, что при этом совершается работа: в нити вследствие существующих напряжений происходят медленные, постепенные разрушительные процессы, которые в конечном счете приведут к обрыву нити. С этой точки зрения физическое понятие работы оказывается условным и узким; хотя, с другой стороны, при натяжении нить растягивается постепенно всё больше и больше, и с этой точки зрения также имеет место движение, то есть имеет место всё тот же количественный процесс, хотя и в отношении порядка сильно различающийся.
Но дело, может быть, даже и не в этом, а в том, что под работой подразумевается расход энергии на преобразование чего-то. И тогда работа включает в себя два компонента: расход энергии ради преобразования чего-то во что-то. И тогда можно говорить о коэффициенте полезного действия совершаемой работы. В то же время, с инстинктивным понятием работы связывается принцип целесообразности как преобразования чего-то во что-то. Т.о. в инстинктивном понятии работы присутствует сильный субъективный компонент.
Когда перемещение происходит в направлении, перпендикулярном к направлению силы, то сила не влияет на перемещение в этом направлении; поэтому мы считаем, что в этом случае сила не производит никакой работы: если сила и перемещение перпендикулярны друг к другу, то работа силы равна нулю.
Это имеет место потому, что в этом случае отсутствует целесообразная составляющая работы. Сила действует, но не действует, поскольку изменений не происходит. В этом смысле выполненная работа - это работа, осуществившая преобразование. Если вы просто затрачиваете свои силы на что-то, то это не рассматривается в качестве работы, поскольку нет никакого другого результата, кроме траты энергии.
Мы определили работу силы в двух специальных случаях: когда перемещение точки приложения силы совпадает по направлению с силой и когда оно перпендикулярно к силе. В первом случае работа равна произведению силы на перемещение, во втором — равна нулю.
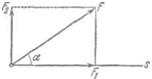
Теперь найдем выражение для работы силы в общем случае, когда перемещение s образует произвольный угол а с направлением силы F (рис. 159).
Для
этого разложим силу F на две составляющие: F1,
направленную вдоль перемещения (и равную проекции силы F на направление
перемещения s), и F2, направленную
перпендикулярно к s. Работа силы F1
совпадающей по направлению с перемещением s, равна F1s;
работа силы F2, перпендикулярной к
направлению s, равна нулю. Принимая работу равнодействующей равной сумме
работ составляющих, находим, что работа А силы F на перемещении s есть
A=F1s,
(90.1) т. е. работа силы равна проекции силы на направление перемещения
точки ее приложения, умноженной на величину перемещения.
Так как проекция любого отрезка на какое-нибудь направление равна длине отрезка, умноженного на косинус угла между отрезком и этим направлением, то F1=F cos а. Следовательно, работа А силы F при перемещении s равна А = Fs cos а. (90.2) Рис. 159. Разложение силы F на составляющие вдоль перемещения s (сила F1) и перпендикулярно к нему (сила F2).
Но величина s1=s cos а равна проекции перемещения на направление силы; значит, из формулы (90.2) следует еще одно соотношение для величины произведенной работы: А= Fs1, (90.3) т. е. работа силы равна проекции перемещения точки ее приложения на направление силы, умноженной на величину силы. Формула (90.2) включает рассмотренные выше частные случаи. Когда направления силы и перемещения совпадают, а=0 и cos a=1, так что работа равна A=Fs. Когда же сила и перемещение перпендикулярны друг к другу, то а=90° и cos a=0, так что и работа равна нулю.
Если попытаться перевести это на пальцы: есть движущееся тело, на которое действует сила под некоторым углом. В общем случае должны измениться и направление движения тела, и его скорость. Если теперь мы допустим, что направление движения тела каким-либо образом фиксируется. Тогда как это должно выглядеть в психологическом плане? Пусть существует какая-то рациональная фиксация тела, допускающая действия только в каком-то определенном направлении. Тогда нормальная составляющая в явлении не произведет работы как внешне воспринимаемой вещи, но при этом действие нормальной составляющей будет оказываться разрушающее воздействие на саму рационализацию, которой фиксируется определенное направление движения тела.. Однако если подобного рода рациональных установок нет, то эффект действия силы будет зависеть от массы тела. Теперь о порядке действия силы в психологическом аспекте: никакая реакция тела невозможна без предварительного изменения состояний напряжения самого тела. В этом смысле тело оказывается подобно сжимаемой пружине: для того, чтобы разжаться, пружина должна быть предварительно сжата, как и, напротив, для того, чтобы сжаться, пружина предварительно должна быть разжата. В таком случае от массы тела зависит степень возникающего в нём напряжения. Помимо этого, в рассмотрение свойств массы тела должны входить его объём и плотность и, далее, плотность на единицу объёма.
Сила совершает работу, если перемещение точки приложения силы происходит в направлении действия силы. Если же это перемещение происходит в направлении, противоположном направлению действия силы, то мы говорим, что совершается работа против данной силы. Например, если на нерастянутую пружину мы подвесим груз (рис. 160) и дадим ему возможность опускаться, то сила тяжести, действующая на груз, совершит работу, так как груз движется в направлении этой силы. В то же время пружина растягивается и совершается работа против силы упругости пружины. Рис. 160. При опускании груза совершается работа против силы натяжения пружины F. Для того чтобы различать работу, совершаемую силой, и работу против силы, работе можно приписать знак; будем считать работу, совершаемую силой, положительной, а работу, совершаемую против действия силы, — отрицательной. При опускании груза работа силы тяжести положительна, а работа силы упругости пружины отрицательна. Условие о знаке работы будет выполнено само собой, если приписывать одинаково направленным перемещениям и силам одинаковые знаки, а противоположно направленным перемещениям и силам — разные знаки. Подобно этому при силе, составляющей произвольный угол с перемещением, будем считать знаки перемещения и компоненты силы вдоль перемещения одинаковыми или разными в зависимости от того, направлена ли компонента силы по перемещению или противоположно ему. Формула (90.2) годится и для того случая, когда совершается работа против силы. В самом деле, тогда угол а между силой и перемещением больше 90°, cos а делается отрицательным и работа получается отрицательной. Если на движущееся тело действует только одна сила, то, когда эта сила совершает положительную работу, скорость тела растет. Действительно, в этом случае сила, а значит, и ускорение направлены по скорости, увеличивая ее. Если же сила совершает отрицательную работу, ускорение направлено против скорости и скорость тела убывает.
Рис. 160. При опускании груза совершается работа против силы натяжения пружины F.
Для того чтобы различать работу, совершаемую силой, и работу против силы, работе можно приписать знак; будем считать работу, совершаемую силой, положительной, а работу, совершаемую против действия силы, — отрицательной. При опускании груза работа силы тяжести положительна, а работа силы упругости пружины отрицательна.
Условие о знаке работы будет выполнено само собой, если приписывать одинаково направленным перемещениям и силам одинаковые знаки, а противоположно направленным перемещениям и силам — разные знаки. Подобно этому при силе, составляющей произвольный угол с перемещением, будем считать знаки перемещения и компоненты силы вдоль перемещения одинаковыми или разными в зависимости от того, направлена ли компонента силы по перемещению или противоположно ему.
Формула (90.2) годится и для того случая, когда совершается работа против силы. В самом деле, тогда угол а между силой и перемещением больше 90°, cos а делается отрицательным и работа получается отрицательной.
Если на движущееся тело действует только одна сила, то, когда эта сила совершает положительную работу, скорость тела растет. Действительно, в этом случае сила, а значит, и ускорение направлены по скорости, увеличивая ее. Если же сила совершает отрицательную работу, ускорение направлено против скорости и скорость тела убывает.
Особенность настоящего рассуждения состоит в том, что мы имеем дело с двумя противоположными сторонами, и при этом оказывается, что в рассуждении одна из сторон полагается, другая - предполагается. Иными словами, мы говорим об одной стороне с таким видом, как будто другой стороны при этом не существует. Мы говорим о работе, которую произвела гиря, и ничего не говорим о равной и противоположной ей работе пружины. Эти две работы оказываются одинаковыми, но с разными знаками. Но отождествляем мы себя, как правило, только с одной из сторон, так как в противном случае возникает своего рода стопор. Здесь, именно в этом состоит тайна взаимоопределения противоположностей, когда одна из сторон противоположности оказывается снятой и, тем не менее, "светится" в другой стороне противоположности. Мы рассматриваем вес гири и её движение и уже определение её свойств в снятом виде содержит свойства противоположной стороны. Но благодаря чему это становится возможным? - благодаря существующему третьему - притяжению земли, тому, что гиря обладает весом. Ведь в невесомости гиря не обладала бы весом и никак не воздействовала бы на пружину. Т.о., гиря оказывается между двумя объектами - между землей, воздействие которой отражается в форме веса, и свойствами к растяжению пружины, величиной её упругости. Но вес гири обусловлен её массой, включающей в себя плотность и объём, то есть своеобразное количество материи.
Соответственно, в связи с количеством материи, можно говорить о количестве духа субъекта как показателе его реакции на воздействия.
Из сказанного видно, что, во-первых, мы всегда имеем дело с противоположностями, и, во вторых, мы всегда отождествляем себя с какой-то одной из этих сторон, и противопоставляем, противополагаем себя другой стороне. Итак, отождествление с одной стороной является причиной либо следствием противопоставления другой стороне.
Так как работа определяется произведением силы на перемещение, то за единицу работы следует принять работу, совершаемую силой, равной единице, при перемещении точки ее приложения в направлении действия силы на расстояние, равное единице.
В системе СИ единицей работы служит работа силы в 1 н при перемещении на 1 м. Эта единица носит название «джоуль» и обозначается дж1).
В системе СГС единицей работы служит работа, которую совершает сила в 1 дн при перемещении на 1 см. Эту единицу работы называют «эрг». Так как 1 н=105 дн, а 1м=102 см, то
1 дж = 1 • 107 эрг.
В системе единиц МКСС за единицу работы следует принять работу, которую сила в 1 кГ совершает при перемещении на 1 м. Эта единица работы носит название «килограммометр» (кГм). Из соотношения 1 кГ =9,8 н заключаем:
1 кГм = 9,8 дж.
При грубых расчетах можно полагать
1 кГм = 10 дж.
Понятие работы позволяет по-новому подойти к «золотому правилу» механики. Обратимся снова к двойному блоку и предположим, что при помощи силы, прикладываемой к концу одной из веревок, производится поднятие некоторого груза, подвешенного к концу второй веревки. Как мы видели, для концов обеих веревок произведения силы на перемещение равны. С другой стороны, сила, действующая на первую веревку, и перемещение конца этой веревки совпадают по направлению. Точно так же совпадают направления перемещения гири и силы, действующей на нее со стороны второй веревки. Значит, работа, совершаемая силой, приложенной к первой веревке, равна работе, совершаемой над гирей со стороны простой машины. Таким образом, двойной блок не создает работы и не приводит к исчезновению работы, а лишь передает ее. В то же время суммарная работа, совершаемая над простой машиной, оказывается равной нулю: действительно, для сил, приложенных к веревкам, направления силы и перемещения совпадают для одной веревки и противоположны для другой, т. е. равные по величине работы имеют противоположные знаки и при сложении уничтожают друг друга.
Это положение оказывается справедливым для всех простых машин, как для случаев, когда направления сил и перемещений совпадают, т. е. для случаев, когда применимо «золотое правило», так и для случаев, когда они не совпадают и «золотое правило» не применимо.
Таким образом, мы приходим к принципу более общему, чем «золотое правило»: во всякой простой машине, движущейся равномерно, работа передается без изменения, т. е. работа, которую совершает машина, равна работе силы, приводящей машину в движение. Это положение получило название: принцип сохранения работы.
Необходимо иметь в виду, что принцип сохранения работы не будет выполнен, если простая машина деформируется при передаче работы, например, если рычаг сгибается или веревки полиспаста растягиваются. В самом деле, если попытаться поднять большую тяжесть, применив в качестве рычага гибкий прутик, то, совершив на длинном конце рычага определенную работу, мы даже не стронем с места груз, лежащий на коротком плече, на котором, следовательно, произведенная работа будет равна нулю: единственным результатом будет то, что рычаг согнется. Подобно этому, заменив в блоке веревку легко растягивающейся резинкой и попытавшись поднять с земли большой груз, мы произведем работу, растягивая резинку с одного конца, но второй конец резинки, привязанный к грузу, который так и останется лежать на месте, никакой работы не произведет. И здесь единственным результатом будет деформация механизма. Если взять более жесткий рычаг или более толстую резинку, то поднять груз на некоторую величину может быть и удастся. Однако работа, произведенная на втором конце нашей машины, будет в этом случае меньше, чем работа, производимая приложенной силой,— «золотое правило» и принцип сохранения работы будут нарушены. Поэтому в дальнейшем будем считать, что все простые машины изготовлены из несгибаемых рычагов, имеют нерастяжимые веревки и т. д. Тогда принцип сохранения работы будет выполнен.
Принцип сохранения работы дает возможность удобного расчета сил в простых машинах. Например, в полиспасте с п витками веревки (рис. 146) конец веревки, за который тянут рукой, перемещается больше, чем крюк, тянущий груз. Действительно, при перемещении руки на длину s подвижная часть блока поднимается на высоту в n раз меньшую, так как изменение длины веревки распределяется на п ее участков между блоками. Следовательно, на основании принципа сохранения работы мы можем утверждать, что сила, приложенная к концу веревки, должна быть в n раз меньше, чем сила, приложенная к крюку (весом подвижной группы блоков мы пренебрегаем). Этот результат мы получили выше (§84) непосредственно из рассмотрения сил.
Из сказанного открывается своего рода тайна отношений между противоположностями, которая говорит о передаче энергии от одной стороны противоположности к другой (закон сохранения энергии). Но это становится возможно благодаря введению противоречия в понятие равномерного движения, которое является таковым всегда лишь с некоторым допуском, то есть считается, что данное неравномерное движение является равномерным, в нём, т.ск., процент неравномерности относительно невелик сравнительно с процентом равномерности. В связи с этим, конечно, возникает вопрос о том, как вычисляются сами эти проценты.
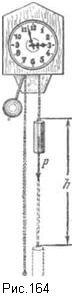
Простые машины обладают способностью совершать работу, но не могут «запасать» эту способность, так как одновременно с тем, как они получают ее на одном конце, они отдают ее на другом. Однако во многих случаях тела могут накоплять «про запас» способность совершать работу, и часто строят специальные механизмы, способные запасти работу, а затем отдать ее. Типичным примером является гиревой завод стенных часов (рис. 164). Подтягивая гирю вверх, мы совершаем некоторую работу. В результате часовой механизм получает способность совершать в течение длительного времени работу, необходимую для хода часов, т. е. для поддержания движения всех колес, стрелок и маятника, испытывающих сопротивление движению, вызванное трением. По мере хода часов гиря постепенно опускается и запас работоспособности механизма уменьшается. Через некоторое время понадобится снова «завести» часы, т. е. вновь сделать их способными к совершению работы, требующейся для их хода.
Рис. 164. Поднятая гиря обладает запасом работы, который постепенно расходуется на поддержание движения часов.
При заводе часов гиревой механизм накапливает способность производить работу; по мере хода часов способность производить работу расходуется. Поднимая груз, мы запасаем работу; опускаясь, груз способен производить работу. В теле можно «запасать работу» не только путем поднятия тела на некоторую высоту. Деформируя тело, например сжимая или растягивая пружину, мы производим работу; в результате деформированное тело получает способность совершать работу. Работу совершает «заведенная», т. е. деформированная, пружина ручных или карманных часов, «пружинный двигатель» заводных игрушек и т. д.
Сообщая скорость какому-либо телу, также приходится затрачивать работу; в результате тело приобретает способность совершать работу, уменьшая свою скорость. Например, железнодорожный вагон, подтолкнутый паровозом к составу, останавливаясь, сжимает пружины буферов; пуля, попадающая в препятствие, производит работу разрушения материала, и т. д.
Во всех разобранных случаях работа производится при изменении состояния тела: при опускании груза, при раскручивании пружины, при остановке движущегося тела. Пока эти изменения еще не наступили, работа не произведена; в теле имеется некоторый запас еще не совершенной работы. При совершении работы этот запас расходуется. Производя же работу над телом: поднимая его вверх, деформируя его, сообщая ему скорость,— мы сообщаем ему запас работы, который в дальнейшем можно использовать, возвращая тело в исходное состояние.
Запас работы, которую может совершить тело, изменяя свое состояние, называют энергией.
К механическим видам энергии относятся: энергия, связанная с поднятием тела над землей (и вообще энергия, связанная с силами всемирного тяготения); энергия, связанная с деформациями тела; энергия, связанная с движением тела. Изменение энергии определяется той работой, которую надо совершить, чтобы вызвать это изменение. Следовательно, измерять энергию следует в тех же единицах, в которых измеряют работу, т. е. в джоулях в системе СИ, в эргах в системе СГС и в килограммометрах в системе МКСС.
Эта схема очень хорошо работает на человеческих рефлексах: что-то нас возмутило, и мы начинаем разряжаться. Или, напротив, мы начинаем "заводить" сами себя в связи с каким-то событием с тем, чтобы адекватно реагировать на него. Поэтому можно говорить как об актуализации, так и работе рефлексов, и мы вполне можем анализировать рефлекторную работу с этой точки зрения.
Найдем, чему равна работа А, совершаемая при подъеме тела весом Р на высоту h. Будем считать, что поднятие тела происходит медленно и что силами трения при подъеме можно пренебречь. Мы уже знаем (§ 94), что произведенная работа против силы тяжести не будет зависеть от того, как мы поднимаем тело: по вертикали (как гирю в часах), по наклонной плоскости (как при втаскивании санок в гору) или еще каким-либо способом. Во всех случаях эта работа будет равна А = Рh. При опускании тела на первоначальный уровень сила тяжести произведет такую же работу, какая была затрачена на подъем тела. Значит, поднимая тело, мы запасли работу, равную Ph, т. е. поднятое тело обладает энергией, равной произведению веса тела на высоту поднятия.
Эта энергия не зависит от того, по какому пути происходил подъем, а определяется лишь положением тела (высотой, на которую оно поднято). Поэтому эту энергию называют энергией положения. Чаще ее называют потенциальной энергией.
Итак, потенциальная энергия Еп тела, поднятого на некоторую высоту, выражается формулой
Eп = Ph. (97.1)
Так как вес тела можно выразить через его массу m и ускорение свободного падения g формулой Р = mg, то мы можем потенциальную энергию, запасенную телом массы т, поднятым на высоту h, выразить еще и так:
Eп = mgh. (97.2)
При данном исходном положении тела величина работы, которую может совершить тело, т. е. потенциальная энергия, зависит от того, насколько тело может опуститься. В гиревом механизме это определяется длиной цепочки, на которой висит гиря, в примере с наклонной плоскостью — высотой наивысшей точки наклонной плоскости над ее наинизшей точкой. В других случаях наинизший уровень не может быть так естественно определен. Например, если тело лежит на столе, то можно определять его потенциальную энергию той работой, которую оно совершило бы, опускаясь до пола, до уровня земли или до дна погреба и т. д. Поэтому нужно условиться заранее, от какого уровня отсчитывать высоту, а вместе с тем и потенциальную энергию тела. Выбрать этот уровень можно совершенно произвольно, так как во всех физических явлениях всегда бывает важна не сама потенциальная энергия, а ее изменения, которыми определяется совершаемая работа. Изменения же потенциальной энергии будут, очевидно, одинаковыми, какой бы мы ни выбрали исходный уровень.
Обычно уславливаются считать потенциальную энергию тела, лежащего на поверхности земли, равной нулю.
Т.о., энергетический потенциал между телами рассматривается в качестве нулевого в случае совмещения тел. Энергетический потенциал, отражающий взаимодействие тел, возникает по мере увеличения расстояния между ними. В психологии мы имеем то же самое: полное совпадение взглядов даёт отсутствие энергетичесих процессов. Последние возникают по мере нарастания противоречия между взглядами.
07.09.08 г.