на главную страницу
визитка
темы

4. Единицы
   (первая версия)

   1.

   В разделе 3 "Корни" был высказан принцип линейности, который заключался в том, что в результате операций над объектами мы получали объекты того же качества, а все объекты располагались в определенном порядке один за другим, так что всегда можно было определить, какой объект следует за другим или ему предшествует. Т.о., мы имеем дело со свойством  линейности как выражением  последовательного способа упорядоченности объектов.
      Линейность является  частным случаем пространственного   расположения объектов как формы их порядка.
       Рассмотрение объектов может быть начато с отдельного объекта, который можем назвать точкой. Линейное расположение точек порождает линию. Само понятие линии характеризуется непрерывностью, как понятие объекта - дискретностью. Переход от точки к линии требует сохранения дискретности в непрерывности, то есть выражения непрерывности через дискретность. Это достигается введением единичного отрезка, характеризующего линию. Непрерывность проявляет себя в том, что единица способна делиться бесконечным образом на множество более мелких единиц, как и возможно бесконечное формирование всё более крупных единиц на основе исходной. 

   2.Построение

     1 В качестве исходного понятия нам даны точки. Точки мы можем интерпретировать как отдельные объекты и соотносить с ними натуральный ряд чисел и, пожалуй, целые числа, то есть числа,  включающие в себя ноль и отрицательные числа.
      2 Из точек мы можем строить линии подобно тому, как  можем образовывать ряды из объектов. Мы получаем собственно линию, осуществляя предельный переход, устремив величину точки к бесконечно малой. Т.о. мы получаем ряд действительных чисел, которые образованы именно за счет предельного перехода. Ряд действительный чисел - это одномерные числа. Переходя к плоскости, мы переходим к количественному выражению её точек посредством нового вида единиц - квадратов, и, соответственно, получаем новые числа, двумерные, т.к. соответствующие единицы плоскости могут быть представлены только двумя одномерными числами. Переходя к объёмам, мы переходим снова к иным, трёхмерным единицам, так как единицей измерения становится куб, а точка в трёхмерном пространстве обозначается тремя цифрами. И т.о. мы для n-мерного пространства получаем n-мерные числа.
       Переход от понятия линии к плоскости, от плоскости - к трёхмерному пространству и от него - к n-мерному всякий раз связан с изменением порядка объектов и операциями, связанными с порядками, которым они соответствуют. Если представить всё это в виде конечных объектов, то каждому виду пространства будут соответствовать свои единицы. Точечные объекты описываются натуральным рядом чисел, дискретами, линейные - единичными отрезками, плоскости - единицами площади - квадратами, 3-мерное пространство - объемами - единичными кубами и т.д.. При этом оказывается, что всякое пространство высшего порядка выражается через пространства низшего порядка.
      Если представить себе, что линия состоит из единичных (не делимых) объектов-отрезков, то линия редуцируется в натуральный ряд чисел. Затем, следует иметь ввиду, что когда мы говорим о предельном переходе, то ведь это происходит только в нашей голове. На практике для нас точка всегда представляет... что? - какой-то объём. И т.о. оказывается, что мы начинаем с объёма чувственного и заканчиваем объёмом рациональным, так что начало и конец совпадают. Линия - это множество последовательно расположенных точек. Площадь - это множество последовательно расположенных линий, то есть последовательностей последовательностей точек , объём - это множество последовательно расположенных площадей, то есть последовательностей последовательностей последовательностей точек и т.д.. 
       Линии, т.о., у нас получаются за счет того, что мы считаем точки, квадрат - за счет того, что мы считаем линии, третья степень- за счет того, что считаем квадраты и т.д.
       Видимо, следовало бы ввести понятия объёма первого порядка - линии, 2-го порядка - площади, 3 порядка - собственно объём, , 4-го порядка и т.д.
       Переходя к новым единицам измерения, мы тем самым переходим к качественно новым числам, которые могут быть редуцированы в направлении своих составляющих.
      3. Мы переходим от натуральных чисел к действительным, осуществив предельный переход от конечных величин к бесконечным - бесконечно малым либо бесконечно большим. Оставаясь в сфере конечных объектов, имеем дело с различными объектами. Осуществив предельный переход, мы вступаем в область непрерывных объектов, в которых можем выделять какие угодно части, тем не менее, неразрывно связанные между собой.
      4. Осуществим  построение, как это предложено на рис.1. Назовём вводимые первично прямые -х0х, -у0у, -z0z координатными осями. В таком случае мы видим, что каждая точка линии -х0х может может применяться в качестве имени всех тех линий, которые её пересекают, в настоящем построении это бесконечное множество линий -у0у, -z0z. И подобное же утверждение можно сделать и относительно других координатных осей. Тогда, если следовать этой логике, каждая из плоскостей должна состоять из линий. Но через одну точку может быть проведено множество линий, и тогда мы получаем общее имя для множества объектов, обладающих тем свойством, что они проходят через общую им всем точку, и, следовательно, мы не можем по этому имени однозначно определить конкретную линию. Мы можем  говорить о собственном  имени линии лишь относительно линий, лежащих в одной плоскости, т.е.  параллельных друг другу. Значит, если имя х, то имя относительно линий у либо линий z, что можно выразить в виде у_х
    
      либо z_х. Тогда выражение вида х_z будет обозначать имя линии х на оси z и т.п.
      Но в таком случае точно такой же закономерности должно подчиняться и придание имен плоскостям, а именно, плоскость должна обозначаться при посредстве какой-то линии подобно тому, как посредством точки, принадлежащей некоторой линии, определяется собственное имя из класса линий, проходящих через точку. Так, мы пишем у_х или z_х, имея ввиду соответствующие координатные оси у либо z.
     Подобно тому, как мы из точек составляли линию, точно также из линий мы составляем точно такую же "линию", которую называем плоскостью. То есть это - линия, единицами которой непосредственно выступают не точки, а линии. И, значит, в этом случае мы должны иметь дело с уже именованным рядом линий для того, чтобы иметь имена для плоскостей.
       Тогда, имея дело с какой-то линией, например, у_х=2, посредством её мы можем обозначить одну из возможных плоскостей х(у_х=2) или z(y_x=2)
       Ведь согласно построению мы имеем три одинаковых перпендикулярных друг другу класса плоскостей: ху, хz, yz, причем, в каждом классе есть плоскости, через которые проходят оси координат, и такие плоскости являются нулевыми. Но через всякую линию может быть проведено, согласно построению рис.1, две перпендикулярные друг другу плоскости: одна плоскость параллельна  плоскости уz, другая параллельна плоскости ху. 
     Тогда мы получаем два различных  и единственных имени для двух  различных  плоскостей: ху.у_х=2 и yz.y_x=2 Но ху.у_х=2=у_х, и значение её может заключаться только в выражении смещения начальной точки отсчёта.
      Выражение yz.y_x=2 соответствует единичной плоскости, "надетой на шампур оси х", соответственно, выражение yz.y_x   представляет собой бесконечное множество подобных плоскостей, образующих пространство третьего порядка.
   
   
   
      Для прояснения образа полезно использовать понятие пачки. Можно считать, что мы во всех случаях имеем дело с пачками объектов. Пачка точек равна линии, пачка линий образует плоскость, пачка плоскостей образует объем. Пачка объёмов может быть приравнена к точкам, и тогда процесс начинается сначала, а с точкой мы теперь уже соотносим более сложное понятие, имея ввиду, что точка может быть одномерной, двумерной , трёхмерной и т.д.
   
      В построенной модели универсума на практике мы имеем дело с конечными величинами, и, соответственно, с какими-то интервалами значений переменных. Поэтому на практике  линии имеют конечные длины, плоскости - конечные площади, пространственные объекты - конечные объёмы.  И тогда важным становится вывод, что точка может быть не только одномерной, но и многомерной. Для целей наглядности допустим, что мы имеем множество консервных банок. В плоском ящике банки укладываются линейно  по 10 штук (линия) в пять рядов (плоскость) Ящики укладываются по десять штук друг на друга (объём) и увязываются стальными лентами (единица объёма = точка). На складе связки ящиков располагаются на площади по десять ящиков в длину (линии) и по пять в ширину (плоскости) и укладываются друг на друга в три ряда (объем)

   Т.о., мы  наблюдаем относительность применяемых понятий точки, линии, плоскости, объёма. Когда мы рассматриваем, например, в качестве единицы линию, то линия выступает для нас в качестве точки, то есть как целое,  несоставной объекта. И, значит, это относится к стороне, аспекту отражаемой реальности.
   
      07.08.08 г.

   5. Единицы (вторая версия)

   1.

   Проведем прямые -х0х, -у0у, -z0z, представляющие собой координатные оси декартовой прямоугольной системы координат, которая будет представлять собой своеобразные леса, на которых мы будем осуществлять наши построения.
   
       Объект может обозначать самого себя и может обозначать другой объект. Когда мы говорим: х – мы имеем ввиду объект, который обозначает сам себя, когда мы говорим у_х мы имеем ввиду, что объект х обозначает другой объект у. Т.о. два выражения х и у _x имеют одно и то же имя, но обозначают разные вещи. В первом случае точка обозначает точку, во втором случае точка обозначает линию. Объект, обозначающий сам себя, указывает на себя, объект, выступающий в качестве имени другого, указывает на другой объект. Поскольку имя объекта и он сам тождественны, мы имеем круг. Поскольку имя объекта указывает на другой объект, мы получаем ассоциативный способ употребления имён, который для своей однозначности требует каких-то дополнительных данных.
      Т.о. мы получаем, что у нас при ассоциативном употреблении х указывает на линию, и это выражается нами в форме у_x=а, а выражение у_х указывает на произвольную линию у плоскости ух. Тогда, представив, что х последовательно принимает в выражении у_х возможные значения, и рассматривая полученный результат как актуализированное х, мы получим, что у_х представляет плоскость. Действительно, ведь когда мы пишем у=f(x), то мы представляем себе образ функции в целом, а не отдельные её значения. Поэтому интерпретация выражения у_х не выходит за пределы принятой на практике математической традиции, и мы можем записать ух=у_х.
   
   
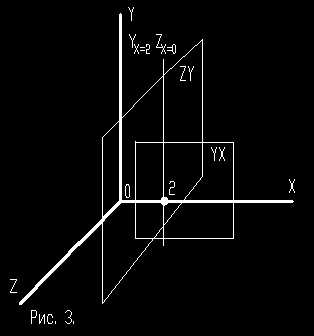
      Рассмотрим построение  рис.3. Через линию у_х=2 можно провести бесконечное множество плоскостей, но в связи с наложенными  ограничениями можем провести плоскость yz=z(y_x=2), где выражение у_х=2 является именем плоскости плоскости zy . Если систему координат записывать в виде хуz, то 2уz будет обозначать плоскость уz, проходящую через точку х=2; выражение х2z будет обозначать плоскость хz в точке у=2, выражение ху2 будет обозначать плоскость, проходящую через точку z=2
      Недостаток этого способа представления состоит в том, что им не указывается направление линий, образующих плоскость. Действительно, два выражения у_х и х_у обозначают, по-видимому, "одну и ту же плоскость ху, но это- плоскости с различным направлением образующих их линий и поэтому это - разные плоскости. Условно это можно было бы записать так: ух=у_х  , ху=х_у
      Коды NTML не позволяют строить выражения с индексами, которые,  в свою очередь,  содержат индексы, поэтому примем, что последовательность вида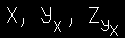 выражается последовательностью х, yx, zyx, которая  обозначает бесконечное множество  плоскостей  zy.
       Действительно, пусть х=2, тогда у_х=2  есть линия, параллельная координатной оси у, а у_х - это
   бесконечно множество таких линий, образующих плоскость ух. Через каждую из этих линий можно провести бесконечное множество плоскостей. Согласно построению, плоскости должны быть параллельны координатным плоскостям. Поэтому через каждую линию можно провести только одну плоскость, параллельную  координатной плоскости zу. Поэтому через множество линий у_х можно провести бесконечно множество параллельных плоскостей, образующих 3-мерное пространство.
     Мы можем осуществить подобного же рода построения, осуществив иные последовательности при построении. Вместо последовательности х, ух, zух можем взять последовательности х, xz, xzy, либо у, yx, yxz, либо у, yz, yzx, либо z, zx, zxy, либо z, zy, zyx. При этом будет изменяться значение употребляемых имен.
   
     Из сказанного следует, что   имя объекта А  при посредстве объекта имени объекта В обозначается индексным выражением, в котором в качестве индекса выступает объект В: А_В
   
      Отсюда получаем формы записи: выражение у_х=2=3 обозначает точку 3 на линии 2 координаты у.
   
      Итак, изначально мы имеем дело с объектами одного уровня. Мы произвольно определяем субординацию между объектами, определяя их  относительно друг друга в качестве объектов высшего и низшего уровня. Приняв одну из координатных осей за отправную, мы тем самым определяем точки на ней в качестве указателей (собственных имен) на тиражируемые параллельные линии второй оси, которые образуют объект следующего уровня – плоскость и т.д.<
   
      10.08.08 г.