-
Как были получены мнимые числа?
Сначала было введено сложение.
2+2=4
Затем умножение, которое по существу тоже является сложением.
2х3=2+2+2
Затем возведение в степень, которое по существу тоже является сложением.
2в тр.ст.=2х2х2=2+2+2+2
Затем или одновременно с этим, не знаю хронологическую последовательность, были введены отрицательные и положительные числа.
Далее начали оперировать с новыми числами.
Условились, что
(-5)х(-5)=+25
(+5)х(+5)=+25
(-5)х(+5)=-25
Таким образом
(-5)х(-5)=+25
(+5)х(+5)=+25
То есть положительное число, умноженное само на себя, дает положительное число.
Отрицательное число, умноженное само на себя, дает положительное число.
Числа, которое при умножении само на себя, дает отрицательное число, нет.
Корень из положительного числа может быть и положительным, и отрицательным.
Извлекать корень из отрицательного числа бессмысленно.
Тем не менее математики решили извлечь корень из отрицательного числа. Возможно, они исходили из глубокой мысли, что поскольку в математике есть и отрицательные числа, и знак корня, их надо совместить из этого непременно выйдет толк.
Извлечь корень из отрицательного числа, то есть найти, какое число, умноженное само на себя, дает отрицательное число, не удалось, так как математики сами условились, что таких чисел нет.
Тогда математики сделали, что могли.
Представили отрицательное число в виде произведения положительного числа на -1, извлекли корень из положительного числа, надеясь, что проблема таким образом упростится и что с -1 они что-нибудь придумают.
кор.из(-25)=кор.из/(+25)(-1)/=кор.из(+25)хкор.из(-1)= +-5хкор.из(-1)
Осталось совсем немного.
Извлечь корень из -1.
Однако найти какое число, умноженное само на себя, дает -1 не удалось по той же самой причине.
Но если нельзя найти, то можно обозначить кор.из(-1) через i.
Таким образом,
кор.из(-25)=+ -5хкор.из(-1)=+ -5i
То есть корнями из -25 являются +5i и -5i.
Эти результаты были названы мнимыми числами.
Надо сказать, что хотя i внушает больше доверия, обозначает оно ничто иное, как кор.из(-1).
Разница в том, что когда пишут -1, достаточно очевидно, что математикам не удалось ни найти, какое число, умноженное само на себя, дает кор.из(-1), ни разумно объяснить ситуацию, а когда пишут i, эта проблема завуалирована.
Найти число не могут потому, что сами договорились, что таких чисел нет.
- Сложение и умножение
-
Последуем за А.А.:
Сложение: 2+2. Например, двое ножниц и две овцы. Если это просто объекты, то получаем 4. Но если учитывается качество объектов, то сложение теряет смысл, т.к. мы имеем дело с разными, не пересекающимися множествами. Единственное, что здесь можно добавить, хотя это относится к другой идее, что если ножницы предназначены для стрижки овец, то можно говорить об установлении соответствия между овцами и ножницами и, в частности, об установлении соответствия между мощностями двух множеств. Но это уже из другой оперы. Мы видим, что для того, чтобы иметь возможность складывать элементы двух множеств, нужно подвести их по общий род. Складываться могут только объекты одного рода, так как только в этом случае мы имеем дело с количественным отношением.
Умножение: 2*3=6. Умножение сводится к сложению: 2+2+2 либо 3+3 Мы видим, что слагаемые в приведенных примерах играют разную роль: одно слагаемое выступает в качестве множества, представляющего объекты какого-то рода. Второе слагаемое указывает на то, сколько раз следует взять множество. То есть второй элемент как бы элемент, производящий множества одного рода, элементы которых складываются. В результате мы получаем мощность нового множества, включающего в себя все элементы исходного множества. Например, человек в неделю получает 100 долларов. Сколько он получит в месяц? в год?
Увеличение числа слагаемых ничего не меняет в сути дела: всегда есть множество исходных объектов, которые тиражируются сколько-то раз, получается новое множество, включающее в себя все элементы тиражированных множеств. Полученное множество в свою очередь тиражируется сколько-то раз, получается новое множество, и т.д.
Умножение сравнительно со сложением характеризуется тем, что занимается сложением объектов одного и того же тиражируемого множества. То есть если сложение допускает сложение разных по мощности множеств одного рода, то умножение имеет ввиду одно и то же множество. Например, дневной рацион питания солдат заключает в себе столько-то граммов животных жиров, мяса, круп и т.д.. Теперь это множество тиражируется по числу солдат, и каждый из элементов полученного множества множеств ставится в соответствие с каждым элементом множества солдат. Что отсюда мы получаем? - умножение двух множеств, таких, что каждому элементу одного множества ставится в соответствие множество элементов другого растиражированного множества. Если мы в связи с этим введем принцип соответствия, то - элементы одного множества ставятся в соответствие множеству свойств элементов другого множества, в данном примере - суточный рацион питания солдата определяется его потребностями в пище, и мы получаем, что содержание суточного рациона солдата образовано на основе потребностей его организма в питательных веществах. В свою очередь, множество солдат существует постольку, поскольку оно создается в соответствии с потребностями, то есть свойствами другого множества, и т.д.
Пусть есть два множества элементов А, В. Множество А={a1, a2, a3} B = {b1, b2}. В обоих множествах элементы ai, bj, где i=1,2,3, j=1, 2 - отдельные объекты, следовательно, суть единицы, поэтому в самой записи множества можно указать на операцию сложения как получение его мощности. Тогда множества перепишутся так: А={a1+ a2+ a3} B = {b1+ b2}, а умножение даст: C= A* B = a1 * (b1+ b2) +a2 * (b1+ b2) + a3 * (b1+ b2) = {a1b1 + a1b2 + a2b1 + a2b2 + a3b1 + a3b2} Очевидно, что мощность множества mA=3, множества В mB=2, а произведение равно 6. Однако мы видим, что технология получения произведения не является совсем простой.
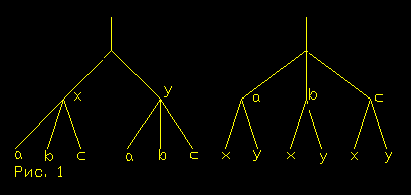
На рис.1 показано, что технологический процесс умножения может быть представлен в форме дерева, если исходить из данной нами выше интерпретации умножения. Но в то же самое время из множества путей дерева видно, что в результате умножения мы получаем сложные объекты, представляющие собой некий симбиоз множеств, так как элементы a1b1, a1b2 и т.д. - ведь это не простая форма соответствия между элементами множеств, но это прежде всего отношение принадлежности одних элементов другим элементам, причём, это отношение может быть взаимным, как при умножении, что показано на примере деревьев рис.1. Между тем, в самом результате умножения мы не обнаруживаем ничего, кроме простого неопределенного тиражирования исходных объектов и их суммирования, которое и даёт нам искомый результат умножения; в нем не показывается, по отношению к чему получается такой результат.
Если условно принять, что умножение выполняется последовательно слева направо и первое слагаемое представляет исходное множество элементов, над которыми производятся операции, то все последующие сомножители указывают на число множеств тиражируемых элементов. В этом случае мы получаем последовательное построение дерева снизу вверх.
Но во всех этих случаях знака чисел практически нет, потому что о положительном числе можно говорить только тогда, когда есть отрицательное число, причем, по большому счету, нет как такового положительного и отрицательного, а есть противоположные числа. Отрицательное же и положительное в субъективном смысле - это уже относится к интерпретациям чисел. С другой стороны, понятие отрицательных и положительных чисел также может рассматриваться как как непрерывное движение от минус к плюс бесконечности, и тогда может быть введено понятие начального условия как своеобразного производного (относительного) ноля, который может быть совмещен с любым числом абсолютного ряда чисел от минус до плюс бесконечности с его абсолютным положением ноля, как и всех других чисел..
- Объект и признак
- В логике есть правило: признак
признака предмета есть признак самого предмета. Я хочу здесь обратить ваше
внимание на относительность понятий объекта и его признака.
Объект является через свои признаки. Если рассматривать объект как вещь, которая обладает множеством признаков, то можно осуществить по отношению к нему мыслительную операцию вычитания из него каких-то признаков, либо же мы можем добавлять ему какие-то признаки, при этом объект будет изменяться. Объект является нам через свои признаки. Объект - это как бы (материальный) носитель признаков, с другой стороны, признак - это некая определенность, некоторая способность, свойство объекта. Т.о. объект и его признак - это противоположные стороны одного и того же. За признаком мы видим объект, объект же заявляет нам о своём существовании через признаки, которыми он обладает. Поэтому в качестве положенной стороны мы можем брать одну либо другую сторону. Это значит, что признак мы можем рассматривать как объект, объект - как совокупность признаков.
А если так, то мы можем о каком-то свойстве объекта говорить как об объекте. Поэтому мы имеем право рассматривать признаки сами по себе как объекты постольку, поскольку в любом случае их реальностью являются последние. В качестве такого объекта будем рассматривать числа. Тогда объекты a1 и т.п. будут выступать для нас в качестве каких-то определенных чисел.
- Законы сложения и умножения (продолжение)
-
Пусть есть какие-то числа a1, a2,
a3, например, a1=3,
a2=2, a3=4.
+, -, *, / - это знаки операторов, то есть знаки, которые предписывают определенные действия. Всякое действие характеризуется направлением; в общем случае идут от чего-то к чему-то и в результате получают что-то. Будем считать, что действия выполняются слева направо. Тогда запись вида a + b предписывает нам взять объект а и осуществить операцию сложения с объектом b. То есть она предписывает порядок осуществления операции. Будем считать, что операция сложения двух множеств заключается в непрерывном пересчете элементов одного множества и затем второго множества. Например, если мощность mA множества А =3, mB множества В равна 2, то сложение заключается в том, что мы пересчитываем элементы множества А: 1,2,3 и затем продолжаем непрерывный счет, перейдя к пересчёту элементов множества В: 4, 5. Т.о. оказывается, что последнее число, полученное в результате пересчёта, представляет сумму чисел, результат сложения равен 5. Если мы начнём пересчет с элементов множества В: 2+3, то получим тот же результат. В этом заключается закон коммутативности: применение операции сложения к объектам не зависит от их порядка: a+b=b+a
Значительный интерес представляет собой операция вычитания, определенная как противоположная операции сложения, но определенная независимо от неё. Под операцией вычитания следует понимать обратный счёт, именно, если даны два множества А и В, то А-В определяется как обратный счет элементов А на величину мощности множества элементов В Например, если mA = 3, mВ = 5, то обратный пересчёт даёт: 3,2,1,-1,-2. Т.о. в результате вычитания мы получили новое множество с отрицательными элементами. Если же мы будем рассматривать разность В - А, то получим 2. Т.о., при вычитании имеет значение порядок объектов при применении операции, а-b≠b-a; тем не менее, результаты оказываются сопряженными друг с другом, то есть а-b=-(b-a). Очевидно, что свойство сопряженности получаемых результатов при коммутации элементов разности даёт нам ту же сопряженность, которую впоследствии встречаем при нахождении корней из положительных чисел.
Закон ассоциативности выполняется для операции сложения на основании очевидных соображений, закон ассоциативности для вычитания не выполняется. Например, 2-(3-4)=3, (2-3)-4 = -5
Законы коммутативности и дистрибутивности для умножения непосредственно иллюстрируются деревьями рис.1. Закон ассоциативности иллюстрируется рис.2:
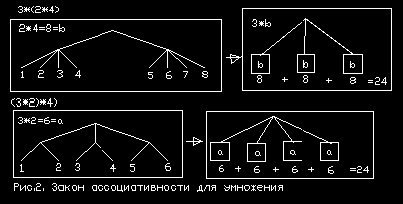 пусть a1, a2,
a3 равны соответственно 3,2,4, тогда a1*
a2*a3
=3*2*4.
Закон ассоциативности гласит, что порядок
выполнения операторов умножения (как и сложения) не имеет значения: a1*(
a2* a3)
= (a1* a2)*
a3
пусть a1, a2,
a3 равны соответственно 3,2,4, тогда a1*
a2*a3
=3*2*4.
Закон ассоциативности гласит, что порядок
выполнения операторов умножения (как и сложения) не имеет значения: a1*(
a2* a3)
= (a1* a2)*
a3
В связи с этим отметим, что закон коммутативности говорит, что не имеет значение порядок объектов при выполнении операций сложения и умножения, закон ассоциативности - что не имеет значения порядок выполнения операторов.
Возведение в степень: 23=2*2*2=2+2+2+2. С формальной точки зрения возведение в степень легко приводится к операции сначала умножения, а затем сложения. Однако в самой форме выражения степени видно, что в основании мы имеем дело с одним и тем же множеством, а показатель степени указывает на число сомножителей. То есть сравнительно с умножением мы имеем дополнительное ограничение, заключающееся в том, что при переходе к умножению в качестве сомножителей мы имеем множество копий одного и того же множества элементов.
- Знаки
- умножение плюса на плюс или
минуса на минус даёт плюс, умножение минуса на плюс или плюса на
минус даёт минус. Возникает справедливый вопрос: почему так?
Отвечают: так договорились. А почему договорились именно т.о.?
Что мы замечаем в схеме договора? симметрию: одинаковые знаки чисел дают плюс, разные - минус. Что явилось следствием договора? невозможность извлечения корня из отрицательных чисел. Но если существует такая потребность - извлекать корни из отрицательных числе, то за ней должно стоять отношение симметрии операций возведения в степень числа и извлечения из него корня, вообще - прямой и обратной операций.
Прежде, чем продолжить, я выскажу одну идею, которую не буду никак обосновывать, но попрошу вас обратить внимание статью "Числа как операторы" профессора В.А.Брусина. Важным представляется динамический аспект, закладываемый им в понятие числа. Брусин пишет:"
Вернемся к интерпретации чисел как операторов умножения и перенесем ее на комплексные числа.
Каждое комплексное число c будем понимать как оператор, преобразующий радиус-вектор произвольного числа z в радиус-вектор числа cz: z cz. Такое преобразование, исходя из изложенного выше, будет изображаться на комплексной плоскости как некоторая комбинация преобразований растяжения, сжатия, инверсии и поворота. При этом мнимая единица i будет соответствовать оператору поворота радиус-векторов на угол p /2 против часовой стрелки. Это характеристическое свойство можно взять за определение числа i. Это будет определение, из которого исключен всякий мистический смысл. Именно это характеристическое свойство и определяет прикладное значение числа i и комплексных чисел вообще в физике и инженерных науках. "
В связи с идеей рассмотрения чисел как радиус-вектора, можно принять следующие правила относительно знаков:
1. Употребление чисел таково, что числа могут рассматриваться как положительные, отрицательные и не имеющие знака. Последний способ употребления чисел появляется, начиная с операции умножения так, как об этом говорилось выше.
2.При рассмотрении чисел важным является направление вращения представляющего их радиус-вектора как положительного либо отрицательного. Тогда знак результата умножения -а*b и a*(-b), то есть минуса на плюс либо плюса на минус будет определяться направлением вращения радиус-вектора.
3. произведение минуса на минус всегда даёт минус, произведение плюса на плюс всегда даёт плюс.
Рассмотрим содержательные аспекты употребления знаков, которое, как видно, связано с вопросом симметрии прямых и обратных операций.
Возьмём декартову систему координат на плоскости. По осям абсцисс и ординат мы имеем дело с числами. Возьмём произведение чисел xi*yj, где 0<i,j<∞ В результате мы получим площадь в первом квадранте в качестве положительной, что справедливо. Возьмём произведение произвольных чисел в третьем квадранте. В результате мы также получим площадь. Но площадь эта лежит целиком в отрицательной области, поэтому она не может быть положительной. Она - отрицательная. Поэтому минус на минус никак не может давать плюс.
Теперь возьмём второй и четвёртый квадранты. Они характеризуются числами с противоположными знаками, в связи с чем возникает вопрос о том, какого рода знак будет носить площадь. Если исходить из статического отношения, то мы не сможем сделать никакого утверждения. Речь должна идти о динамике, о процессе, а именно, об изменении, о направлении приращения чисел. Множество возможных площадей и, соответственно, приращений к ним определяется основанием и аргументом радиус-вектора, причем, очевидно, что соотношение чисел хi, yj обусловливается положением аргумента радиус-вектора, а направление процесса и, соответственно, доминирующей составляющей определяется направлением движения радиус- вектора точки, представляющей пару чисел. Поэтому здесь должно присутствовать "над" и "под", во-первых, направление процесса, которым показывается доминирующая тенденция, и во вторых, "мера силы" "обороняющейся" стороны. Если формально принять равновесие противоположных сторон как равенство чисел, дающее в качестве площади квадрат, то все остальные площади при постоянном модуле должны рассматриваться по тому, происходит ли приближение к квадрату либо удаление от него. Если приближение к квадрату, то доминирует сторона, имеющая большее число, и, соответственно, площадь имеет знак большего числа, однако, так как движение отрицательное, то само это доминирование является ложным, умирающим. Напротив, если удаление от квадрата, то доминирование является истинным. Соответственно получаем: при движении против часовой стрелки радиус - вектора во втором квадранте мы получаем минус, в третьем квадранте - плюс, если движение радиус вектора по часовой стрелке, то во втором квадранте получаем плюс, в третьем - минус.
Сказанное позволяет определить мнимое число i как равное -1, умножение -1*-1 даёт -1, соответственно, корень из -1 даёт -1. Т.о. мы получаем две качественно противоположные единицы - положительную и отрицательную, то есть своего рода распадение беззнаковой единицы на свои противоположные стороны.
Еще одно замечание по поводу закона знаков. В качестве исходного мы имеем при умножении тиражируемое множество, элементы которого могут быть положительными либо отрицательными. В то же самое время множители-тиражиторы не могут быть ни положительными, ни отрицательными, поскольку ими утверждается лишь количество копий исходного множества, "число раз". Поэтому в результате мы получаем те качественные элементы, которые принадлежат тиражируемому множеству. Поэтому в результате мы получаем либо элемент отрицательные, либо положительные. Например, -3*2 = (-1+-1+-1)+(-1+-1+-1)=-6. В то же самое время выражение вида -3*-3 не принадлежит линейному принципу и должно рассматриваться в другой системе понятий
18.07.08 г.