Определения
- Количество материи (масса) есть мера таковой, устанавливаемая пропорционально плотности и объему ее.
Воздуха двойной плотности в двойном объеме вчетверо больше, в тройном — вшестеро. То же относится к снегу или порошкам, когда они уплотняются от сжатия или таяния. Это же относится и ко всякого рода телам, которые, в силу каких бы то ни было причин, уплотняются. Однако при этом я не принимаю в расчет той среды, если таковая существует, которая свободно проникает в промежутки между частицами. Это же количество я подразумеваю в дальнейшем под названиями тело или масса. Определяется масса по весу тела, ибо она пропорциональна весу, что мною найдено опытами над маятниками, произведенными точнейшим образом, как о том сказано ниже.5
5 Ни одно определение Ньютона не вызывало столько критических замечание и столько толкований, как это первое, высказанное такими словаки: «quantitas materiae est mensura ejusdem orta ex iliius densitate et magnitudine conjunctim». В пояснении к этому определению указывается, что слова «quantitas materiae» — «количество материи» равносильны слонам «corpus» — «тело» или «massa». Таким образом в этом определении слова «количество материи» составляют как бы одно слово, один новый термин, который при дальнейшем развитии науки не удержался, и в современной терминологии заменен равносильным ему термином «масса». Словам «количество материи» теперь придается несколько иной смысл, нежели им придавал Ньютон в своем определении. То, что теперь разумеется под словами «количество материи», он просто выражает словом «материи», заменив его местоимением „ejusdem" — „таковой". Поэтому он и в пояснении не говорит «количество воздуха двойной плотности в двойном объеме вчетверо больше», а просто «воздуха».
Необходимо также иметь в виду, что в то время при установлении меры для какой-либо величины устанавливалась лишь ее пропорциональность другим величинам, от коих эта мера зависит. Тогда не говорили, как теперь (когда делается определенное предположение о принятой единице меры), «площадь прямоугольника равняется произведению из его основания на высоту», а говорили (предполагая единицу меры произвольной) «площадь прямоугольника пропорциональна его основанию и высоте».
До Ньютона понятие о массе не вводилось, и рассматривался лишь вес — pondus тела, и при старинной терминологии понятно, что плотность не определялась как касса единицы объема вещества, а говорилось, что плотность тела пропорциональна его весу и обратно пропорциональна его объему.
Имея это в виду, можно ньютоново определение, придерживаясь теперешней терминологии, выразить так: «масса есть мера количества вещества, пропорциональная его плотности и объему». Самым существенным в ньютоновом пояснении вводимого им термина и понятия масса есть установление опытным путем пропорциональности между массою тела и его весом. - Количество движения есть мера такового, устанавливаемая пропорционально скорости и массе.
Количество движения целого есть сумма количеств движения отдельных частей его, значит для массы, вдвое большей, при равных скоростях оно двойное, при двойной же скорости — четверное. б
6 Второе определение выражено следующими словами: «quantitas motus est mensura ejusdem orta ex velocitate et quantitate materiae conjunctim», т. е. оно выражено совершенно подобно первому, и им вводится новый термин «количество движения», сохранившийся и доселе. Слова «orta conjunctim» указывают на совместную пропорциональность той величины, которая названа «количество движения» и которая могла бы быть названа и каким-либо одним словом, как, напр., у англичан, словом «momentum», почему, придерживаясь современное терминологии, они им переведены словами «устанавливаемая пропорционально массе и скорости».
Необходимо иметь в виду, что высказывая это определение, Ньютон придает слову «motus» — „движение" не смысл названия общеизвестного явления, а вводит некоторую новую величину, имеющую при рассмотрении этого явления первенствующее значение. Это особенно ясно выступает в первых словах пояснения: «motus totius est summa motuum in partibus singulis, т. е., переводя буквально, «движение целого есть сумма движений в отдельных частях». Из этих слов ясно, что под словом «motus» он разумеет нечто измеримое, как бы заключающееся или содержащееся в движущемся теле. Вот почему эти слова и переведены так: «Количество движения целого есть сумма количеств движения отдельных частей его», так как теперь слову «движение» иного смысла, как название самого явления, не придается.
- Врожденная сила материи есть присущая ей способность сопротивления, по которой всякое отдельно взятое тело, поскольку оно предоставлено самому себе, удерживает7 свое состояние покоя или равномерною прямолинейного движения.
Эта сила всегда пропорциональна массе, и если отличается от инерции массы, 8 то разве только воззрением на нее.
От инерции материи происходит, что всякое тело лишь с трудом выводится из своего покоя или движения. Поэтому «врожденная сила» могла бы быть весьма вразумительно названа «силою инерции». Эта сила проявляется телом единственно лишь, когда другая сила, к нему приложенная, производит изменение в его состоянии. Проявление этой силы может быть рассматриваемо двояко: и как сопротивление и как напор. Как сопротивление — поскольку тело противится действующей на него силе, стремясь сохранить свое состояние; как напор — поскольку то же тело, с трудом уступая силе сопротивляющееся ему препятствия, стремится изменить состояние этого препятствия. Сопротивление приписывается обыкновенно телам покоящимся, напор — телам движущимся. Но движение и покой, при обычном их рассмотрении, различаются лишь в отношении одного к другому, ибо не всегда находится в покое то, что таковым простому взгляду представляется.
Как в этом определении, так и при формулировке первого закона движения, Ньютон пользуется глаголом «perseverare», включающем в себе не только понятие о сохранении чего-либо, но еще и понятия о длительности и упорстве такого сохранения, поэтому слова «persevеrare in statu quo» наиболее точно передаются словами: «продолжает упорно пребывать в своем состоянии»; слова «удерживает свое состояние» передают короче те же понятия, хотя и с меньшею силою выражения. Вообще латынь Ньютона отличается силою выражений: так, тут сказано «реrsеvеrаrе» — «упорно пребывать», а не «manerе» — «пребывать или оставаться»; когда говорится, что какое-либо тело действием силы отклоняется от прямолинейного пути, то употребляется не просто слово «deviatur» — «отклоняется», a «retrahitur» — «оттягивается»; про силу не говорится просто, что она прикладывается, «applicatur», к телу, a «imprimitur», т. е. «вдавливается» или «втискивается» в тело и т. п. В переводе принята менее выразительная, но общеупотребительная теперь терминология. - Приложенная сила есть действие, производимое над телом, чтобы изменить его состояние покоя или равномерного прямолинейного движения.
Сила проявляется единственно только в действии, и по прекращении действия в теле не остается. Тело продолжает затем удерживать свое новое состояние вследствие одной только инерции. Происхождение приложенной силы может быть различное: от удара, от давления, от центростремительной силы. - Центростремительная сила есть та, с которою тела к некоторой точке, как к центру, отовсюду притягиваются, гонятся или как бы то ни было стремятся.
Такова сила тяжести, под действием которой тела стремятся к центру Земли; магнитная сила, которою железо притягивается к магниту, и та сила, каковою бы она ни была, которою планеты постоянно отклоняются от прямолинейного движения и вынуждаются обращаться по кривым линиям. Камень, вращаемый в праще, стремится удалиться от вращающей пращу руки, и этим своим стремлением натягивает пращу тем сильнее, чем быстрее вращение, и как только ее пустят, то камень улетает.
Силу, противоположную сказанному стремлению, которою праща постоянно оттягивает камень к руке и удерживает его на круге, т. е. силу, направленную к руке или к центру описываемого круга, я и называю центростремительной. Это относится и до всякого тела, движущегося по кругу. Все такие тела стремятся удалиться от центра орбиты, и если бы не было некоторой силы, противоположной этому стремлению, которая их и удерживает на их орбитах, то они и ушли бы по прямым линиям, двигаясь равномерно. Эту то силу я и называю центростремительной. Брошенное тело, если бы силы тяжести не было, не отклонялось бы к Земле, а уходило бы в небесное пространство по прямой линии равномерно, если бы не было и сопротивления воздуха. Своею тяжестью оно оттягивается от прямолинейного пути и постоянно отклоняется к Земле в большей или меньшей степени, сообразно напряжению силы тяжести и скорости движения. Чем меньше будет отнесенное к массе напряжение тяжести и чем больше будет скорость, с которою тело брошено, тем менее оно отклонится от прямой линии и тем дальше отлетит.
Если свинцовое ядро, брошенное горизонтально силою пороха из пушки, поставленной на вершине горы, отлетит по кривой, ранее чем упасть на землю, на две мили, то предполагая, что сопротивления воздуха нет, если его бросить с двойною скоростью, оно отлетит приблизительно вдвое дальше, если с десятерною, то — в десять раз. Увеличивая скорость, можно по желанию увеличить и дальность полета и уменьшать кривизну линии, по которой ядро движется, так что можно бы заставить его упасть в расстоянии и десяти градусов, и тридцати, и девяноста, можно бы заставить его окружить всю Землю или даже уйти в небесные пространства и продолжать удаляться до бесконечности. Подобно тому как брошенное тело может быть отклонено силою тяжести так, чтобы описывать орбиту вокруг Земли, так и Луна или силою тяжести, если она ей подвержена, или же иною силою, которая влечет ее к Земле, может быть отклоняема от прямолинейного пути и вынуждена обращаться по своей орбите; без такой силы Луна не могла бы удерживаться на своей орбите. Если бы эта сила была меньше соответствующей этой орбите, то она отклоняла бы Луну от прямолинейного пути недостаточно, а если больше, то отклонила бы ее более, чем следует, и приблизила бы ее от орбиты к Земле. Следовательно, надо, чтобы эта сила была в точности надлежащей величины. Дело математиков найти такую силу, которая в точности удерживала бы заданное тело в движении по заданной орбите с данною скоростью, и наоборот, найти тот криволинейный путь, на который заданною силою будет отклонено тело, вышедшее из заданного места с заданною скоростью.
В центростремительной силе различается три рода величин: абсолютная, ускорительная и движущая. - Абсолютная величина центростремительной силы
есть мера большей или меньшей мощности самого источника ее распространения из центра в окружающее его пространство
Так, магнитная сила, в зависимости от величины магнита или степени намагничивания, может быть в одном магните больше, в другом меньше. - Ускорительная9 величина центростремительной силы есть мера, пропорциональная той скорости, которую она производит в течение данного времени.
Так, действие того же магнита более сильно на близком расстоянии, слабее — на дальнем, или сила тяжести больше в долинах, слабее на вершинах высоких гор и еще меньше (как впоследствии будет показано) на еще бо'льших расстояниях от земного шара; в равных же расстояниях она везде одна и та же, ибо, при отсутствии сопротивления воздуха, все падающие тела (большие или малые, тяжелые или легкие) ускоряются ею одинаково.
9 Вся первая книга «Начал» занята почти исключительно учением о центростремительных силах и их действиях. При этом всегда Ньютон рассматривает лишь «ускорительную силу» в данном месте. При теперешней терминологии можно сказать, что в первой книге им исследуются «силы поля», и то, что он называет «ускорительная сила», теперь называется «напряжение поля» в данном месте. Замечательно, что Ньютон, вводя понятие «ускорительная сила», не пользуется понятием об ускорении, а заменяет его скоростью, производимою в продолжение заданного времени. Вообще понятие ускорения, как оно разумеется теперь, в «Началах» не применяется, и под словом «acceleratio»—«ускорение» всегда разумеется приращение скорости в течение заданного конечного или бесконечно малого промежутка времени. - Движущая величина центростремительной силы есть ее мера, пропорциональная количеству движения, которое ею производится в течение данною времени.
Таким образом вес большей массы больше, меньшей — меньше; для той же самой массы или того же самого тела вес больше вблизи Земли, меньше в небесной дали. Эта величина есть направленное к центру стремление всего тела, которое и называется его весом. Движущая сила распознается по силе, ей равной и противоположной, которая могла бы воспрепятствовать опусканию тела. 10
Для краткости эти величины сил можно называть силами движущими, ускоряющими и абсолютными, и для отличия — относить их к самим притягиваемым к центру телам, к месту тел и к центру сил, а именно: движущую силу — к телу, как стремление всего тела к центру, причем это полное стремление составляется из стремлений отдельных частиц тела; силу ускорительную — к месту тела в пространстве, как некоторую способность, распространенную центром на все места окружающего пространства и заставляющую приходить в движение тела, в этих местах находящиеся, абсолютную же силу — к самому центру, как заключающуюся в нем причину, без которой движущие силы не распространялись бы в окружающем пространстве; сказанною причиною может служить или какое-либо центральное тело (как, напр., магнит в центре сил магнитных или Земля в центре сил тяжести), или что бы то ни было иное, хотя бы и ни чем не обнаружимое. Эти понятия должно рассматривать как математические, ибо я еще не обсуждаю физических причин и места нахождения сил. Таким образом ускорительная сила так относится к движущей, как скорость к количеству движения. В самом деле, количество движения пропорционально скорости и массе, движущая же сила пропорциональна ускорительной и массе, ибо сумма11 действий ускорительной силы на отдельные частицы тела и составляет движущую силу его. Поэтому близ поверхности Земли, где ускоряющая сила тяжести для всех тел одна и та же, движущая сила тяжести, или вес, пропорциональна массе тела. Если подняться в такие области, где ускоряющая12 сила тяжести будет меньше, то и вес пропорционально уменьшится; вообще вес будет постоянно пропорционален массе тела и ускоряющей силе тяжести. Так, напр., в тех областях пространства, где ускоряющая сила тяжести вдвое меньше, вес массы вдвое или втрое меньшей будет вчетверо или вшестеро меньше, нежели близ поверхности Земли. 13 Далее я придаю тот же самый смысл названиям «ускорительные и движущие притяжения и натиски».14 Название же «притяжение» (центром), «натиск» или «стремление» (к центру) я употребляю безразлично одно вместо другого, рассматривая эти силы не физически, а математически, поэтому читатель должен озаботиться, чтобы, в виду таких названий, не думать, что я ими хочу определить самый характер действия или физические причины происхождения этих сил, или же приписывать центрам (которые суть мате¬матические точки) действительно и физически силы, хотя я и буду говорить о силах центров и о притяжении центрами.
10 Давая определение понятия «движущая сила», т. е. того, что теперь зовут просто «сила», Ньютон обращает внимание на способ ее измерения и именно — способ статический, уравновешивая другою силою, препятствующей движению к центру. В этих немногих словах и установлена связь между статикою и динамикою при посредстве второго закона — сила статически вдвое большая сообщает и вдвое бо'льшее количество движения в заданное время. Замечательно также, что нигде Ньютон не говорит, чтобы сила измерялась произведением из массы на ускорение, но что движущая сила пропорциональна произведению из ускоряющей и массы, и ускоряющая сила не есть понятие, равнозначащее ускорению, а, как уже сказано, напряжению поля в данном месте, т. е. это есть сила, действующая на массу, равную единице. Ньютон, если и не применял, то ясно представлял измерение силы при помощи растяжения пружины или нити, вообще динамометра; это можно видеть из его поучения в конце этой главы, где он указывает, как различить абсолютное движение от относительного, и, приводя опыт с шарами, говорит: «по натяжению нити (соединяющей шары), можно будет узнать их стремление удалиться от оси вращения и по нему вычислить количество движения», т. е. он здесь имеет в виду именно такое «статическое» измерение силы, и по нему находит ее действие.
11 Отсюда следует, что масса всего тела считается равной сумме масс частиц его.
12 Ньютон употребляет термины «gravitas acceleratrix» и «gravitas motrix», т. е. „ускоряющая тяжесть" и „движущая тяжесть". Современные термины: «напряжение силы тя¬жести» и «сила тяжести или вес».
13 В этих словах и устанавливается различие веса и массы при пропорциональности их между собою.
14 Точный смысл латинского слова «impulsus» вполне передается словом «натиск», включающим в себя как понятие о напряженности, так и продолжительности действия.
-
ПОУЧЕНИЕ
В изложенном выше имелось в виду объяснить, в каком смысле употребляются в дальнейшем менее известные названия. Время, пространство, место и движение составляют понятия общеизвестные. Однако необходимо заметить, что эти понятия обыкновенно относятся к тому, что постигается нашими чувствами. Отсюда происходят некоторые неправильные суждения, для устранения которых необходимо вышеприведенные понятия разделить на абсолютные и относительные, истинные и кажущиеся, математические и обыденные.
I. Абсолютное, истинное математическое время само по себе и по самой своей сущности, без всякого отношения к чему-либо внешнему, протекает равномерно, и иначе называется длительностью.
Относительное, кажущееся или обыденное время есть или точная, или изменчивая, постигаемая чувствами, внешняя, совершаемая при посредстве какого-либо движения, мера продолжительности, употребляемая в обыденной жизни вместо истинного математического времени, как то: час, день, месяц, год.
II. Абсолютное пространство по самой своей сущности, безотносительно к чему бы то ни было внешнему, остается всегда одинаковым и неподвижным.
Относительное есть его мера или какая-либо ограниченная подвижная часть, которая определяется нашими чувствами по положению его относительно некоторых тел и которое в обыденной жизни принимается за пространство неподвижное: так, напр., протяжение пространств подземного воздуха или надземного, определяемых по их положению относительно Земли. По виду и величине абcолютное и относительные пространства одинаковы, но численно не всегда остаются одинаковыми. Так, напр., если рассматривать Землю подвижною, то пространство нашего воздуха, которое по отношению к Земле остается всегда одним и тем же, будет составлять то одну часть пространства абсолютного, то другую, смотря по тому, куда воздух перешел, и следовательно, абсолютно сказанное пространство беспрерывно меняется.
III. Место есть часть пространства, занимаемая телом, и по отношению к пространству бывает или абсолютным или относительным. Я говорю «часть пространства», а не положение тела и не объемлющая его поверхность. Для равнообьемных тел места равны, поверхности же от несходства формы тел могут быть и неравными. Положение, правильно выражаясь, не имеет величины, и оно само по себе не есть место, а принадлежащее месту свойство. Движение целого то же самое, что совокупность движений частей его, т. е. перемещение целого из его места то же самое, что совокупность перемещений его частей из их мест; поэтому место целого то же самое, что совокупность мест его частей, и следовательно, оно целиком внутри всего тела.
IV. Абсолютное движение есть перемещение тела из одного абсолютного его места в другое, относительное — из относительного в относительное же. Так, на корабле, идущем под парусами, относительное место тела есть та часть корабля, в которой тело находится, напр. та часть трюма, которая заполнена телом и которая, следовательно, движется вместе с кораблем. Относительный покой есть пребывание тела в той же самой области корабля или в той же самой части его трюма.
Истинный покой есть пребывание тела в той же самой части того неподвижного пространства, в котором движется корабль со всем в нем находящимся. Таким образом, если бы Земля на самом деле покоилась, то тело, которое по отношению к кораблю находится в покое, двигалось бы в действительности с тою абсолютною скоростью, с которою корабль идет относительно Земли. Если же и сама Земля движется, то истинное абсолютное движение тела найдется по истинному движению Земли в неподвижном пространстве и по относительным движениям корабля по отношению к Земле и тела по кораблю.
Так, если та часть Земли, где корабль находится, движется на самом деле к востоку со скоростью 10 010 частей, корабль же идет к западу со скоростью 10 частей, моряк же ходит по кораблю и идет к востоку со скоростью одной части, то истинно и абсолютно моряк перемещается в неподвижном пространстве к востоку со скоростью 10 001 частей, по отношению же к Земле — на запад со скоростью 9 частей.
Абсолютное время различается в астрономии от обыденнного солнечного времени уравнением времени. Ибо естественные солнечные сутки, принимаемые при обыденном измерении времени за равные, на самом деле между собою неравны. Это неравенство и исправляется астрономами, чтобы при измерениях движений небесных светил применять более правильное время. Возможно, что не существует (в природе) такого равномерного движения, которым время могло бы измеряться с совершенною точностью. Все движения могут ускоряться или замедляться, течение же абсолютного времени изменяться не может. Длительность или продолжительность существования вещей одна и та же, быстры ли движения (по которым измеряется время), медленны ли, или их совсем нет, поэтому она надлежащим образом и отличается от своей, доступной чувствам, меры, будучи из нее выводимой при помощи астрономического уравнения. Необходимость этого уравнения обнаруживается как опытами с часами, снабженными маятниками, так и по затмениям спутников Юпитера.
Как неизменен порядок частей времени, так неизменен и порядок частей пространства. Если бы они переместились из мест своих, то они продвинулись бы (так сказать) в самих себя, ибо время и пространство составляют как бы вместилища самих себя и всего существующего. Во времени все располагается в смысле порядка последовательности, в пространстве — в смысле порядка положения. По самой своей сущности они суть места, приписывать же первичным местам движения нелепо. Вот эти-то места и суть места абсолютные, и только перемещения из этих мест составляют абсолютные движения.
Однако совершенно невозможно ни видеть, ни как-нибудь иначе различить при помощи наших чувств отдельные части этого пространства одну от другой, и вместо них приходится обращаться к измерениям, доступным чувствам. По положениям и расстояниям предметов от какого-либо тела, принимаемого за неподвижное, определяем места вообще, затем и о всех движениях судим по отношению к этим местам, рассматривая тела лишь как переносящиеся по ним. Таким образом вместо абсолютных мест и движений пользуются относительными; в делах житейских это не представляет неудобства, в философских необходимо отвлечение от чувств. Может оказаться, что в действительности не существует покоящегося тела, к которому можно было бы относить места и движения прочих.
Абсолютное и относительное движение и абсолютный и относительный покой отличаются друг от друга: свойствами, причинами происхождения и проявлениями.
Свойство покоя состоит в том, что тела истинно покоящиеся находятся в покое и друг относительно друга. Возможно, что какое-нибудь тело в области неподвижных звезд, а может быть, и много далее, находится в абсолютном покое, но узнать по взаимному положению тел в наших областях, не сохраняет ли какое-нибудь из них постоянное положение относительно этого весьма отдаленного нельзя. Невозможно также определить истинный их покой по относительному их друг к другу положению.
Свойство движения состоит в том, что части, сохраняющие постоянное положение по отношению к целому, участвуют в движении этого целого. Так, все части вращающихся тел стремятся удалиться, от оси вращения, для движущихся поступательно полное движение образуется из соединения отдельных частных движений. Следовательно, когда движутся окружающие тела, то движутся и те, которые по отношению к ним находятся в покое; поэтому нельзя определить истинное абсолютное движение по перемещениям от соседних тел, рассматриваемых как неподвижные. Эти тела должны быть действительно в покое, а не только приниматься за покоящиеся. В противном случае все содержащиеся тела участвовали бы в истинных движениях тел, их окружающих, и если бы это последнее движение прекратить, то они оказались бы на самом деле не в покое, а лишь представлялись до тех пор находящимися в таковом. Окружающие тела по отношению к содержащимся стоят в том же отношении, как наружная часть целого к его внутренней части или как скорлупа к ядру. При движении скорлупы движется и ядро, не перемещаясь относительно скорлупы, т. е. движется как часть целого.
В тесной связи с предыдущим свойством находится такое: тело, движущееся в подвижном пространстве, участвует и в движении этого пространства, поэтому тело, движущееся от подвижного места, участвует в движении своего места. Следовательно, все движения, совершающиеся от подвижных мест, суть лишь составляющие части полных абсолютных движений, и всякое полное движение составляется из движения тела от первого места своего, из движения этого первого от его места и так далее, пока не достигнем до места неподвижного, как это было пояснено примером моряка, приведенным выше. Таким образом полные абсолютные движения могут быть определены не иначе, как при помощи мест неподвижных, почему я и относил их выше к местам неподвижным, относительные же движения — к местам подвижным. Места же неподвижны не иначе, как если они из вечности в вечность сохраняют постоянные взаимные положения и, следовательно, остаются всегда неподвижными и образуют то, что я называю неподвижным пространством.
Причины происхождения, которыми различаются истинные и кажущиеся движения, суть те силы, которые надо к телам приложить, чтобы произвести эти движения. Истинное абсолютное движение не может ни произойти, ни измениться иначе, как от действия сил, приложенных непосредственно к самому движущемуся телу, тогда как относительное движение тела может быть и произведено и изменено без приложения сил к этому телу; достаточно, чтобы силы были приложены к тем телам, по отношению к которым это движение определяется. Когда эти тела будут уступать действию сил, то будет изменяться и то относительное положение, которым определяется относительный покой или относительное движение. Наоборот, истинное движение всегда изменяется от приложения к телу сил, относительное же движение может при таком приложении сил и не изменяться. Так, напр., если и к тем телам, к которым движение заданного тела относится, будут приложены такие силы, что относительное положение всех тел будет сохраняться, то сохранится и относительное движение заданного тела по отношению к прочим. 15 Таким образом всякое относительное движение может быть изменяемо такими действиями, при которых абсолютное движение не меняется, и может сохраняться при таких, от которых абсолютное изменяется, так что абсолютное движение совершенно не зависит от тех соотношений, которыми определяется движение относительное.
Проявления, которыми различаются абсолютное и относительное движение, состоят в силах стремления удалиться от оси вращательного движения, ибо в чисто относительном вращательном движении эти силы равны нулю, в истинном же и абсолютном они больше или меньше, сообразно количеству движения. Если на длинной веревке подвесить сосуд и, вращая его, закрутить веревку, пока она не станет совсем жесткой, затем наполнить сосуд водой и, удержав сперва вместе с водою в покое, внезапным действием другой силы привести сосуд во вращение в сторону раскручивания веревки, то сосуд будет продолжать вращаться, причем это вращение будет поддерживаться достаточно долго раскручиванием веревки. Сперва поверхность воды будет оставаться плоской, как было до движения сосуда. Затем сосуд силою, постепенно действующею на воду, заставит и ее участвовать в своем вращении. По мере возрастания вращения вода будет постепенно отступать от середины сосуда и возвышаться по краям его, принимая впалую форму поверхности (я сам это пробовал делать); при
_________________
15 Это свойство относительного движения высказано еще вторично, как следствие VI законов движения.
усиливающемся движении она все более и более будет подниматься к краям, пока не станет обращаться в одинаковое время с сосудом и придет по отношению к сосуду в относительный покой. Этот подъем воды указывает на стремление ее частиц удалиться от оси вращения, и по этому стремлению обнаруживается и измеряется истинное и абсолютное вращательное движение воды, которое, как видно, во всем совершенно противоположно относительному движению. В начале, когда относительное движение воды в сосуде было наибольшее, оно совершенно не вызывало стремления удалиться от оси — вода не стремилась к окружности и не повышалась у стенок сосуда, а ее поверхность оставалась плоской и истинное вращательное ее движение еще не начиналось. Затем, когда относительное движение уменьшилось, повышение воды у стенок сосуда обнаруживало ее стремление удалиться от оси и это стремление показывало постепенно возрастающее истинное вращательное движение воды, и когда оно стало наибольшим, то вода установилась в покое относительно сосуда. Таким образом это стремление не зависит от движения воды относительно окружающего тела, следовательно по таким движениям нельзя определить истинно вращательное движение тела. Истинное круговое движение какого-либо тела может быть лишь одно в полном соответствии с силою стремления его от оси, относительных же движений, в зависимости от того, к чему они относятся, тело может иметь бесчисленное множество; но, независимо от этих отношений, эти движения совершенно не сопровождаются истинными проявлениями, если только это тело не обладает, кроме этих относительных, и сказанным единственным истинным движением. Поэтому в тех системах мира, в которых предполагается, что наши небесные сферы обращаются внутри сферы неподвижных звезд и несут с собою планеты, окажется, что отдельные части этих сфер и планеты, покоящиеся относительно своих сфер, на самом деле движутся, ибо они меняют относительное положение (чего не может быть для тел, покоящихся абсолютно); вместе с тем они участвуют в общем движении несущих их сфер и, значит, как части вращающегося целого, стремятся отдалиться от оси.
Таким образом относительные количества не суть те самые количества, коих имена им обычно придаются, а суть лишь результаты измерений сказанных количеств (истинные или ложные), постигаемые чувствами и принимаемые обычно за самые количества. Если значение слов определять по тому смыслу, в каком эти слова обычно употребляются, то под названиями «время», «пространство», «место» и «движение» и следует разуметь эти постижимые чувствами меры их.
Речь стала бы совершенно необычной и чисто математической, если бы под этими названиями разуметь действительно сами измеряемые количества. Поэтому воистину насилуют смысл священного писания те, кто эти слова истолковывают в нем как самые количества. Не менее того засоряют математику и физику и те, кто смешивает самые истинные количества с их отношениями и их обыденными мерами.
Распознание истинных движений отдельных тел и точное их разграничение от кажущихся весьма трудно, ибо части того неподвижного пространства, о котором говорилось и в котором совершаются истинные движения тел, не ощущаются нашими чувствами. Однако это дело не вполне безнадежное. Основания для суждений можно заимствовать частью из кажущихся движений, представляющих разности истинных, частью из сил, представляющих причины и проявления истинных движений. Так, если два шара, соединенные нитью на данном друг от друга расстоянии, будут обращаться около общего их центра тяжести, то по натяжению нити можно будет узнать стремление шаров к удалению от оси вращения и по нему вычислить угловую его скорость. Если затем на противоположные стороны шаров заставить действовать равные силы, так чтобы они или увеличивали, или уменьшали, круговращательное движение, то по увеличившемуся или по уменьшившемуся натяжению нити может быть обнаружено увеличение или уменьшение скорости движения, и таким образом можно будет найти те стороны шаров, к которым надо приложить силы, чтобы увеличение скорости движения стало наибольшим, и значит, найти те стороны шаров, которые обращены по направлению движения или по направлению, ему обратному. Когда эти передние и задние стороны будут найдены, то и движение будет вполне определено.
Таким способом могло бы быть определено количество и направление кругового движения внутри огромного пустого пространства, где не существовало бы никаких внешних доступных чувствам признаков, к которым можно было бы относить положения шаров. Если бы в этом пространстве, кроме того, находились бы еще некоторые весьма удаленные тела, сохраняющие относительные друг к другу положения, подобно тому как наши неподвижные звезды, то по перемещению шаров относительно этих тел мы не могли бы определить, чему принадлежит это перемещение — телам или шарам. Но если бы мы, определив натяжение нити, нашли бы, что это натяжение как раз соответствует движению шаров, то мы бы заключили, что движение принадлежит шарам, а не внешним телам, и что эти тела находятся в покое. Таким образом по видимому перемещению шаров относительно внешних тел мы вывели бы их движение. Нахождение же истинных движений тел по причинам, их производящим, по их проявлениям и по разностям кажущихся движений и, наоборот, нахождение по истинным или кажущимся движениям их причин и проявлений излагаются подробно в последующем. Именно с этою-то целью и составлено предлагаемое сочинение.
АКСИОМЫ ИЛИ ЗАКОНЫ ДВИЖЕНИЯ
- Всякое тело продолжает удерживаться в своем состоянии покоя или равномерного и прямолинейного движения, пока и поскольку оно не понуждается приложенными силами изменять это состояние.16
Брошенное тело продолжает удерживать свое движение, поскольку его не замедляет сопротивление воздуха и поскольку сила тяжести не побуждает это тело вниз. Волчок, коего части, вследствие взаимного сцепления, отвлекают друг друга от прямолинейного движения, не перестает вращаться {равномерно), поскольку это вращение не замедляется сопротивлением воз¬духа. Бо'льшие же массы планет и комет, встречая меньшее сопротивление в свободном пространстве, сохраняют свое как поступательное, так и вращательное движение в продолжение гораздо большего времени.
______________
16 В виду важности основных законов движения приводим и подлинную их формулировку.
Закон I высказан так: «Corpus omne perseverare in statu suo quiescendi vel movendi uniformiter in direсtum, nisi quatenus illud a viribus impressis cogitur statum suum mutare».
Закон II. Mutationem motus proportionalem esse vi motrici impressae et fieri secundum lineam rectam qua visilia imprimitur.
Закон III. Actioni contrariam semper et aequalem esse reactionem: sive corporum duorum actiones in se mutuo semper esse aequales et in partes contrarias dirigi.
Первый закон представляет для точного перевода некоторые затруднения, именно — по отношению к словам «perseverare» и «nisi quateous». Слово «perseverare», как уже упомянуто в примечании 7, включает в себе понятие о стойкости или упорстве в сохранении чего-либо. Но, кроне того, оно может включать и понятие о длительности сохранения или пребывания, и в этом смысле оно или, точнее говоря, соответствующее ему существительное «perseverantia» употреблено Ньютоном в пояснение понятия об абсолютном времени, где сказано прямо: «duratio seu perseverantia existentiae», т. е. «длительность или продолжительность существования» Сообразно тому, какой смысл придать слову «perseverare», надо придавать и смысл словам «nisi quatenus», т. е. «ограничения в смысле времени или в смысле количества», и тогда их надо переводить или слонами: «до тех пор пока» или просто «пока» — в первом случае, и словами: «кроме того поскольку» или просто «поскольку не» — во втором. Таким образом в первом толковании первый закон можно перевести так: «Всякое тело продолжает пребывать в своем состоянии покоя или равномерного и прямолинейного движения, пока приложенные силы не понудят его изменить это состояние». Во втором толковании этот закон можно перевести так: «Всякое тело удерживает свое состояние покоя или равномерного и прямолинейного движения, поскольку оно не понуждается приложенными силами изменять это состояние».
В первом толковании будет оттенено, что одного только времени недостаточно для изменения состояния покоя или равномерного и прямолинейного движения тела, необходимо еще действие силы. Во втором — что тело лишь постольку удерживает свое состояние покоя или равномерного прямолинейного движения, поскольку внешние силы ему в том не препятствуют. В пояснении, в первых двух примерах, как бы оттеняется второе толкование, причем в первом повторено выражение «perseverant nisi quatenus», в третьем же сказано просто «сохраняют» — «conservant», и подчеркнута именно длительность этого сохранения.
Таким образом латинский текст включает в себе одновременно оба толкования или оба понятия, и словом «perseverare» Ньютон использовал всю силу латинского языка. Сочетать совершенно точно в русском переводе оба толкования я не сумел, и в той формулировке, кото¬рая дана в тексте, второе толкование как бы несколько пересиливает.
Как при формулировке, так и при пояснении второго закона, подразумевается, что продолжительность действия силы или постоянная, или одна и та же для сравниваемых сил. В непосредственной связи со вторым законом находится лемма X, в которой показывается, что в пределе для бесконечно малых промежутков времени изменения скорости тела, а значит, и количества движения, производимые силою, пропорциональны времени, пройденное же телом по направлению силы пространство пропорционально квадрату времени. Эта лемма, в связи со вторым законом и с понятием об «ускорении» в его теперешнем смысле, и устанавливает пропорциональность силы ускорению.
В поучении, в конце отдела о законах движения, Ньютон особенно подробно останавливается на третьем законе, показывая как подтверждения его опытами, так и важные его применения во всех случаях, где дело идет не об одном, а о нескольких телах, действующих друг на друга. - Изменение количества движения пропорционально приложенной движущей силе и происходит по направлению той прямой, по которой эта сила действует.
Если какая-нибудь сила производит некоторое количество движения, то двойная сила произведет двойное, тройная — тройное, будут ли они приложены разом все вместе, или же последовательно и постепенно. Это количество движения, которое всегда происходит по тому же направлению, как и производящая его сила, если тело уже находилось в движении, при совпадении направлений прилагается к количеству движения тела, бывшему ранее, при противоположности — вычитается, при наклонности — прилагается наклонно и соединяется с бывшим ранее, сообразно величине и направлению каждого из них. - Действию всегда есть равное и противоположное противодействие, иначе — взаимодействия двух тел друг на друга между собою равны и направлены в противоположные стороны.
Если что-либо давит на что-нибудь другое или тянет его, то оно само этим последним давится или тянется. Если кто нажимает пальцем на камень, то и палец его также нажимается камнем. Если лошадь тащит камень, привязанный к канату, то и, обратно (если можно так выразиться), она с равным усилием оттягивается к камню, ибо натянутый канат своею упругостью производит одинаковое усилие на лошадь в сторону камня и на камень в сторону лошади, и насколько этот канат препятствует движению лошади вперед, настолько же он побуждает движение вперед камня. Если какое-нибудь тело, ударившись в другое тело, изменяет своею силою его количество движения на сколько-нибудь, то оно претерпит от силы второго тела в своем собственном количестве движения то же самое изменение, но обратно направленное, ибо давления этих тел друг на друга постоянно равны. От таких взаимодействий всегда происходят равные изменения не скоростей, а количеств движения, предполагая, конечно, что тела никаким другим усилиям не подвергаются. Изменения скоростей, происходящие также в противоположные стороны, будут обратно пропорциональны массам тел, ибо количества движения получают равные изменения. Этот закон имеет место и для притяжений, как это будет доказано в поучении.
Следствие 1
При силах совокупных тело описывает диагональ параллелограмма в то же самое время, как его стороны — при раздельных.17
Если тело при действии в месте А (фиг. 1)
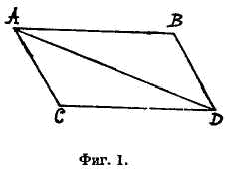одной только силы M перенеслось бы в продолжение заданного промежутка времени равномерным движением из А в В и если бы при действии в том же месте одной только силы N оно перенеслось бы из А в С, то при действии обеих сил оно перенесется в то же самое время из А в D по диагонали параллелограмма ABCD.
Так как сила N действует по направлению прямой АС, параллельной BD, то по второму закону эта сила нисколько не изменит той скорости приближения к прямой BD, которая была произведена первою силою. Следовательно, тело в продолжение данного времени достигнет до линии BD, была ли сила N приложена, или нет. На основании такого же рассуждения, к концу
того же промежутка времени тело должно находиться и где-либо на прямой CD, следовательно оно должно быть в их пересечении D. Переходит же оно из А в D прямолинейно на основании закона I.
_________________________
17 Формулировка этого следствия представляется при теперешнем изложении необычной, и доказательство — как бы ей несоответствующим, ибо в нем предполагается, что когда тело описывает стороны или диагональ параллелограмма, то оно движется равномерно, т. е. силы на него не действуют, а теорема высказана так, что можно думать, что стороны и диагональ параллелограмма описываются при продолжающемся действии сил и притом сил каких угодно, постоянных или переменных, и в продолжение какого угодно, лишь бы во всех случаях того же самого, промежутка времени. Но необходимо иметь в виду второй закон, по которому скорости, сообщаемые разными силами тому же телу, пропорциональны этим силам и так же направлены. В то время, когда были изданы «Начала», представления скорости в виде отрезка прямой не было, почему вместо этого представления Ньютон и берет те пути, которые тело могло бы описать в течение некоторого произвольно заданного промежутка времени, и вот об этом-то времени после прекращения действия силы и идет речь в теореме. Таким образом эта теорема при теперешней терминологии составляет не что иное, как сложение количеств движения по правилу параллелограмма. Первые слова доказательства также весьма кратки; если развить подробно их смысл, то можно бы передать его так; «сила M, действуя одна, могла бы сообщить телу в продолжение некоторого промежутка времени t0 такую скорость, что тело, двигаясь затем из точки А с этою скоростью равномерно, прошло бы в течение данного, промежутка времени Т путь АВ. Сила N, действуя одна, могла бы сообщить в продолжение того же промежутка t0 такую скорость, что тело, двигаясь затем с этою скоростью равномерно, прошло бы в течение данного промежутка времени Т путь АС; тогда если бы на тело действовали одновременно и совместно в течение того же промежутка времени t0 обе силы M и N, то они сообщили бы телу такую скорость, что тело, двигаясь затем с этою скоростью равномерно, прошло бы в течение данного промежутка времени Т путь AD, представляющий диагональ параллелограмма ABCD».
Вторая часть доказательства изложена подробно, и ею вполне разъясняется смысл, который надо придавать как теореме, так и не вполне ясно выраженной первой части доказательства. Можно думать, что потому и теорема и начало ее доказательства и высказаны так неопределенно, чтобы побудить читателя проследить доказательство до конца и самому восполнять краткость формулировки.
Ньютоново доказательство отнюдь не предполагает, что тело до действия сил находилось в покое, в нем также не оговорено, в продолжение какого промежутка времени силы M и N сообщали телу скорости. Этот промежуток времени может быть бесконечно мал, все равносообщенные скорости будут пропорциональны силам, а это значит, что силы M и N могут быть не только постоянные, но и переменные; в этом последнем случае надо предполагать сказанный промежуток бесконечно малым и переходить к пределу. Здесь Ньютон на этом не останавливается, но дальше, в лемме X и в предложении I, он на это обращает внимание.
Следствие II
Отсюда явствует составление силы, направленной по AD, из каких-либо двух наклоненных друг к другу АВ и BD и, наоборот, разложение любой силы, направленной по AD, на наклонные АВ и ВD. Как это сложение, так и разложение беспрестанно подтверждаются в учении о машинах.18
Литература: 1.1
-
[1.1,73]
Из общего рассмотрения движения упругих тел, я заключил, что явления, вызываемые их столкновением, никоим образом не могут доказывать правильность какой-нибудь новой оценки сил, отличной от картезианской, ибо все эти явления выводятся из единственного источника - из произведения массы на скорость, взятого вместе с упругостью.
Стало быть, то, что произведено силой, оцениваемой лишь простой мерой скорости, представляет собой оценку по скорости. В этих выводах сторонников Лейбница, относящихся к столкновению упругих тел, должно где-то содержаться ложное заключение, хотя и в очень скрытом виде. - [1.1,77] ;смысл терминов "мёртвое " и "живое" движение, термина "квадрат"
При сложении мёртвых давлений (мертвое - то, что не движется, живое - движется Ш.), например, тяжестей, действующих из исходной точки под некоторым углом друг к другу, могут быть выражены также линиями, которые составляют стороны прямоугольного параллелограмма, а возникающее отсюда давление изображается диагональю. Хотя и здесь квадрат диагонали равен суме квадратов её сторон, однако отсюда вовсе не следует, что сложная сила будет относиться к какой-нибудь из простых сил как квадрат линий, выражающих первоначальные скорости;
- [3.1,15-16]
Статика
изучает условия равновесия тел, находящихся под действием сил.
Равновесие - состояние покоя тела по отношению к другим телам. Абсолютное равновесие - если движением тела, по отношению к которому изучается равновесие, можно пренебречь. Относительное - в противном случае. Абсолютным можно считать равновесие по отношению к земле.
Тела делятся на твёрдые, жидкие, газообразными. В общей механике рассматриваются твёрдые тела. Твёрдые тела подвержены деформации в зависимости от материала, формы. нагрузок. Абсолютно твёрдое тело - тело, не подверженное деформации (расстояние между любыми двумя его точками постоянно)
Учёт деформаций рассматривается в курсах сопротивления материалов и теории упругости.
Твёрдое тело под действием системы сил находится в равновесии (покое), если удовлетворяет его условиям равновесия,, для определения которых нужно уметь силы складывать, заменять одни системы сил другими, в частности, приводить сложную систему сил к простейшему виду.
Методы решения задач статики - геометрический и графический, в силу наглядности имеющие первостепенную роль, и аналитический. - Сила Состояние равновесия или движения тела зависит от характера его взаимодействий с другими телами в виде давления, притяжения или отталкивания.
Величина, выражающая количественную меру взаимодействия тел называется силой
Величины могут быть скалярными, определяемые их численным значением, и векторными, характеризующие также направление. Сила является векторной величиной. Её действие на тело определяется 1. численной величиной, или модулем; 2. направлением; 3.точкой приложения.
Единицы измерения силы: ньютон (н) или килограмм силы (кГ), где 1н = 9.81 н. Статическое измерение сил осуществляется динамометрами.
Графически силы выражаются векторами (отрезком, длина которого соответствует модулю силы, а направление - направлению). Линия, вдоль которой направлена сила, называется линией действия силы.
Обозначения: Прописными буквами латинского алфавита , жирными F или чертой над буквой, модуль силы - |F|.
Система сил - совокупность сил, действующих на тело
Свободное тело - тело, не скрепленное с другими телами.
Если замена одной системы сил, действующей на тело, не изменяет его состояния покоя или движения, то такие системы сил называются эквивалентными.
Если система сил эквивалентна одной силе, то последняя называется равнодействующей
p.s. Возвращаясь к идее, изложенной во введении. Что означает это перенесение понятий одной научной области на другую. Теперь я понимаю, что меня постоянно останавливало: банальность. Тем не менее, с другой стороны, это не что иное, как создание универсального языка для какой-то области науки, отражающего общие закономерности, характерные также и для её объектов
И еще об одном: о способе употребления понятия силы: когда неизвестна сущность каких-то изменений, то придумывают специфическую силу для обозначения сущности, стоящей за ними. Но ведь когда говорят о силе, то ведь это не автономное, но системное понятие, которое предполагает понятия ускорения, скорости, пути, массы, времени. Другими словами, это принципиально динамическое понятие, описывающее движение. Но что такое движение? Это что, только наблюдаемое нами механическое движение? Конечно, нет. Всякий процесс представляет собой форму движения. И во всяком процессе нужно пройти путь от его начала, исходного пункта, до его конца, результата. Прохождение пути протекает во времени, и точки времени могут определяться точками процесса, как и точки процесса - точками времени. Иначе, процесс характеризуется скоростью, свой путь он может пройти быстрее или медленнее. В свою очередь, процесс может протекать неравномерно, характеризуясь, следовательно, ускорениями, а ускорение является изнаком действия силы
Значит, речь вовсе не должна идти о придумывании каких-то мифических сил - речь идет единственно о динамическом описании процессов, а это - вещь универсальная, верная для любой области.
Силы, действующие на тело, можно разделить на внешние и внутренние. Под внешними понимаются воздействия на частицы тела со стороны других тел, под внутренними - воздействие частиц тела друг на друга.
Переведем это на язык психологии: внешние воздействия - психологические воздействия людей друг на друга; внутренние воздействия - воздействие друг на друга психологических частей человека. И здесь уже несложно перейти от внешних воздействий к их отражению на внутренних силах человека, на том, какие силы в результате этого запущены и какие - компенсированы. И отсюда же получаем ответную силу воздействия субъекта на другие тела.
Сосредоточенная сила -сила, приложенная к телу в какой-нибудь одной его точке
Распределенные силы - силы, действующее на тело в целом или на какую-то его часть. Понятие сосредоточенной силы является условным и представляет собой равнодействующую некоторой системы сил. В частности, сила тяжести, действующая на тело, представляет собой равнодействующую сил тяжести его частей.
В психологическом плане наше ответное решение на воздействие, основанное на нашей приоритетной ценности, представляет собой равнодействующую по отношению к силе тяжести - Аксиомы статики
- Аксиома 1 Если на свободное абсолютно твёрдое тело действуют две силы, то тело может находиться в равновесии тогда и только тогда, когда эти силы равны по модулю (F1 = F2 и направлены вдоль одной прямой в противоположные стороны.
Соответственно, если на тело действует только одна сила, то тело в равновесии находиться не может.
Как это можно понять с психологической точки зрения? Во первых, на тело могут воздействовать две внешние силы, вызывая деформацию внутри тела, такую, что деформация одной силы компенсируется другой, и тело остается в равновесии. В то же самое время, можно допустить, что в теле формируются спонтанные психологические силы, воздействующие на внешнюю среду в соответствии с аксиомой 1. Возникает вопрос о формах равновесия и неравновесия психологического тела. Если имеет место внешнее воздействие, деформирующее психологическое тело, то в последнем возникает неравновесие. Признак деформации является признаком неравновесия. Психологическое тело способно восстановить равновесие в себе, развив соответственно собственную силу относительно воздействия и направив её в соответствии с аксиомой 1. - Аксиома 2
Действие данной системы сил на абсолютно твёрдое тело не изменитсяЮ, если к ней прибавить или от неё отнять уравновешенную систему сил.Отсюда следует, что две системы сил, отличающиеся на уравновешенную, эквивалентны друг другу
Следствие из 1-й и 2-й аксиом Действие силы на абсолютно твёрдое тело не изменится, если перенести точку приложения силы вдоль её линии действия в любую другую точку тела
Как это может быть понято психологически? То, что в математике не выступает в явном виде, а именно, отношение между непрерывностью и прерывностью, которое заключается в том, что мышление к непрерывности приходит через дискретность посредством понятия предела, то психологически дискретность выступает в явном виде, и непрерывность событий реализуется через их последовательную смысловую стыковку. Итак, непрерывность психологическая образуется последовательностью смыслов, которые носят принципиально дискретный характер. Тогда , единицей психологической реальности является элементарный смысл события. Соответственно, если мы имеем тождественные смыслы, то замена одного смысла тождественным содержания события не меняет.
Если исходить из такой предпосылки, то точки прямой должны пониматься как обладающие одинаковым смыслом, что соответствует модулю силы, и двумя противоположными направлениями, что соответствует модусу смысла, положительному или отрицательному.
Теперь рассмотрим доказательство следствия. Нас интересует здесь не доказательство само по себе, а применяемый аксиоматический геометрический метод мышления, включающий в себя наряду с собственно мышлением чувственно-содержательные конструирующие действия.
Пусть на тело в точке А действует сила F. Проведем прямую в соответствии с направлением силы F и выберем вдоль линии её действия в теле любую другую точку В и приложим к ней уравновешенную систему систему сил F1 и F2, равных по модулю силе F и имеющих одинаковое и противоположное с ней направление. Тогда сила F окажется уравновешена с одной из уравновешенных сил, F1 или F2 в соответствии с аксиомой 1. И тогда другая сила, F2 или F1 соответственно образует с исходной силой уравновешенную систему, и тогда останется одна сила, равная силе F, но приложенная в точке В.
Т.о., какие операции применялись: сначала, на основании аксиомы 2 в систему была добавлена уравновешенная система сил, ограниченная соответствующими условиями, связывающая чувственно участвующие в ней силы с исходной. Равновесие системы не изменилось. Затем была образована другая уравновешенная система, которую можно отнять, что и было сделано. И мы получили в результате снова одну силу
Речь до сих пор шла об абсолютно твердом теле, в котором не учитываются внутренние напряжения. Если мы возьмём стержень и приложим к нему уравновешенную систему из двух противоположных сил, то, произвольно перенося силы вдоль линии их действия мы получим варианты, когда силы будут воздействовать на стержень, сжимая его либо растягивая относительно приложенных точек. Этот вариант интересен психологически в том отношении, что характеризует противоположный характер внутренних напряжений деформируемого тела
Теперь мы можем сказать, что та цель, которая преследуется нами, это цель исследования процессов. Совершенно неважно, каких. Всякий процесс есть форма движения. Так как речь идет о процессах, то они обладают характеристиками, которые приложимы к любым их видам. Логика всех процессов одна. Во-первых, процесс - это какой-то "путь", это "перемещение от чего-то к чему-то" В этом смысле всякий процесс характеризуется "пространством", характерным для его специфической реальности. При этом само пространство характеризуется множеством координат.
Всякий процесс протекает во времени. Отношение между "путём", который должен пройти процесс, и временем, в течение которого этот путь процесс проходит, характеризует его скорость. "Пространство" любого процесса характеризуется множеством изменяющихся признаков. Каждый из изменяющихся признаков "пространства" соответствует его координате. Изменяющийся признак координаты соответствует "точкам" её "прямой".
Итак, во всяком процессе следует выделять множество независимых варьирующих признаков, что может быть изображено прямой и точками на ней от минимальных до максимальных значений признака в его положительных и отрицательных формах. Явление процесса представляет собой сложную систему признаков, выступающих как один признак. Соответственно, значениями каждого из признаков определяются траектории изменяющегося результирующего сложного признака. множество.
Затем, если мы имеем дело с процессом, то он возможен в той мере, в какой в нём действуют силы.
И вот здесь возникает один из существеннейших вопросов, связанный с принципами детерминизма и случайности. Нам представляется, что случайность - это не познанная необходимость, что все явления в мире связаны между собой детерминистически. Всё имеет свою необходимую причину и даёт необходимые следствия. Если так, то возникает представление, что в мире всё предопределено "от века", и если мы этого не знаем, то этого не знаем мы в силу ограниченности нашего знания. Однако я полагаю, что точно также, как изменяются вещи, точно также изменяются и законы. Что измененные вещи порождают изменение законов, которые, в свою очередь, порождают изменение вещей. И в этом смысле всё может быть всем.
Любой процесс протекает во времени. Что это означает с физической точки зрения? - "что невозможно возвратиться", то, что выражется словами "невозможно дважды войти в одну и ту же реку" Собственно, в этом заключается физическая сущность времени. Но если в основу времени положить этот принцип, то окажется, что на самом деле есть единство между "можно и нельзя" возвратиться. Существует даже феноменологическое ощущение возврата в прошлое, в реальность, которая когда-то уже была и теперь только повторяется. Мы погружаемся в ту же самую реальность, в те же самые ощущения и, следовательно, в то же самое время. Самый простой пример обыденной жизни - это то, что можно назвать "исправлением ошибок": осуществленное действие даёт нам реальность, которую мы рассматриваем в качестве ошибочной. Существуют ситуации, для которых "возврата нет", но гораздо чаще мы имеем возможность возвратиться в начальные условия процесса и повторить его заново. Вот теперь и можно поставить вопрос о направлении времени: откуда мы знаем, что время имеет только одно направление, по чему мы судим, на основании какой реальности? Если у нас есть часы, то о движении времени мы можем судить по движению стрелки часов. Об односторонности движения времени можно судить по тому, что мы стареем, а вот обратного процесса что-то не наблюдается. Вот если бы мы могли молодеть, то что? А ведь мы в этом случае были бы способны изменять своё собственное, реальное время. Что явилось бы причиной этого? - то, что процесс изменил своё направление.
И вот тут возникает следующая мысль: особенность процессов - в их направленности. Всякий процесс для данных условий есть переход от чего-то к чему-то. Для того, чтобы это стало возможно, должны существовать соответствующие силы, являющиеся двигателем процесса. А отсюда мы переходим к принципу определенности. Если представить себе, что нет определенности, то ведь в этом случае не будет и времени, ничего не будет, потому что если хоть что-нибудь будет, то это уже какая-то определенность. В этом смысле любое бытие оказывается основанным на определенности. Всякое бытие реально в той мере, в какой оно определено.
Что же получается? Время двойственно. Если у нас есть память и есть часы, к которым мы можем "привязывать события", то, формально говоря, мы можем выстроить бесконечную их последовательность, направленную из прошлого в будущее. Мне кажется, это то, что называют дурной бесконечностью. В то же самое время, психологически время индивидуально, и это отражается в ощущениях: мы можете чувствовать, что идете вперед, что остановились, что оказались в прошлом. Вы можете физически ощущать время и скорость его течения, которые изменяются в соответствии с вашими импульсами деяттельности. Наконец, вы можете не ощущать времени.
И есть еще один вопрос - об источниках сил. С одной стороны, имея дело с механикой, мы видим, что тела взаимодействуют, передавая движения. Но если мы рассмотрим землю по отношению к земным телам, то мы видим её гравитационное влияние на них. Источником силы оказывается земля. С другой стороны, если мы возьмём субъекта, то на него, разумеется, воздействуют силы, которые он так или иначе отражает своим поведением. И т.о. мы приходим к принципу детерминизма. Но ведь это - позиция, которая в качестве начала движения психологического тела рассматривает воздействие на него. Но ведь можно перевернуть это отношение, и тогда окажется, что источником силы является субъект. Субъект способен к порождению силовых влияний, и какими они окажутся, это большой вопрос, потому что они могут быть как простой реакцией на воздействие, так импульсы со стороны субъекта в отношении внешней среды могут быть связаны с непредсказуемыми мутациями в его психологическом теле в силу процессов, которые невозможно отследить. Я уж не говорю об идее Бога, которая позволяет оправдать любую случайность как проявление его воли. Поэтому принцип детерминизма, безусловно, является единственным орудием науки, который позволяет человеку овладевать природой. Однако он открывает перед нами лишь небольшую видимую часть айсберга реальности. - Аксиома 3 (аксиома параллелограмма) Две силы, приложенные к телу в одной точке, имеют равнодействующую, приложенную к той же точке и изображаемую диагональю параллелограмма, построенного на этих силах как на сторонах.
- Аксиома 4 При всяком действии одного материального тела на другое имеет место такое же по величине, но противоположное по направлению противодействие.
Закон о равенстве действия и противодействия является одним из основных законов механики. Из него следует, что если тело А действует на тело В с силой F, то одновременно тело В действует на тело А с такой же по модулю и направленной вдоль той же прямой, но в противоположную сторону силой F`=-F Однако силы F` и F не образуют уравновешенной системы, так как они приложены а разным телам.
Нетрудно наблюдать выполнение этой закономерности также и для психологических тел: вы можете видеть на самих себе, что непосредственная ваша реакция на любое неожиданное воздействие оборонительная, направленная на восстановление статус кво: действию на вас вы противопоставляете ответное точно такое же воздействие, определяющее прямую воздействия, причем, не имеет значение направление воздействия на вас, то есть его значение - является оно положительным или отрийцательным. Благодаря этой вашей реакции вы восстанавливаете ваше положение во внешней среде. А так как существует непосредственная связь между равновесием психологического тела с внешней средой и равновесием в его внутренней среде, то вы, оказывая противодействие изменениями в отношениях с внешней средой, тем самым сохраняете схему равновесий в своей внутренней среде. При этом внутри системы возникают внутренние напряжения, не нарушающие равновесия в системе, которыми обеспечивается поддержание отношений с внешней средой. Эта связь между внутренними и внешними силами для психологического тела является существенной. Между тем в практике социальной жизни внутренние силы обычно не принимаются во внимание, то есть с точки зрения общей механики психологическое тело рассматривается как абсолютно твёрдое тело, то есть как представляющее собой уравновешенную систему, которую можно отбросить, что позволяет ограничиваться рассмотрением только внешних сил, действующих на психологическое тело. - Аксиома 5 (принцип отвердевания) Равновесие изменяемого (деформируемого) тела, находящегося под действием данной системы сил, не нарушится, если тело считать отвердевшим (абсолютно твёрдым) или,
другими словами, при равновесии силы, действующие на любое изменяемое
(деформируемое) тело, удовлетворяют тем же условиям, что и для тела
абсолютно твёрдого, однако для изменяемого тела эти условия, будучи необходимыми, могут быть недостаточными.
Например, для равновесия нити под действием двух сил, приложенных к её концам, необходимы те же условия, что и для жесткого стержня, но они недостаточны, так как эти силы должны быть направлены в противоположные стороны, то есть быть растягивающими - Связи и их реакции
- Свободное тело - тело, которое не скреплено с другими телами и может совершать из данного положения любые перемещения в пространстве.
Несвободное тело - тело, перемещениям которого в пространстве препятствуют другие скрепленные с ним или соприкасающиеся с ним тела.
Связь - всё то, что ограничивает перемещения данного тела в пространстве.
Имея дело с психологическими телами, следует определять связи, которыми обусловливаются ограничения их движений в психофизическом пространстве. При этом следует иметь ввиду психологический и физический аспекты связей. Под психологическими (субъективными) связями следует понимать рефлекторные схемы, проявляющие себя в установках, взглядах, убеждениях, ограничивающие возможности движения. Под объективным аспектом связей понимается физическая невозможность перемещений в психофизическом пространстве.
Пример субъективной связи: В "Горе от ума" Платон Михалыч, сопровождает жену на балы, не желая этого, хотя и имеет возможность это не делать . С другой стороны, здесь же налицо проявление инертности, характер человека, который ведет себя так, как требует от него среда. Социофизические связи: "Связь Анны Карениной с Вронским делает для неё невозможным открыто видеться с сыном. Существует связь между объективным и субъективным аспектами: Невозможность видеться с сыном связана с субъективной реакцией её мужа на её измену, которая реализовала себя в запрете посещений Анной сына.
Итак, рассматривая события, мы должны для их понимания исследовать объективные и субъективные, внешние и внутренние связи.
Внешние связи - другое название для объективных связей.
Внутренние связи - другое название для субъективных связей.
Сила давления на связь - это сила, с которой тел, стремящееся осуществить перемещение под влиянием действующих на него сил относительно препятствующей движению связи.
- Свободное тело - тело, которое не скреплено с другими телами и может совершать из данного положения любые перемещения в пространстве.
- Действия тел друг на друга, создающие ускорения, называют
силами. Все силы можно разделить на два основных типа: силы, действующие при непосредственном соприкосновении, и силы, которые действуют независимо от того, соприкасаются тела или нет, т. е.
силы, которые могут действовать на расстоянии.
Для того чтобы одно тело могло действовать на другое при непосредственном соприкосновении, первое должно быть в особом состоянии: чтобы рука действовала на мяч, мышцы руки должны быть сокращены; чтобы действовать на пробку игрушечного пистолета, воздух или пружина должны быть сжаты, и т. д. Сжатия, растяжения, изгибы и т. п.— это изменения формы или объема тел по сравнению с их исходным состоянием. Такие изменения называют деформациями и при наличии таких изменений говорят, что тело деформировано. Мышцы, пружины, газ и т. п. должны находиться в деформированном состоянии, чтобы действовать на соприкасающиеся с ними тела с некоторой силой. Эти силы в большинстве случаев действуют только до тех пор, пока тела деформированы, и исчезают вместе с исчезновением деформаций. Такие силы называют упругими. Кроме упругих сил, при непосредственном соприкосновении могут возникать еще и силы трения. Примеры: сила трения между бандажом колеса железнодорожного вагона и прижатой к нему тормозной колодкой; сила трения, действующая на тело, движущееся в вязкой жидкости («сопротивление среды»).
Обычно при рассмотрении психофизических явлений мной употреблялось понятие соответствия или рассогласования. Понятие деформации представляется психологичным в том отношении, что оно имеет в себе динамическое содержание, которое порождает движение. В этом смысле для того, чтобы было получено поведенческое движение, необходима соответствующая психологическая деформация субъекта.
Для сил, действующих на расстоянии, нет такой простой картины взаимодействия тел, как для упругих сил. Важнейший пример сил, действующих на расстоянии,— силы всемирного тяготения и, как частный случай, сила тяжести (сила земного притяжения). Падение тела, т. е. наличие ускорения, направленного вниз, у тела, поднятого над Землей и предоставленного самому себе, показывает, что со стороны Земли на него действует сила, хотя во время падения тело и не соприкасается с Землей.
Магнит действует на другой магнит, находящийся от него на некотором расстоянии.
Силы всемирного тяготения, действующие между предметами нашей обыденной жизни, ничтожны по сравнению с остальными силами, действующими между ними. Например, резиновая нить длиной в 1 м и поперечником в 1 мм, растянутая всего лишь на 1 мм, действует с силой упругости, в миллионы раз превосходящей силу взаимного тяготения между двумя килограммовыми гирями, стоящими на расстоянии 1 м друг от друга. Но если одно (или оба) из притягивающих тел — это огромное небесное тело, силы всемирного тяготения также делаются огромными. Так, Земля притягивает килограммовую гирю в 1011 раз сильнее, чем притягиваются гири в приведенном примере, а Солнце притягивает Землю в 4*1021 раз сильнее, чем Земля притягивает гирю.
Кроме сил тяготения, на расстоянии действуют также магнитные и электрические силы. Если к магниту, плавающему в воде на поплавке, приблизить другой магнит так, чтобы они не соприкасались друг с другом, то магнит на поплавке приобретет ускорение и либо начнет приближаться ко второму магниту, либо оттолкнется от него, в зависимости от взаимного расположения их полюсов (рис. 54). Электрически заряженные тела, находясь на расстоянии друг от друга, притягиваются или отталкиваются в зависимости от того, разноименны или одноименны их заряды.
4.1 Пискунов Н.С. Дифференциальное и интегральное исчисления м., "Наука", 1985
4.2 Бронштейн И.Н., Семендяев К.А Справочник по математике М., "Наука", 1980
4.3 Выгодский М.Я. Справочник по высшей математике М., "Наука", 1977
- С субъектом связываются разные системы координат
На рис. 1 представлены декартовы прямоугольные и косоугольные координаты на плоскости.
Положение точек наглядно представлено пересечением соответствующих клеточек.
Начало координат совмещается с каким-то объектом, вид же координат может быть соотнесен с видом пространства соответствующего объекта и, соответственно, с теми значениями, которыми обладают другие объекты в его системе координат. Если рассматривать субъект как психофизический объект с доминированием в нём психических свойств, в силу чего его можно рассматривать как психическое тело, то можно допустить, что с каждым из субъектов связано его пространство (скажем так, излучаемое им психологическое пространство). Эти пространства могут различаться своими линиями в соответствии с конкретной формой координатной системы тела, и тогда возникает вопрос о том, как выглядят одни объекты "в глазах" других. В связи с возникающим в этом случае множестве оценок одной и той же реальности возникает вопрос о приведении этого множества "взглядов" к "общему знаменателю" путём выделения во множестве объектов такого, в значения пространства которого переводятся значения пространств всех других тел. Благодаря этому достигается возможность получения общего языка для всех тел. - Движение, пространство, время
Представим себе, что деревня А - объект, по отношению к которому строится система координат. Проведем прямую от деревни А к деревне В, и от точки А проведем прямую в -90 градусов, которую назовем абсциссой 0х, и вторую линию - ординатой 0у. Теперь Представим себе, что в полученной координатной системе движется машина, образуя траекторию движения, подобную показанной на рис. 2.
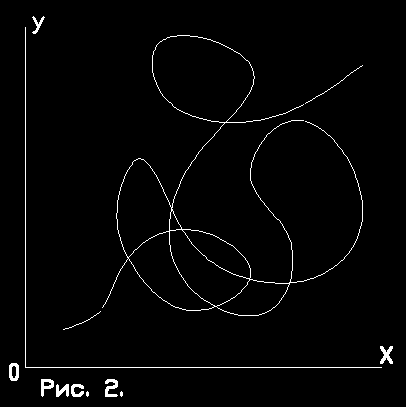Какую особенность мы наблюдаем? Ту, что при фиксированном значении одной переменной (х или у) мы можем получить
множество значений другой. Т.о., если мы станем непосредственно интерпретировать полученный график, то возникает представление, что машина может одновременно находиться в разных точках. Из чего у нас возникает такой взгляд? из непосредственно наблюдаемого нами факта, из той реальности, которая находится у нас перед глазами. А что такое эта реальность? Это тот след, который оставила машина в результате движения. Этот след существует как целое, одновременно, точнее, параллельно существующее во всех своих точках.
Теперь проведем перпендикуляр 0t из точки 0 плоскости х0у в положительном направлении и будем считать, что это - линия времени. Если мы теперь начнём рассматривать рисунок, то что мы получим? Мы получим, что в результате движения машины в каждый следующий момент времени её движения совершается переход к другому пространству, точнее, к другой его форме х0у. Вследствие движения машины пространство с каждым моментом времени изменяется. До тех пор, пока машина стояла неподвижно (будем считать, что машина - единственный могущий изменяться фактор пространства), пространство оставалось тем же самым, и времени в силу этого не существовало. Время возникло только в момент, когда машина начала движение. Другими словами, время возникает с движением.
Что такое изменение пространство с дискретной точки зрения? это непрерывная замена одного пространства другим, какое-то приращение в существующем исходном пространства, положительное или отрицательное.
Итак, мы имеем какое-то начальное состояние пространства и конечное его состояние. А что же представляет собой любое его промежуточное состояние. взятое само по себе и рассматриваемое относительно момента времени. Понятие момента времени равносильно понятию предела. Это момент времени, когда позади оставлено прошлое и впереди еще нет будущего. То есть это какое-то маленькое приращение, маленькая новая произведенная реальность. И всё.
Теперь обратим в связи с этим внимание на другую сторону дела - на часть пространства, которая остаётся вне изменения. Так как в ней отсутствует движение, то в ней отсутствует и время. Т.о., мы получаем двойственность, противоречие между движением и его отсутствием вот в каком смысле. Во всякий момент времени движение производит свой результат, который, в предположении, что он не изменяется, существует как неизменная вещь и поэтому не принадлежит времени. Но если движение производит результат, то произведенный результат не есть движение, притом, что формально мы получаем форму, или видимость движения, потому что мы видим, как движение, порождая собой всё новые и новые результаты, создает в результатах новую форму пространства. Но в таком случае как это можно себе представить? Только так, что каждому моменту времени соответствует своя форма пространства. Это получается как бы бесконечная пачка пространств, такая, что в каждой из них присутствует лишь результат, который получен в данный момент времени, лишь та преобразованная, переработанная часть пространства, которая следует вслед за предшествующим моментом времени. И только. Т.о. мы имеем дело с таким положением вещей, при котором вся постоянная, неизменная часть пространства остается существовать вне времени. Все новые точки пространства, полученные в результате движения в нём, представляют собой такие же вневременные точки пространства, как и остальное существующее не подвергающееся изменению пространство. Т.о. в результате движения автомобиля мы получаем бесконечное множество пространств, которыми представляется целое, лишь когда мы смотрим на результат как бы через бесконечное множество пространств, которые вместе дают картину целого нового преобразованного пространства, в данном случае пространства со следом от колес автомобиля.
Т.о., что мы получили? - то, что мы рассматриваем как одно пространство, на самом деле представляет собой бесконечные множества пространств, порожденных движением. Так ведь, которая нами ощущается "как одно", на самом деле представляет собой то бесконечное множество пространств, которые оставляет после себя движение. И то, что это так, доказывается тем, что в случае обратного преобразования пространства мы наталкиваемся на бесконечное множество пространств; Мы не можем возвратиться в исходную точку, не преодолев весь обратный путь, не сняв порожденное предшествующим движением новым, обратным движением.
Этим обусловливается отношение между изменчивостью и постоянством, а также понятие конечной скорости изменчивости или время жизни постоянного.
Итак, время - это категория, принадлежащая движущемуся объекту. А если это так, то время движущегося объекта изменяется в соответствии с характеристиками движения объекта. С субъективной точки зрения это может быть представлено т.о., что чем медленнее движение, тем медленнее течет время, и чем более интенсивным является движение, тем быстрее течет время. В качестве характеристики времени можно выделить его скорость, в том числе и отражение ощущения её в субъективной реальности человека.
Следующий вопрос, с которым мы сталкиваемся - так как время - реальность движущегося объекта, а объектов множество, причем. они характеризуются разными свойствами времени (свойствами часов), то возникает вопрос об отношениях разных свойств времени. В связи с этим, возникает понятие синхронизации различных времен, насколько это возможно, а также задача перевода времени одних объектов во время других. - Функциональный принцип
Функциональный принцип заключается в рассмотрении изменений одной величины в зависимости от изменений другой.- Определение
- "Если каждому значению переменной х, принадлежащему некоторой области, соответствует одно определенное значение переменной у, то у есть функция от х или, в символической записи, y = f(x)."
- Замечание
- "Иногда в определении понятия функции допускают, что каждому значению х , принадлежащему некоторой области, соответствует не одно, а несколько значений у. В этом случае функцию называют многозначной в отличие от определенной выше функции, которую называют однозначной." [4.1, 20]
Значение функционального принципа состоит в первую очередь именно в получении однозначности, исключении неопределенности.
Линии 0а, 0b, 0c различаются наклоном, однако, какой бы интервал мы ни взяли, отношение между величиной аргумента и функцией будет постоянным. Тогда как всякая кривая представляет собой синтез бесконечного множества наклонных, являющихся касательными к точкам кривой и определяемых как тангенс соответствующего угла tg a (рис.3)
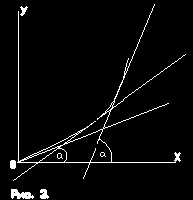Исходная мысль такая: C геометрической точки зрения формулы вида s=vt, v=at и т.д. представляют собой просто линейные функции, и поэтому могут интерпретироваться одинаково, то есть выражение вида v=at может рассматриваться также как своеобразный путь, то есть v -это также с какое-то перемещение, как и выражение s=vt.
Пусть s=vt; тогда если для всякого t`-t=∆t s`-s=∆s таково, что v = (s`-s)/(t`-t)=∆s/∆t = const, мы имеем движение с равномерной скоростью. Но v точно также может рассматриваться как путь, который v проходит за время ∆t, то есть v=v`t: в свою очередь v` также есть путь ∆v, который оно проходит: v`= v``t. Пусть v`` = t, тогда v```=1. Отсюда получаем: s = vt = v`tt=v``tt=ttt=t3 Здесь всюду мы совершали переходы от одной равномерности к другой: равномерная скорость, равномерное ускорение, равномерное ускорение ускорения и т.д. При этом равномерное ускорение ускорения дает неравномерное ускорение, неравномерное ускорение порождает неравномерную скорость следующего порядка.
s=vt;
v=v`t;
v`=v``t;
...
Итак, важнейшим во всём этом являются понятия равномерности и неравномерности. Равномерная скорость – что такое равномерная? – это какая-то постоянная. Путь – вещь переменная. Но скорость- это постоянная. Что даёт нам путь как линейную функцию от времени. Если мы говорим о равномерной скорости, то значит ускорение – это постоянная. И это означает также, что путь при этом будет идти с неравномерной скоростью. То есть сама смена скорости, то есть ускорение, равномерно, но движение в пути неравномерно. Т.о., во всяком случае на практике, мы всегда где – то в конечном счете заканчиваем равномерностью, какой-то постоянной. Например, пусть ускорение а равно 2. Но здесь, очевидно, нужно обращаться к интегрированию. Тогда получаем 2х+с, где С – это начальные условия. Теперь допустим, что у нас равномерным является ускорение. То есть ускорение ускорения равно постоянной, ускорение – это линейная функция. Скорость – это функция от t, в которой в качестве функтора выступает коэффициент пропорциональности. И т.о. получаем кt2. А отсюда мы уже получаем формулу пути: s=vt=kt2t=kt3
Что представляет собой к? Оно представляет собой признак равномерности, характеризующий высшую степень ускорения. Например, a`=6 → a = 6t → v = 6t2 → s=6t3
Теперь такая мысль. В математике изучение анализа начинают с понятия производной и затем переходят к понятию первообразной. В этом случае мы, получив производную функции, затем переходим к первообразной, и полученный результат должен совпадать с исходным пунктом движения. Можно видеть, что в моём частном примере движение идет, напротив, от некоторой производной к первообразной, и это движение должно дополняться противоположным движением от первообразной к производной. Исходя из принципа построения обратного действия на основе прямого, мы получаем: дано: s=kt3. Функция от t. Следовательно, она может быть переписана в виде s=kt2t, где t - аргумент функции s, а выражение кt2 в свою очередь есть производная функция, которая выражает отношение s/t. То есть можно записать v = s/t=kt2 Соответственно, применяя тот же приём к выражению v=kt2 получаем а=v/t=kt. Мы видим, что одни и тот же аргумент t появляется в выражении несколько раз. И, наконец, получаем a`=a/t=k=const. Мы видим, что в настоящем случае мы не применяли понятия предела
Пусть s=vt, где v=const, т.е. v=s/t=const для любых значений t, откуда s=(s/t)t. А что это означает? - то, что в выражении s/t мы t можем придавать любые значения, при этом отношение меняться не будет.
Запишем выражения:
1.равномерное движение
2.равномерное ускоренное движение;
3. равномерное ускорение ускоренного движения
5. и т.д.
1.
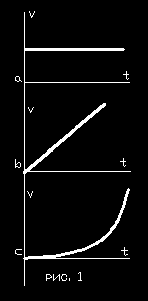Возьмём формулу: s=vt. 1.Движение равномерное, скорость постоянна, следовательно, функция пути от времени является линейной.
s=kt, где к - const.
Производная от постоянной равна нолю, чем выражается независимость скорости от времени. (рис.1а)
2.Движение равномерно ускоренное. Скорость зависит от времени, поэтому можем записать:
s=vt=v(t)t (рис.1b) Согласно допущению, скорость может интерпретироваться так же, как путь. Затем, скорость изменяется равномерно. Следовательно,
v(t)=kt,
откуда в случае равномерно ускоренного движения получаем
s=ktt=kt2
3.Равномерное ускорение: (рис.1с) s=vt; v(t)=a(t)t=ktt=kt2; s=vt=kt2t = kt3
Но:
1. s=kt; s+∆s=k(t+∆t); ∆s=k(t+∆t)-kt = k(t+∆t-t)=k∆t; ∆s/∆t=k∆t/∆t=k;
2. s=kt2; s=k(t+∆t)2 = k(t2 + 2t∆t + ∆t2); ∆s=k(t2 + 2t∆t + ∆t2) - kt2 = 2t∆t + ∆t2; ∆s/∆t=k(2t∆t + ∆t2)/∆t = 2kt;
Получается, что я исходил из производной kt, а букварь исходит из производной 2кt, или в общем случае получается, у меня производная kхn= xn-1, а в букваре knxn-1
Обратимся к геометрическому истолкованию производной.
Пусть на плоскости есть произвольная кривая. . Выберем на ней две точки М0 и М1 и проведем через них прямую. Точку М1 сделаем скользящей и направим её в сторону точки М0. Представим себе, что точка М1 инерционная, а точка М0 обладает притяжением. Тогда точка М1, поколебавшись вокруг точки М0, совместится с ней. При этом прямая М0М1... в каком положении она окажется? До тех пор, пока между точками М0, М1 есть минимальное, сколь угодно малое расстояние, прямая М0М1 фиксирована. Как только точки совпадут, она лишается ориентации на плоскости. Поэтому не говорят, что точки М0, М1 совпадают, но что точка М1 неограниченно приближается к точке М0 с любой стороны. Такую прямую называют касательной к точке М0, Она образует угол α с положительным направлением оси абсцисс.
С другой стороны, кривая- это какая-то функция y=f(x), точке М0 соответствует значение аргумента х0, точке М1 - значение х1, а их разность - приращению ∆х. Соответственно, значениям аргументов соответствуют значения функции, а разности значений функции соответствуют её приращения. Откуда получаем: tg α = (∆y/∆x), и при устремлении ∆х к нолю мы получаем соответствующее изменение ∆у и их отношение как значение производной.
"Отсюда f`(x) = tg α, то есть значение производной f`(x) при данном значении аргумента х равняется тангенсу угла , образованного с положительными направлением оси координат 0х касательной к графику функции f(x) в соответствующей точке М0(х,у)" [4.1, 72]
Т.о., речь идет о касательной к точке на графике а на самом деле мы имеем дело с двумя точками, однако настолько близкими друг к другу, что их на практике можно принять за одну точку. Другими словами, мы продолжаем иметь дело в реальности со средней скоростью, которая может быть сколь угодно близкой к скорости мгновенной. И, значит, мы имеем дело не с актуальной, а с потенциальной точностью. Мы продолжаем иметь дело в действительности не с одной касательной, а с двумя, и не с одним углом, а с двумя, которые могут сколь угодно близко приближаться друг к другу, но никогда не могут совпасть. Так что здесь, конечно, с формальной точки зрения мы имеем дело с подменой понятий. С другой стороны, мы имеем дело с количественным изменением, которое даёт якобы качественный скачок: вместо двух разных углов α0, α1мы говорим об одном угле α0.
Имея дело с кривой, представляющей функцию, мы при приращении аргумента получаем изменения в положении касательной и, сл., угла α и отношения tg α.
Итак, в разных точках кривой мы получаем разные наклоны касательно, которая представляет собой линейную функцию. Так, в соответствии с формулой (x
Между тем я в моих рассуждениях получал кх, а не 2х. Другими словами, "к" мной не было определено. При этом я очевидно предполагал, что коэффициент "к" можно задавать произвольно, то есть я не использовал понятия касательной к точке, положение которой изменяется от точки к точке. С другой стороны, если рассматривать класс функций хn, то очевидно, что в зависимости от значения n находится скорость изменения функции и, соответственно, "крутизна" кривых графиков функций, в качественном отношении одинаковых, но различающихся только количественной стороной. Следовательно, существует связь между показателем функции и углом наклона α касательной. Возникает вопрос: какого рода эта связь? Возвратимся к функции s=vt=kt2 и определим угол наклона касательной в точках 2 и 5. Целью нашей является определить значение коэффициента "к" линейной функции, представляющей скорость изменения.
| t | s | ∆t | ∆s | ∆s/∆t |
| 2 | 4 | |||
| 3 | 9 | 1 | 5 | 5 |
| 2,1 | 4,41 | 0,1 | 0,41 | 4,1 |
| 2,01 | 4,04 | 0,01 | 0,04 | 4 |
| 2,001 | 4,004 | 0,001 | 0,004 | 4 |
| t | s | ∆t | ∆s | ∆s/∆t |
| 5 | 25 | |||
| 4,9 | 24,01 | 0,1 | 0,9 | 9 |
| 4,99 | 24,9 | 0,01 | 0,1 | 10 |
| 4,999 | 24,999 | 0,001 | 0.01 | 10 |
Возникает вопрос: почему показатель степени функции "пути" становится коэффициентом линейной функции "скорости"? Обратим внимание вот на что:
0.11=0.1;
0.12=0.01;
0.13=0.001;
0.14=0.0001
или
101=10
102=100
103100
и т.д.
Мы видим, что последовательное изменение степени переменной в степенной функции изменяет получаемое значение на порядок. Но в рассмотренной нами схеме отношений пути, скорости, ускорения и т.д. имеет место именно это смещение порядка. Отношение между равномерным движением и движением с ускорениями разного порядка заключают в себе качественное различие, так как операции с линейными функциями - это операции, качественно отличные от операций с функциями нелинейными. Мы всюду видим, что в конечном счете нелинейные функции исследуются путём применения к ним линейных. То есть линейные функции являются средством, орудием, при посредстве которого исследуются всевозможные проявления действия сил. Для этой цели используются вспомогательные понятия - потенциальной или актуальной бесконечности, предела, бесконечно малой. Во всех этих случаях "инертность" линейной функции дополняется процессами движения, изменения. Кажется, что линейная функция представляет движение. Но это - "мёртвое движение" в противовес "живому" Всё это ведет к следующей идее, реализованной преобразованиями Лапласа и Фурье. [6.1,520-521]
Преобразованием Лапласа называется преобразование некоторой функции вещественной переменной t, называемой оригиналом в другую функцию F(p) комплексного переменного р, называемую изображением. Оно позволяет заменить дифференцирование и интегрирование оригиналов более простыми операциями умножения и деления с изображениями.
- Комплексаные числа
- z=x+iу
Непонятно, почему употребляется знак плюс, ведь х,у обозначают точку на
плоскости. Но: если точка z плоскости есть х1, у1, то прямая, соединяющая начало координат и точку, имеет модуль |z|=(x2+y2)1/2
i = -11/2, совмещается с осью ординат. Что представляет собой мнимая ось, какого рода числа содержит?
- Показательная функция с комплексным показателем и её свойства
- Пусть z=x+iy. Если х и у - действительные переменные, то z называется комплексным переменным. Тогда возникает вопрос, что представляет собой выражение iy. Что такое i - это корень из минус единицы. И это число умножается на действительное число. Тогда, обобщая, мы можем сказать, что есть какая-то система чисел, в которой действует правило
- Корень из -1 ( Эбралидзе Арчил Арчилович. http://zhurnal.lib.ru/e/ebralidze_a_a/286.shtml)
-
Как были получены мнимые числа?
Сначала было введено сложение.
2+2=4
Затем умножение, которое по существу тоже является сложением.
2х3=2+2+2
Затем возведение в степень, которое по существу тоже является сложением.
2в тр.ст.=2х2х2=2+2+2+2
Затем или одновременно с этим, не знаю хронологическую последовательность, были введены отрицательные и положительные числа.
Далее начали оперировать с новыми числами.
Условились, что
(-5)х(-5)=+25
(+5)х(+5)=+25
(-5)х(+5)=-25
Таким образом
(-5)х(-5)=+25
(+5)х(+5)=+25
То есть положительное число, умноженное само на себя, дает положительное число.
Отрицательное число, умноженное само на себя, дает положительное число.
Числа, которое при умножении само на себя, дает отрицательное число, нет.
Корень из положительного числа может быть и положительным, и отрицательным.
Извлекать корень из отрицательного числа бессмысленно.
Тем не менее математики решили извлечь корень из отрицательного числа. Возможно, они исходили из глубокой мысли, что поскольку в математике есть и отрицательные числа, и знак корня, их надо совместить из этого непременно выйдет толк.
Извлечь корень из отрицательного числа, то есть найти, какое число, умноженное само на себя, дает отрицательное число, не удалось, так как математики сами условились, что таких чисел нет.
Тогда математики сделали, что могли.
Представили отрицательное число в виде произведения положительного числа на -1, извлекли корень из положительного числа, надеясь, что проблема таким образом упростится и что с -1 они что-нибудь придумают.
кор.из(-25)=кор.из/(+25)(-1)/=кор.из(+25)хкор.из(-1)= +-5хкор.из(-1)
Осталось совсем немного.
Извлечь корень из -1.
Однако найти какое число, умноженное само на себя, дает -1 не удалось по той же самой причине.
Но если нельзя найти, то можно обозначить кор.из(-1) через i.
Таким образом,
кор.из(-25)=+ -5хкор.из(-1)=+ -5i
То есть корнями из -25 являются +5i и -5i.
Эти результаты были названы мнимыми числами.
Надо сказать, что хотя i внушает больше доверия, обозначает оно ничто иное, как кор.из(-1).
Разница в том, что когда пишут -1, достаточно очевидно, что математикам не удалось ни найти, какое число, умноженное само на себя, дает кор.из(-1), ни разумно объяснить ситуацию, а когда пишут i, эта проблема завуалирована.
Найти число не могут потому, что сами договорились, что таких чисел нет.
- Сложение и умножение
- Последуем за А.А.:
Сложение: 2+2. Например, двое ножниц и две овцы. Если это просто объекты, то получаем 4. Но если учитывается качество объектов, то сложение теряет смысл, т.к. мы имеем дело с разными, не пересекающимися множествами. Единственное, что здесь можно добавить, хотя это относится к другой идее, то если ножницы предназначены для стрижки овец, то можно говорить об установлении соответствия между овцами и ножницами, то есть об установлении соответствия между мощностями двух множеств. Но это уже из другой оперы. Мы видим, что для того, чтобы иметь возможность складывать элементы множества, нужно подвести его по общий род. Значит, складываться могут только объекты одного рода. Только в этом случае мы имеем дело с количественным отношением.
Умножение: 2*3=6. Умножение сводится к сложению: 2+2+2 либо 3+3 Мы видим, что слагаемые в приведенных примерах играют разную роль: одно слагаемое выступает в качестве множества, представляющего объекты какого-то рода. Второе слагаемое указывает на то, сколько раз следует множество. То есть второй элемент как бы элемент, производящий множества. В результате мы получаем мощность нового множества, включающего в себя все элементы исходного множества. Например, человек в неделю получает 100 долларов. Сколько он получит в месяц?
Увеличение числа слагаемых ничего не меняет в сути дела: всегда есть множество исходных объектов, которые тиражируются сколько-то раз, получается новое множество, включающее в себя все элементы тиражированных множеств. Полученное множество в свою очередь тиражируется сколько-то раз, получается новое множество, и т.д.
Умножение сравнительно со сложением характеризуется тем, что занимается сложением объектов одного и того же тиражируемого множества. То есть если сложение допускает сложение разных множеств одного рода, то умножение имеет ввиду одно и то же множество. Например, дневной рацион питания солдата должен заключать в себе столько-то граммов животных жиров, мяса, круп и т.д.. Теперь это множество ставится в соответствие с каждым элементом множества солдат. Что отсюда мы получаем? - умножение двух множеств, таких, что каждому элементу одного множества ставится множества ставится множество элементов другого множества. Если мы в связи с этим введем принцип соответствия, то множества свойствам элемента, потому, что суточный рацион питания солдата определяется его потребностями в пище, то мы получим, что исходное множество образовано на основе потребностей другого множества. В свою очередь, множество солдат существует постольку, поскольку оно создается в соответствии с потребностями, то есть свойствами другого множества, и т.д.
Итак, пусть есть два множества элементов А, В. Множество А={a1, a2, a3} B = {b1, b2}. В обоих множествах элементы ai, bj, где i=1,2,3, j=1, 2 - отдельные объекты, следовательно, суть единицы, поэтому в самой записи множества можно указать на операцию сложения как получение его мощности. Тогда множества перепишутся так: А={a1+ a2+ a3} B = {b1+ b2}, а умножение даст: C= A* B = a1 * (b1+ b2) +a2 * (b1+ b2) + a3 * (b1+ b2) = {a1b1 + a1b2 + a2b1 + a2b2 + a3b1 + a3b2} Очевидно, что мощность множества mA=3, множества В mB=2, а произведение равно 6. Однако мы видим, что технология получения произведения не является совсем простой.
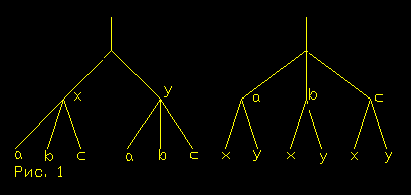
На рис.1 показано, что технологический процесс умножения может быть представлен в форме дерева, если исходить из данной нами выше интерпретации умножения. Но в то же самое время из множества путей дерева видно, что в результате умножения мы получаем сложные объекты, представляющие собой некий симбиоз множеств, так как элементы a1b1, a1b2 и т.д. - ведь это не простая форма соответствия между элементами множеств, но это прежде всего отношение принадлежности одних элементов другим элементам, причём, это отношение может быть взаимным, как при умножении, что показано на примере деревьев рис.1. Между тем, в самом результате умножения мы не обнаруживаем ничего, кроме простого неопределенного тиражирования исходных объектов и их суммирования, которое и даёт нам искомый результат умножения; в нем не показывается, по отношению к чему получается такой результат.
Если условно принять, что умножение выполняется последовательно слева направо и первое слагаемое представляет исходное множество элементов, над которыми производятся операции, то все последующие сомножители указывают на число множеств тиражируемых элементов. В этом случае мы получаем последовательное построение дерева снизу вверх.
Но во всех этих случаях знака чисел практически нет, потому что о положительном числе можно говорить только тогда, когда есть отрицательное число, причем, по большому счету, нет как такового положительного и отрицательного, а есть противоположные числа. Отрицательное же и положительное в субъективном смысле - это уже относится к интерпретациям чисел. С другой стороны, понятие отрицательных и положительных чисел также может рассматриваться как как непрерывное движение от минус к плюс бесконечности.
- Объект и признак
- В логике есть правило: признак признака предмета есть признак самого предмета. Я хочу здесь обратить внимание вот на отношение понятия объекта и признака объекта. Объект является через свои признаки. Если рассматривать объект как вещь, которая обладает множеством признаков, то можно осуществить по отношению к нему мыслительную операцию вычитания из него каких-то признаков, либо же мы можем добавлять ему какие-то признаки, при этом объект будет изменяться. Но если так, то получается, что объект является нам через свои признаки. Объект - это как бы (материальный) носитель признаков, с другой стороны, признак - это некая определенность, некоторая способность, свойство объекта. Т.о. объект и его признак - это противоположные стороны одного и того же. За признаком мы видим объект, объект же заявляет нам о своём существовании через признаки, которыми он обладает. Поэтому в качестве положенной стороны мы можем брать одну либо другую сторону. Это значит, что признак мы можем рассматривать как объект, объект - как совокупность признаков.
А если так, то мы можем о каком-то свойстве объекта говорить как об объекте. Поэтому мы имеем право рассматривать признаки сами по себе как объекты постольку, поскольку в любом случае их реальностью являются последние. В качестве такого объекта будем рассматривать числа. Тогда объекты a1 и т.п. будут выступать для нас в качестве каких-то определенных чисел.
- Законы сложения и умножения (продолжение)
- Пусть есть какие-то числа a1, a2, a3, например, a1=3, a2=2, a3=4.
+, -, *, / - это знаки операторов, то есть знаки, которые предписывают определенные действия. Всякое действие характеризуется направлением; в общем случае идут от чего-то к чему-то и в результате получают что-то. Будем считать, что действия выполняются слева направо. Тогда запись вида a + b предписывает взять объект а и осуществить операцию сложения с объектом b. То есть она предписывает порядок осуществления операции. Будем считать, что операция сложения двух множеств заключается в непрерывном пересчете элементов одного множества и затем второго множества. Например, если мощность mA множества А =3, mB множества В равна 2, то сложение заключается в том, что мы пересчитываем элементы множества А: 1,2,3 и затем продолжаем непрерывный счет, перейдя к пересчёту элементов множества В: 4, 5. Т.о. оказывается, что последнее число, полученное в результате пересчёта, представляет сумму чисел, результат сложения равен 5. Если мы начнём пересчет с элементов множества В: 2+3, то получим тот же результат. В этом заключается закон коммутативности: применение операции сложения к объектам не зависит от их порядка: a+b=b+a
Значительный интерес представляет собой операция вычитания, определенная как противоположная операции сложения, но определенная независимо от неё. Под операцией вычитания следует понимать ввиду обратный счёт, именно, если даны два множества А и В, то А-В определяется как обратный счет элементов А на величину мощности множества элементов В Например, если mA = 3, mВ = 5, то обратный пересчёт даст: 3,2,1,-1,-2. Т.о. в результате вычитания мы получили новое множество с отрицательными элементами. Если же мы будем рассматривать разность В - А, то получим 2. Т.о., при вычитании имеет значение порядок объектов при применении операции, а-b≠b-a; тем не менее, результаты оказываются сопряженными друг с другом, то есть а-b=-(b-a)
Закон ассоциативности выполняется для операции сложения на основании очевидных соображений, закон ассоциативности для вычитания не выполняется. Например, 2-(3-4)=3, (2-3)-4 = -5
Законы коммутативности и дистрибутивности для умножения непосредственно иллюстрируются деревьями рис.1. Закон ассоциативности иллюстрируется рис.2:
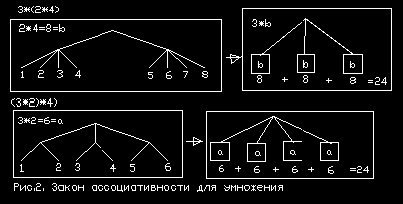пусть a1, a2, a3 равны соответственно 3,2,4, тогда a1* a2*a3 =3*2*4.
Закон ассоциативности гласит, что порядок выполнения операторов умножения (как и сложения) не имеет значения: a1*( a2* a3) = (a1* a2)* a3
В связи с этим отметим, что закон коммутативности говорит, что не имеет значение порядок объектов при выполнении операций сложения и умножения, закон ассоциативности - что не имеет значения порядок выполнения операторов.
Возведение в степень: 23=2*2*2=2+2+2+2. С формальной точки зрения возведение в степень легко приводится к операции сначала умножения, а затем сложения. Однако в самой форме выражения степени видно, что в основании мы имеем дело с одним и тем же множеством, а показатель степени указывает на число сомножителей. То есть сравнительно с умножением мы имеем дополнительное ограничение, заключающееся в том, что при переходе к умножению в качестве сомножителей мы имеем множество копий одного и того же множества элементов.
- Знаки
- умножение плюса на плюс или минуса на минус даёт плюс, умножение минуса на плюс или плюса на минус даёт минус. Возникает справедливый вопрос: почему так? Отвечают: так договорились. А почему договорились именно т.о.? Что мы замечаем в схеме договора? симметрию: одинаковые знаки чисел дают плюс, разные - минус. Что явилось следствием договора? невозможность извлечения корня из отрицательных чисел. Но если существует такая потребность, то она выражает собой отношение симметрии операций возведения в степень числа и извлечения из него корня.
Прежде, чем продолжить, я выскажу одну идею, которую не буду никак обосновывать, но попрошу вас прочитать статью "Числа как операторы" профессора В.А.Брусина. Важным представляется динамический аспект, закладываемый им в понятие числа. Брусин пишет:"
Вернемся к интерпретации чисел как операторов умножения и перенесем ее на комплексные числа.
Каждое комплексное число c будем понимать как оператор, преобразующий радиус-вектор произвольного числа z в радиус-вектор числа cz: z cz. Такое преобразование, исходя из изложенного выше, будет изображаться на комплексной плоскости как некоторая комбинация преобразований растяжения, сжатия, инверсии и поворота. При этом мнимая единица i будет соответствовать оператору поворота радиус-векторов на угол p/2 против часовой стрелки. Это характеристическое свойство можно взять за определение числа i. Это будет определение, из которого исключен всякий мистический смысл. Именно это характеристическое свойство и определяет прикладное значение числа i и комплексных чисел вообще в физике и инженерных науках. "
В связи с идеей рассмотрения чисел как радиус-вектора, можно принять следующие правила относительно знаков:
1. Употребление чисел таково, что числа могут рассматриваться как положительные, отрицательные и не имеющие знака. Последний способ употребления чисел появляется, начиная с операции умножения так, как об этом говорилось выше.
2.При рассмотрении чисел важным является направление вращения представляющего его радиус вектора как положительного либо отрицательного. Тогда знак результата умножения -а*b и a*(-b), то есть минуса на плюс либо плюса на минус будет определяться направлением вращения радиус-вектора в соответствии с договоренностью.
3. произведение минуса на минус всегда даёт минус, произведение плюса на плюс всегда даёт плюс.
Рассмотрим содержательные аспекты употребления знаков, которое, как видно, связано с вопросом о симметрии прямых и обратных операций.
Возьмём декартову систему координат на плоскости. По осям абсцисс и ординат мы имеем дело с числами. Возьмём произведение чисел xi*yj, где 0<i,j<∞ В результате мы получим площадь в первом квадранте в качестве положительной, что справедливо. Возьмём произведение произвольных чисел в третьем квадранте. В результате мы также получим площадь. Но площадь эта лежит целиком в отрицательной области, поэтому она не может быть положительной. Она - отрицательная. Поэтому минус на минус никак не может давать плюс.
Теперь возьмём второй и четвёртый квадранты. Они характеризуются числами с противоположными знаками, в связи с чем возникает вопрос о том, какого рода знак будет носить площадь. Если исходить из статического отношения, то мы не сможем сделать никакого утверждения. Речь должна идти о динамике, о процессе, а именно, об изменении, о направлении приращения чисел. Множество возможных площадей и, соответственно, приращений к ним определяется основанием и аргументом радиус-вектора, причем, очевидно, что соотношение чисел хi, yj обусловливается положением аргумента радиус-вектора, а направление процесса и, соответственно, доминирующей составляющей определяется направлением радиус- вектора точки, представляющей пару чисел. Поэтому здесь должно присутствовать "над" и "под", во-первых, направление процесса, которым показывается доминирующая тенденция, и во вторых, "мера силы" "обороняющейся" стороны. Если формально принять равновесие противоположных сторон как равенство чисел, дающее в качестве площади квадрат, то все остальные площади при постоянном модуле должны рассматриваться по тому, происходит ли приближение к квадрату либо удаление от него. Если приближение к квадрату, то доминирует сторона, имеющая большее число, и, соответственно, площадь имеет знак большего числа, однако, так как движение отрицательное, то само это доминирование является ложным, умирающим. Напротив, если удаление от квадрата, то доминирование является истинным. Соответственно получаем: при движении против часовой стрелки радиус - вектора во втором квадранте мы получаем минус, в третьей квадранте - плюс, если движение радиус вектора по часовой стрелке, то во втором квадранте получаем плюс, в третьем - минус.
Сказанное позволяет определить мнимое число i как равное -1, умножение -1*-1 даёт -1, соответственно, корень из -1 даёт -1. Т.о. мы получаем две качественно противоположные единицы - положительную и отрицательную, то есть своего рода распадение беззнаковой единицы на свои противоположные стороны.
Еще одно замечание по поводу закона знаков. В качестве исходного мы имеем при умножении тиражируемое множество, элементы которого могут быть положительными либо отрицательными. В то же самое время множители-тиражиторы не могут быть ни положительными, ни отрицательными, поскольку ими утверждается лишь количество копий исходного множества, "число раз". Поэтому в результате мы получаем те качественные элементы, которые принадлежат тиражируемому множеству. Поэтому в результате мы получаем либо элемент отрицательные, либо положительные. Например, -3*2 = (-1+-1+-1)+(-1+-1+-1)=-6. В то же самое время выражение вида -3*-3 не принадлежит линейному принципу и должно рассматриваться в другой системе понятий
-
Принцип линейности
- В настоящем разделе будем иметь ввиду ряд натуральных положительных и отрицательных чисел и число ноль. Существо принципа линейности заключается в том, что в результате применения операций мы будем получать объекты того же самого рода, или, иначе, элементы исходных и результирующих множеств будут одни и те же.
- Базовая операция
- В качестве исходной, базовой операции рассматривается операция сложения. (В связи с этим, замечание относительно прямых и обратных операций. Под прямой операцией
понимается операция, которая нечто порождает. Под обратной - операция, которая позволяет от порожденного перейти к первоначальному состоянию. Например, операция вычитания рассматривается в качестве обратной потому, что она имеет дело с порожденным, так как без сложения не может быть вычитания. Хотя, если устранить генетический подход, то с тем же успехом, по-видимому, в качестве прямой операции может быть взято вычитание.)
Ниже операции умножения, деления, возведения в степень и извлечения корня будут выражаться через операцию сложения и обратную ей операцию вычитания.
- Умножение и деление. Линейные единицы измерения и многоразрядное (многоединичное) представление чисел.
-
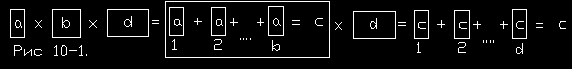Мы уже рассматривали операцию умножения в
соответствующем разделе. Рис. 10-1 иллюстрирует принцип линейности, которым оставляются в стороне содержательные вещи, которые проявляются,
когда умножение иллюстрируется посредством дерева. Замечу, что полезную услугу дерево оказывает нам также и при операциях сложения и вычитания.
Рис. 10-2 иллюстрирует, например, бюджет семьи, который образуется соответствующими взносами её трех членов. Это - сложение.
При этом как отдельный член семьи, так и все члены семьи могут заявить об автономном экономическом существовании, и тогда производится соответствующее вычитание. При этом, однако, следует иметь ввиду, что вычитание совсем не обязательно осуществляется в соответствии с внесенными суммами. В этом последнем случае вычитание уже не является обратной операцией по отношению к сложению в собственном смысле слова. Мы можем представить себе и обратное отношение: существует какая-то сумма, которая разбирается членами. Например, банк, выдающий беспроцентный кредит. В результате этого "банк остался без денег, которые оказались на руках частных лиц". Мы получили в качестве прямой операции вычитание, которому соответствует обратная операция сложения - возврат банку
частными лицами занятых денег.
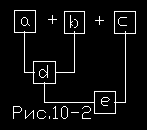Рис 10-1 иллюстрирует операцию умножения, рассматриваемую как тиражирующую исходное множество. Операция умножения - бинарная операция, в которой одно слагаемое принимается за тиражируемое множество, второе слагаемое определяет число тиражируемых множеств. Т.о. операция умножения оказывается выраженной через операцию сложения. Ограничение, которое при этом накладывается на операцию умножения
сравнительно с операцией сложения состоит в том, что при переходе к её выражению через сложение все слагаемые оказываются равны друг другу.
Но если операция умножения выполнима для любых "натуральных множеств", то обратная операция, операция деления этим достоинством не обладает. В этом смысле операция деления является обратной относительно операции умножения, если исходить из принципа, что прямой операция является тогда и только тогда, если она выполняется для любого элемента множества. Результатом деления является множество одинаковых по мощности множеств. Например, 15/5=3. Результат три - это пять множеств по три элемента. В то же самое время 15/4 не имеет решения, так как не существует четырёх множеств с одинаковым числом элементов. Этим недостатком не обладает операция вычитания, так как она допускает вычитание любых натуральных множеств из любых, что достигается благодаря введению отрицательных натуральных чисел: 3-5=-2. Итак, важным является то, что уже операция деления может выступать только в качестве обратной операции. При этом следует обратить внимание вот на что: 15/4=33/4. При делении мы получили остаток 3, который берется в качестве числителя, а в качестве знаменателя берется делитель, который представляет единицу, которая в данном случае равна 4/4. В этом смысле единицу элемента натурального множества мы можем разделить на любое число одинаковых частей, получив при этом производные единицы. Например, 15/7=21/7). Единица - это 7/7. Т.о., в результате деления мы получаем семь натуральных множеств по два элемента, сложение которых даст нам 14, и семь "вырожденных" натуральных множеств, которые в сумме дают единицу. Т.о., мы получаем наряду с единицами также их части, что-то в роде "два землекопа и две трети". Но это говорит о том, что мы должны покинуть реальность "жёстких, заданных объектов и соответствующих им жестких единиц, и перейти к объектам как угодно делимым и поэтому допускающим применение произвольных единиц, и, следовательно, переход от одних единиц измерения к другим. Возьмём отрезок, в котором избранные единицы укладываются 15 раз. Нам нужно этот отрезок разделить на 7 равных частей. Вы обратили внимание, что принцип равенства объектов у нас остаётся. Мы просто предоставили себе определенную свободу в отношении образование из одних единиц других единиц, но от нас требуется, чтобы множества, которые мы получим, содержали в себе единицы, которые укладываются целое число раз в каждом из множеств. Как мы поступаем? Мы умножаем 15 на семь, то есть число объектов на число, на которое мы должны его разделить 15*7=105, и теперь тот же самый отрезок делим не на 15, а на 105 частей. И теперь мы можем спокойно разделить отрезок на семь частей, каждая из которых будет содержать в себе по 15 единиц (объектов). Т.о., мы возвратились от рационального к натуральному множеству чисел с иными единицами измерения.
Т.о. процесс перехода от натуральных к рациональным множествам подчиняется определенным правилам, которые оказываются непосредственно связаны с операцией деления. Натуральные и рациональные числа оказываются привязаны друг к другу.
Значит, каким правилам подчиняется переход от натуральных к рациональным множествам? Во-первых, этот переход связан с потребностью в действии деления множеств. Во-вторых, потребность возникает тогда, когда существующие единицы деления не позволяют разделить объект на множество подмножеств, содержащих целое число этих единиц. Тогда возникает задача перехода к другим единицам, которые удовлетворяли бы этому требованию и в то же самое время были связаны с исходными.
Т.о., то число, на которое делится натуральное множество, становится средством перехода к единицам другого порядка. Что мы получаем? Мы исходную единицу делим на величину делителя. То есть исходной единице 1 мы ставим в соответствие множество единиц, укладывающихся в ней целое число раз. 15=11+12+ ... +115: ; 1i = 1i1 + 1i2+...+1i7 =1ij, 1≤i≤15, 1≤j≤7. Если мы обратимся теперь к дереву, представляющего умножение множеств, то мы увидим подобную же картину принадлежности элементу множества какого-то множества. И в этом смысле мы можем построить ряд принадлежностей единицам единиц. Т.о. если а - какая-то единица, то аi где i-постоянная, может рассматриваться как множество единиц, целое число раз в нём укладывающееся, аij, j- постоянная- единица, укладывающаяся целое число раз в единице аi и т.д. В этом случае выражение вида ааiaij...aij...n представит собой многоразрядное число "с разными основаниями" в разных разрядах. Теперь для того, чтобы перейти к десятичной схеме выражения числа достаточно приравнять все основания деления единиц десяти, так что число 386, 715 представит множество единиц деления, каждая соответствующая определенному разряду: разряд сотен, десятков, единиц, десятых частей единицы, сотых частей единицы, тысячных частей единицы, с их законами связи, выражающихся в перенесении единиц, заимствований единиц из старших разрядов и т.п.
Таким образом операция умножения всегда оставляет нас в сфере натуральных множеств. Операция деления даёт естественный переход от натуральных к рациональным множествам, при этом определение единицы оказывается непосредственно связано с делителем.
- Возведение в степень и корни
-
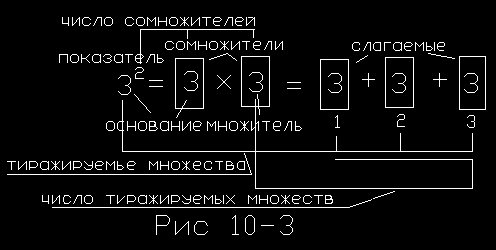
Возведение числа в степень накладывает дополнительные ограничения на умножение: сомножители должны быть равны. Из рис.10-3 видно, что показатель степени указывает на число сомножителей. Если показатель степени равен n, то получаем n сомножителей.
Если an, то при условии, что для всякого i, где i=1,2, ... n, аi = a, степень числа, выраженная через сумму, выглядит так:
an=a1 * a2 * ...* an
a1 * a2 = ∑1<i<aa = a1,2
a1,2 * a3 = ∑1<i<a a1,2= a1,2,3
. . . . . . .
a1,2,...,n-1 * an= ∑1<i<aa1,2,...,n-1 =a1,2,...,n
Любое натуральное число мы можем возвести в любую "натуральную" степень. Но не из каждого натурального числа можно извлечь корень соответствующей степени. Идея решения проблемы заключается в ограничениях, которые накладываются на операции умножения и возведения в степень сравнительно с операцией сложения. Поэтому мной осуществляется опыт перехода от "высших" операций к "низшим". Вообще принцип, который мной закладывается, состоит в поверке "высших", "производных" операций низшими, а в конечном счете лежащими в основании всех операций - в данном случае операции сложения. Вот с этой точки зрения мной и будет рассматриваться понятие корня. Если у нас есть натуральный ряд, то мы моем рассмотреть относительно него то, что называют корнем. Будем рассматривать корень как операцию, обратную операции возведения в степень. Ограничимся вопросом возведения натурального числа в квадрат. Тогда n2=n*n=n1 + n2 +...+ nn, где ni = n, i=1,2,...,n. Так как возведение в степень - прямая операция, то возвести в степень мы можем любое натуральное число, и в этом смысле каждому натуральному числу можем поставить в соответствие его квадрат. При этом можем возникнуть впечатление, что наряду с множеством натуральных чисел мы получаем равносильное с ним множество их квадратов. Но это было бы возможно при условии, что мы создали какой-то новый ряд сущностей. Но следует различать число и то, каким способом оно получено, а точнее, каким способом осуществлен переход от одного числа к другому. Поэтому, конечно, мы продолжаем иметь дело "с одним рядом натуральных чисел", и любые наши операции дают переход от одних чисел к другим, или, соответственно, от одних множеств к другим. Т.о. 12 = 1*1 = 1 (если мы элемент 1 возьмём один раз, то получим один элемент), 22=2*2=2+2=4, 32= 3*3=3+3+3=9 и т.д. Другими словами, дело может быть представлено т.о., что мы, беря какие-то числа и осуществляя какие-то операции над ними, в результате этого получаем какие-то другие числа. Т.о., если нам дано число 1, то 1*2=2, 1+2=3, 22=4, 4+1=5, 3*2=6, 6+1=7, 4*2=8, и т.д. Мы видим, что возведение в степень даёт нам какие-то отдельные, не связанные между собой числа. Теперь если брать извлечение корня как обратную операцию, то мы видим, что она не может быть применена ко всем без исключения числам натурального ряда, и мы можем не знать, возможно ли извлечение корня и какой именно степени из данного нам числа. Если же мы, тем не менее, будем пытаться это делать по отношению ко всем числам, то тем самым мы определим извлечение корня как прямую операцию, и в таком случае нам нужно иметь технологию для извлечения корня, которая должна быть обратной технологии получения степени числа. Если мы знаем, что 4 = 22, то, памятуя, что 22=2*2=2+2, мы, зная, что показатель степени равен двум, должны будем иметь дело с двумя множествами одинаковой мощности, которой определяется число суммируемых одинаковых слагаемых, а в общем случае показатель степени определяет число одинаковых сомножителей произведения, а мощность сомножителей как множеств определяет число слагаемых, которые получаются при каждом применении операции умножения. Благодаря этому мы можем проверить, является ли данное число числом n-ой степени, и только это даёт нам право извлекать из него корень. Например, возьмём число 27 и зададимся вопросом, является ли оно квадратом какого-то числа. Если квадрат, то мы имеем два одинаковых сомножителя. 5*5=25, 6*6=36. Следовательно, х=271/2 не существует. Допустим, показатель степени равен n=3. Тогда имеем три сомножителя одинаковой мощности, и число слагаемых, соответствующих отдельному примененибю операции умножения, должно быть равно мощности множества, представленному сомножителями. Так как степень три предполагает двойное применение операции умножения, и так как порядок применения операций при извлечении корня противоположен порядку выполения степени, то у нас должно быть на первом этапе два сомножителя, один из которых представляет собой сумму со слагаемыми, мощность которых равна мощности второго сомножителя. Допустим, это число 1. Тогда 1*1=1≠27. Допустим, это число 2. Тогда (2+2)*2=8≠27. Пусть корень - число 3. Тогда (3+3+3)*3=27.
Поскольку мы имеем дело с натуральным рядом чисел, нам совершенно ясно, что мы не можем извлекать корни из любых чисел, поскольку корни принадлежать числам, которые получены благодаря операциям сокращения сложения. Ведь действительно, и операция умножения, и операция сложения - это не более как сокращенные способы сложения, которые требуют для своего выполнения дополнительных условий: умножение - предполагает одинаковые слагаемые, и при умножении второй множитель всегда указывает на их число, так же как возведение в степень являет собой сокращение операции умножения, и вводит, соответственно, требование одинаковых по мощности сомножителей. Поэтому если гиперболизировать идею невозможности извлечения корня из множества чисел натурального ряда, то можно считать, что все являются иррациональными, что является, конечно, излишне грубой мистификацией, которая заключается в том, что обратную операцию начинают принимать за прямую.
Но давайте и мы поступим точно таким же образом и выставим требование получения корня из любого натурального числа.
Что такое натуральное число в принципе? Само по себе натуральное число - это далее неделимая единица. Давайте отбросим это требование и скажем, что единица может делиться бесконечно точно также, как и увеличиваться. Но что значит - "бесконечно делиться"? Разве можно актуально представить этого рода бесконечность? А потенциально? Ведь с бесконечностью как таковой в практической жизни человек дела не имеет. Значит, нужен процесс. который позволял бы реализовать любую "бесконечность", то есть иметь возможность бесконечного движения в направлении деления единицы с тем. чтобы это движение было определенным, фиксированным, чтобы мы всегда знали, о чем говорим. Поступим достаточно просто: мы разделим единицу на какое-то число частей, получим новые единицы, от которых мы всегда можем перейти к исходным, затем полученные единицы снова разделим, и этот процесс формирования единиц мы можем продолжать бесконечно. Теперь договоримся об общем основании деления всех единиц, например, равном десяти, и образуем таким образом многоразрядное число, в данном случае нам всем известное десятичное. Т.о. возникает впечатление, что числом представлена многослойная реальность единиц, своего рода система координат, позволяющая определить положение некоей реальной точки в каждом из слоёв-разрядов и тем самым иметь дело с определенным числом. Т.о. мы переходим от натуральных к рациональным числам, в которых связь между соседними разрядами осуществляется на основе приравнивания единицы старшего разряда десяти ( в десятичной системе счисления) младшего. Что в этом случае происходит с проблемой извлечения корня?
Допустим, нам нужно извлечь квадратный корень из 2. Но из 2 корня не может быть, поскольку 2 не получено возведением в степень никакого числа. Единственное, что мы можем сделать, это взять числа, представляющие ближайшие корни, а это 1 и 4, и рассматривать их как приблизительно выражающие корень из двух, единица с недостатком, 4 - с избытком.Что еще мы можем сделать? перейти к единицам меньшего разряда. Тогда 21/2 = (20/10)1/2=201/2 / 101/2Поступаем, как и в предыдущем случае, находя ближайший корень с недостатком для 20 и 10, получаем 4.3 = 1,1(3), возьмём теперь 200/100, получим, соответственно, 14/10=1,4, возьмём 2000/1000=44/31=1,41; т.о. мы получаем приближение к 2: , (20/10)2 = 1,1(3), 200/100 = 1,4, 2000/1000 = 1,41, где 1,412 = 1,9881, что уже совсем близко к двум. Что всё это значит? это значит, что число 1, 9881 имеет корень, а число 2 корня не имеет и неоткуда ему взяться. Но 1,9881, конечно, отличается от натурального числа.
Возьмём натуральный ряд чисел, и сделаем уточнение: в качестве единиц берем не отдельные неделимые объекты, а метрические, и в этом смысле натуральный ряд чисел можно назвать метрическим. Что лежит в его основании? какая-то величина, которая принимается нами за единицу, например, какой-то отрезок на линии. Из этого отрезка мы формируем натуральный ряд чисел. Теперь обратим внимание вот на что: из какого-то числа отрезков мы можем сформировать производную единицу, мы можем определить правила, по которым будем формировать производные единицы. Например, десять единиц можно рассматривать как производную относительно избранной единицы, десять единиц производной единицы в свою очередь можем рассматривать в качестве единицы и т.д. С другой стороны, избранную единицу мы можем точно также бесконечно делить на более мелкие единицы в соответствии с тем же правилом десятков. В результате мы получим многоразрядное число в основании которого лежит избранный нами масштаб, которое представлено бесконечным множеством взаимосвязанных единиц. Т.о. мы перешли к конструкции действительных чисел - рациональных и иррациональных, причем, на деле за термином "иррациональные числа" нет никакой мистики, поскольку это всего лишь числа, которые не получены посредством операции возведения в степень.
Возвратимся к вычислению корня из двух. Если натуральный ряд чисел, то мы от единицы переходим к двум. Этими переходами определяется шаг дискретности. Если мы берем десятые части единицы, то процесс качественно изменяется: если представить себе движущуюся точку, то она должна пройти 1/10, затем вторую десятую, добраться до 10/10, и только теперь мы получаем единицу, которая оказывается суммой её десятых долей. Дальнейшее движение точки даёт 1.1, 1.2 и т.д. Поэтому теперь в качестве того, какое число может рассматриваться в качестве корня 2, мы можем выбирать из множества промежуточных значений между 2 и 1. Памятуя, что за понятием "корень" стоит произведение двух одинаковых сомножителей, мы можем делить число 2 на числа т.о., чтобы в результате было получено максимальное приближение к их равенству. Например, 2/1=2, 1 меньше2, поэтому делитель должен быть увеличен. 2/1,5=1,(3), частное меньше делителя, делитель нужно уменьшать: 2/1.4=1.4. 1,42=1,96. Если мы хотим получить большую степень приближения, мы должны ввести следующую производную единицу, разделив предшествующую на 10, и тогда отдельный шаг станет равным сотой части исходной единицы, и мы 2 можем делить теперь на 1,41 и т.д.
- Добавление (вставка)
- Пусть мы имеем натуральный ряд чисел N.
Если мы попытаемся рассматривать его с точки зрения принципа равномерности, то должны будем признать, что этот принцип им выполняется.
Мы имеем дело со своеобразным дискретно-непрерывным процессом, в котором
каждое следующее число даёт то же самое приращение. Ведь отдельная единица
может быть представлена в качестве отрезка какой-то величины, и поэтому
расстояние между двумя любыми единицами одно и то же, а именно этот признак
нами кладется в понятие равномерности. Хотя, разумеется, если представим
точку, которая движется по натуральному лучу, то её движение может быть
неравномерным, так что частота, с которой она будет проходить единицы, будет
различной, и тогда расстояние для этой точки с точки зрения одного и того же
времени будет то сжиматься, то расширяться. Это - если мы расстояние
измеряем посредством времени. С другой стороны, в случае движущейся
точки мы можем измерять время посредством расстояний, и тогда мы получим
переменное время. Т.о. пространство и время оказываются мерами ("мерилами") друг друга,
где под мерой понимается, сколько чего-то в чём-то. Понятно, что понятие
меры возникает только там, где есть движение.
Соответственно, натуральный ряд чисел N может рассматриваться как актуальная либо потенциальная бесконечность. Понятие актуальной бесконечности предполагает построенную, актуально существующую бесконечность. Понятие потенциальной бесконечности предполагает процесс её построения. Хотя в последнем случае процесс построения бесконечности можно рассматривать как протекающий во времени, и мы имеем дело с движением, однако это "не то движение". Это подобно тому, что мы строим дорогу. Разумеется, её строительство происходит с какой-то скоростью. Но это, конечно, не движение автомобилей по дороге относительно километровых столбов, отсчитывающее натуральный ряд чисел.
Если теперь мы представим себе, что операции приращения занимают одно и то же время независимо от величины отрезков приращений, то если мы исходную единицу разделим на а частей, то процесс равномерного построения потенциальной бесконечности перестанет быть равномерным. При всей кажущейся натянутости такого допущения в приложении к практике именно оно имеет место, поскольку, к примеру, разные участки дороги в соответствии с ландшафтом местности и особенностей грунта строются в течение разных интервалов времени, а это как раз и означает деление исходной единицы на части и, соответственно, неравномерность. Значит, во-первых, в любом случае за понятием равномерности незримо стоит время, и неравномерность выражается в применении разных единиц измерения. Т.о., для натурального ряда чисел неравномерность выражается в применении разных единиц измерения. Синтез их реализуется рациональным рядом чисел R