на главную страницу
визитка
назад
назад карта
Утро. Звонит будильник. Обычно по звонку Виталя бодро подскакивает, включает
музыку, за ним подтягиваюсь я, и мы начинаем делать зарядку. Сегодня он
лежит неподвижно и важно. «Тише – говорит он – меня посетила гениальная
идея. Всю ночь снилась»
«Видишь ли, я стараюсь разобраться – продолжает он через время- Возьми две
прямые, пересекающиеся под прямым углом. Вот тебе система координат, назовём
её Ψ.»- И вдруг он смеется, глядя на меня: «Всех понимать»- говорит он,
словно кого-то передразнивая. Очевидно, ему в голову пришла
новая мысль,
вследствие которой он поворачивается на бок и
подпирает голову согнутой в локте рукой. Он смотрит на меня так, как будто
впервые видит: «Говоришь, всех понимать?» Я с недоумением смотрю на него. «Я
имею ввиду, что ты из тех, кто стремится всех понимать. И от этого понимания
еще и чувствовать себя обязанным «входить в чужое положение». А если не
понимать? Смотри, пожалеешь!» - говорит удовлетворенно Виталя и его тело
принимает первоначальное положение. «А я думаю, чего это мне не хватает. Всё
лишние части в схеме появлялись, не знал, куда их приткнуть.» - его мысль
пробирается неведомыми мне тропами.
-Так что у тебя за идея?
- Обозначь прямые как «а» и «в», точку пересечения – О, лучи прямой «а» как
ОА, ОВ, прямой «в» OC, OD т.о., что по часовой стрелке они располагаются в
последовательности ОА, ОС, ОВ, OD. Возьми произвольную точку Е между лучами
ОА, ОС, опусти перпендикуляры на эти лучи, получишь отрезок ЕF с точкой F на
луче ОА, и отрезок ЕG с точкой G на луче ОС. Ты определил положение точки Е
относительно системы координат Ψ. Теперь начни изменять величину угла между
лучами а,в. Само это изменение можно рассматривать как процесс,
как функцию от времени. В результате этого для
всякого момента времени мы между лучами ОА, ОС будем иметь какой-то угол α.
Точка Е в исходном положении представляла собой
вершину прямоугольника ЕFОG. Представь себе, что точка Е прямоугольника
жестко-шарнирно связана с образующими его отрезками. Тогда с изменением
значения угла АОС точка Е начнет изменять свое пространственное положение, и
прямоугольник преобразуется в параллелограмм.
Т.о. мы получаем правило определения положения точки в системе координат
с произвольным углом в первом квадранте, согласно которому линия,
соединяющая точку с лучом, должна быть параллельна противоположному лучу.
Значит, если система координат образована двумя пересекающимися прямыми, угол
между двумя лучами
АО и ОС =АОС, то если в ней дана точка, то для определения положения
её в системе координат, необходимо провести прямые, параллельные этим лучам,
до пересечения их с противоположным лучом.
При этом, конечно, возникает вопрос о переходе от системы координат с углом
α между прямыми в первом квадранте к системе координат с углом β в первом
квадранте, но вычисление этого – дело техники» - сказал Виталя и замолчал.
Я решил, что этим его гениальная идея исчерпала себя, и заметил: «А всё –
таки!» «Отвлекаешь ты меня – досадливо сказал Виталя. -Это уже мелочи.» «Ну,
да, гладко было на бумаге.» Виталя рассердился, и настолько, что встал с
постели и подошел к столу.
«Вопрос стоит так: если дана прямоугольная
система координат с точкой Е в ней, то, конечно, существенно, как изменяется
угол α, потому что это связано с вращением лучей, а они могут изменять свое
положение одновременно. Но допустим, что вращается вокруг точки О только
прямая а. Тогда для любого фиксированного значения α мы, в соответствии с
построением, можем определить положение точки в
текущей системе координат . Задача, следовательно, состоит в том, чтобы,
зная значение положения точки Е для одного значения
α, определить её значение для другого значения α. Дано: GE=OF; EF=OG; углы
GOA, HOA. Найти НЕ Угол GOH = разности углов GOA и HOA. Синус угла GOH = GH
/ OG, откуда GH = произведению GH на синус угла GOH. Отсюда НЕ =GE – GH или
OF = произведению ОG и синуса разности углов GOA и HOA Подобным же образом
находишь ОН.» Виталик даже не поленился и сделал рисунки.
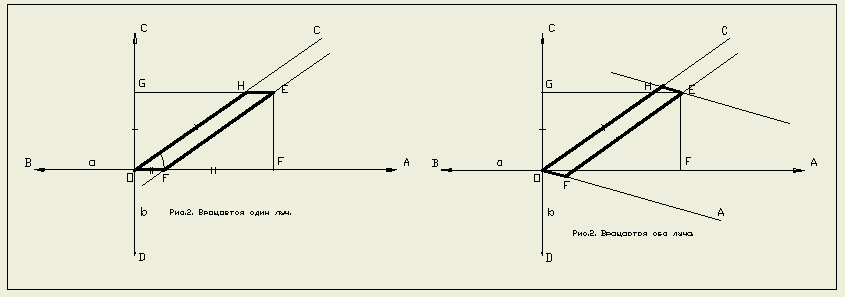
-Но в общем случае мы не будем иметь прямоугольных координат, а вращаться
могут оба луча.
Тогда с лучом, принимаемым за абсциссу, мы можем
совместить дополнительно абсциссу прямоугольной системы координат, а
изменение углов вращения можем рассматривать как суммарное от движения обоих
лучей. Словом, эта проблема решаема.»
-Всё? –спросил я у Виталика.
-Нет. – возразил Виталик – ты знаешь, что мне приснилось? Угол. Угол
пространственной системы координат, причем, не обязательно прямоугольной, и
моё второе я сказало мне, что это важно. Я, конечно, чувствую, что это
важно, что в этом что-то есть, но что именно, понять не могу. Во сне я
спросил, в чем может быть важность такого угла. «Возьми две пересекающиеся
плоскости – сказало мне моё второе я – Что ты видишь?» «Они пересекаются по
прямой. Ну, и что?» - « А то, что есть одна плоскость, на ней может быть
образована бинарная система координат. Если перпендикулярно пересекаются три
плоскости, то на них может быть сформирована пространственная система
координат. А если две плоскости пересекаются, то линия, по которой они
пересекаются, как будто просит, чтобы через её точки было проведено
множество плоскостей. Получается так, что пересечение двух плоскостей дает
линию, и эта линия как раз и оказывается существенной. Теперь представь
себе, что ты как бы смотришь на пересекающиеся плоскости фронтально, так что
линия
их пересечения представляется точкой. Тогда от точки пересечения
плоскостей, которую ты можешь принять за нулевую, ты влево и вправо, вверх и
вниз можешь отложить числа, и через них будешь определять точки. Но что ты
при этом опять получаешь? Например, пусть одна плоскость расположена
вертикально, другая – горизонтально и допустим, что на горизонтально
расположенной плоскости ты берешь точку. В таком случае эта точка
представляет всё множество точек по прямой, параллельной точке пересечения,
то есть представляет собой линию. Теперь представим себе, что мы передвигаем
вертикальную плоскость. В таком случае мы можем совместить её с этой линией.
Так как точек и соответствующих линий бесконечное множество, то мы можем с
бесконечным множеством линий совместить бесконечное множество вертикальных
плоскостей. Или можем поступить обратным образом и набить вертикальную
плоскость бесконечным числом горизонтальных. Если
бы мы поставили, т.ск., сбоку движок, то, двигая
движок горизонтальной плоскости, мы могли бы находить соответствующую его
значению вертикальную плоскость, а двигая движок вертикальной плоскости, мы
могли бы находить соответствующую его значению горизонтальную плоскость.
Затем, двигая произвольную вертикальную плоскость вверх – вниз, мы могли бы
пересчитывать все соответствующие наборы точек - линий, принадлежащих
плоскости.
Значит, есть бесконечные множества двух пачек параллельных
плоскостей, пересекающихся под каким-то углом. И в каждой из пачек мы
выделяем по плоскости, и
положение всех остальных плоскостей рассматриваем по отношению к
выделенным.
Пересечение двух плоскостей позволяет нам, фиксируя числовое значение
точек-линий одной плоскости, определять другую плоскость. Перемещая другую,
определять множество принадлежащих ей точек-линий. Например, мы поставили
движок горизонтальной плоскости на 10, вертикальной - на 15. Это значит, что
мы тем самым выделили 10 вертикальную плоскость, и на ней выделили 15 линию.
Или обратно: мы выделили 15 горизонтальную плоскость и 10 линию на ней.
-Что ты мне морочаешь голову – спросил я – просто линия перечесения двух
плоскостей определяет множество принадлежащих им обоим точек.
- Разве я о плоскостях говорю? – важно сказал Виталик. – Теперь нам остаётся
ввести третью плоскость…
-Ну, понятно, сказал я – ввести третью плоскость перпендикулярно первым
двум, и, набив в очередной раз этими плоскостями линию, мы сможем определить
любую точку пространства, двигая еще и третий движок, который, установив на
значение 20, мы определим 20 точку пятнадцатой линии десятой вертикальной
плоскости. Ты сегодня думаешь вставать, или нет?
-Еще не всё. Самое важное. Пусть есть система координат на плоскости. Её
можно представить как два входа и два выхода: первый квадрант- ОА, ОС -
входы, ОВ, ОD выходы. Но ведь вторые половины лучей из точки О не
обязательно должны быть продолжением первых. Они могут в свою очередь
вращаться относительно точки О в ту или другую сторону. Причем, их
отклонение может быть функцией от отклонения первых и если в обратном
направлении, то мы получаем возможность представления реципрокной работы
мышц.- победно заключает Виталя.
-М-да - говорю я -Всё, проснулся?
-Ага, врубай музыку!
06.09.07 г.