Заметки по философии логики. Статья 7.
Примечание 1. а) Дискретные события как основание логики. б) Дискретация
непрерывных событий
Примечание 2. Структура, факт,
время выполнения события или его шага, цепочки событий и их запись, импульсные и
постоянные причины.
Примечание 3. Высказывание и его верификации.
Примечание 4. Аксиома независимости. Отношение образа и
прообраза.
Примечание 5. Главный знак высказывания.
Примечание 6. Синонимы
Примечание
1
Не формальная логика лежит в основании дискретных
событий, а отношения между событиями лежат в основании формальной логики. Под
операцией дискретации понимается преобразование непрерывных событий в
дискретные.
Примечание 2.
Под структурой
понимаются связи между событиями. Под фактами понимаются события. Любая теорема
представляет собой формулу, которая состоит из структуры (событий) и
последовательности фактов, возбуждаемых последовательностью реализации событий.
Структура событий - это то, что задано (существует) актуально. Но сами по себе
события разворачиваются потенциально, во времени. Вырожденная форма времени
представляет собой последовательность фактов. При этом модель соответствующего
процесса может быть двоякой. 1. Происходит и исчезает некоторый факт. Тогда если
структура А→В, и факт А, то он возбуждает факт В, т.ск., переходит, превращается
в факт В, при этом сам исчезает.
Если зададим интервал
времени, в течение которого совершается переход, и зададим счетчик, которым
подсчитываются шаги, то если один шаг занимает 1 час, то если А→В, В→С,
С→D - структура, и А - факт, то получим t1=0=A, t2=B, t3=C, t4=D, тогда мы
получаем процесс длительностью в 3 часа. Последовательности типа А→В, В→С и т.д.
могут быть сокращенно записаны в виде А→В→С→...
2. Следствие существует до тех пор, пока существует
причина. Это значит, что если А→В, А, то В будет существовать ровно до тех пор,
пока существует его причина, А. Тогда цепочка связей будет накапливать причины.
соответствующих фактов.
Примечание 3.
Высказывание является переменной до тех пор,
пока оно не верифицировано. Когда говорят, что А, В, и т.д. - переменные
высказываний, то они означают совсем не то, что областью их значения является
множество каких-то определенных содержательных высказываний, а то, что они
обозначают определенные в содержательном отношении высказывания, которые не
верифицированы. Верификация высказывания, если она, опять-таки, возможна,
превращает высказывание из переменной в константу "истина" или "ложь".
Наложение карты высказываний на карту событий
обеспечивает верификацию высказываний.
Примечание 4.
Пусть какое-то положение истинно т.о., что оно истинно независимо от того,
является истинным или ложным какое-то другое положение контекста, в который оно
входит. Если положение А истинно само по себе (является причиной самого себя),
что может быть выражено как А →A, или А=А, то мы можем записать: (А=А)
→(Вv-B→.А=А). Это выражение может быть названо аксиомой независимости. Когда мы
рассматриваем какое бы то ни было положение, мы можем не знать, является оно
зависимым или независимым от других положений. Как мы можем установить его
зависимость или независимость от других положений? Мы должны взять их с
отрицанием. Если их отрицание никак не отражается на нашем положении, то можем
сказать, что оно не зависит от них.
Природные неживые
объекты не обладают сознанием и, соответственно, сознаваемым отражением среды,
то есть у них не происходит удвоения объекта и его отражения (объекту не
ставится в соответствие его отражение). Соответствие объекта и его отражения в
логике выступает в виде закона тождества А=А, и истинное высказывание выражает
это соответствие.
Имея дело с тождеством, мы либо идем от
прообраза к образу, либо от образа к прообразу, и поэтому закон тождества
включает в себя эти два противоположные отношения, что выражается оператором
эквивалентности.
Примечание 5.
Главным знаком выражения называется знак, делящий выражение на две части. Всякая
теорема в качестве главного знака имеет импликацию или эквивалентность, которая
распадается на прямую и обратную импликации.
Примечание 6. Синонимы:
предложение, высказывание,
формула, событие;
теорема, тождественно-истинное
высказывание;
противоречие, тождественно-ложное
высказывание
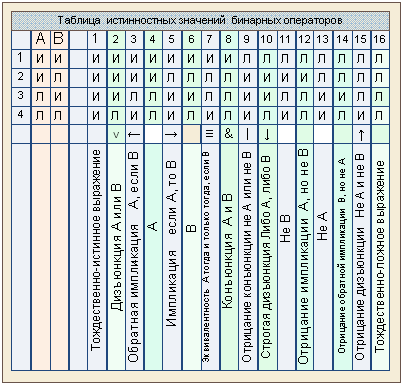
Запишем
закон тождества А→А (1). Подставим на место А/А→В,
получим А→В→.А→В (2). Применим к полученному выражению теорему дедукции,
получим А→В, А
Ⱶ
В.
Получили правило вывода модус поненс, где часть А→В
соответствует структуре (реальности), А - факту, В - следствию из факта.
Сделаем подстановку во (2) А/-А, получим -А→В→.-А→В.
Сократим выражение -А→В, записав его в виде А v B и
станем читать его как "А или В". Тогда две записи -А→В и АvВ
будут обозначать одно и то же, и мы можем записать АvB→.-A→B
Откуда АvB, -A
Ⱶ B Проделаем еще один опыт
относительно (1), подставив на место А/-(А→-В), получим -(А→-В)→-(А→-В). Введем
сокращение записи, приняв, что -(А→-В)= А&B и выражение А&B будем читать как А и
В. Два эти высказывания, звучащие различно и имеющие различный смысле, тем не
менее, говорят разными способами об одном и том же. В одном случае мы говорим,
что А и В истинны, в другом случае говорим, что неверно, что если истинно А, то
не истинно В. Другими словами, одно и то же содержание может выражаться
различно: А&;B
→-(A→-B)&-(B→-A).
При этом следует говорить об эквивалентности явных и неявных определений. А&В
- явное определение. -(А→-В) - неявное определение, так как из того, что если
неверно, что если А, то -В, следует, что если А, то В, так как третьего
состояния для В не дано. Все выводы делаются именно на основе закона
исключенного третьего. В силу симметричности конъюнкции сказать
-(А→-В) или сказать -(В→-А) - значит сказать одно и то же, что позволяет свести
два закона для симметричных операторов к одному закону, и именно потому, что из
-(А→-В) следует -(В→-А) и обратно, так как А→-В ~ B→-A
является тождественно истинным высказыванием и, соответственно, отрицание
импликаций также даёт тождественно-истинное высказывание.
Другими словами, если две импликации имеют одинаковые наборы истинностных
значений и, следовательно, образованная из них эквивалентность образует
тождественно-истинное высказывание, то их отрицание также породит всюду
истинную эквивалентность, то есть снова даст тождественно-истинное высказывание.
Но импликация есть оператор с тремя истинностыми значениями "истина", а его
отрицание порождает оператор с одним истинностным значением "истина". Отсюда
получаем, что если эквивалентность двух импликаций порождает
тождественно-истинное высказывание, то тождественно-истинной будет и
эквивалентность их отрицаний. Значит, любая теорема, части которой, полученные
разделением её главным оператором, имеют одинаковые наборы истинностных
значений, снова породит теорему, если эти её части взять с отрицанием.
Например, А˅(B&C)~(A˅B)&(A˅C).
Взяв отрицание частей, на которые распадается эквивалентность, снова получим
теорему -А&(-B˅-C)~(-A˅-B)&(-A˅-C).
Осуществив подстановки на место отрицаний переменных самих переменных, получим А&(B˅C)~(A˅B)&(A˅C)
Это означает, что множеству теорем, образованных
эквивалентными друг другу высказываниями, соответствует множество теорем,
образованных
отрицаниями этих высказываний. В целом этим обеспечивается переход от операторов
с тремя истинностными значениями к операторам с одним истинностным значением,
как и обратно, переход от операторов с одним истинностным значением к операторам
с тремя истинностными значениямии
Импликация - не симметричный оператор в отличие от антиконъюнкции и
дизъюнкции. Свойство симметричных операторов выражается в симметричности
правил удаления операторов. Именно, если х=А либо В, соответственно у= В или А,
то А˅В, -х
Ⱶ у, и А|B, x Ⱶ -y .
То
есть правила практически одинаковы, и их различие сводится к применению в
качестве посылок разных переменных. Несимметричные операторы (прямая и обратная
импликации) характеризуются "прямым" и "обратным" правилами вывода: А→В→.А→В,
А→В→.-В→-А.
Связь между законом тождества и табличными определениями операторов заключается
в том, что в части, на которые делится выражение закона тождества, могут
подставляться эквивалентные им выражения, то есть выражения, содержащие
одинаковые с ними значения истины. А→В→.А→В. А→В/-В→-А, получаем
А→В→.-В→-А, откуда правило модус толленс А→В,-В
Ⱶ
-А
А дальше возникает вопрос о
выражении операторов через какой - то один, и для этой цели применяется импликация.
Определения операторов различаются тем, что в них в качестве истинных
рассматриваются различные наборы истинностных значений переменных, а это
достигается интерпретации переменных в качестве истинных, если к ним не
применяется отрицание, и в качестве ложных, если применяется. Поэтому
обозначение переменной А имеет ввиду, что А истинно, и значение переменной -А
означает, что А ложно, как и обратно. Поэтому, придавая переменным в импликации
возможные значения, мы будем получать определения операторов, и применение,
соответственно, операции отрицания к оператору, получим противоположный
оператор. Значит, если мы хотим через импликацию выразить другие операторы, мы
должны придавать возможные значения переменным. импликация: Получаем наборы А,В,
-А,В, А,-В, -А,В. Набор А,В соответствует импликации, набор -А,В соответствует
дизъюнкции, набор А,-В соответствует отрицанию конъюнкции, набор -А,-В -
обратной импликации. Этим исчерпываются операторы с тремя истинностными
значениями "истина" Отрицание этих операторов даст, соответственно, операторы с
одним истинностным значением истина, , которые обычно выражаеются через
конъюнкцию, именно, А,В соответствуют непосредственно выражению конъюнкции, -А,В
- отрицанию обратной импликации, А,-В отрицанию импликации, -А,-В - отрицанию
дизъюнкции. В этом смысле можно говорить о двух выделенных операторах -
конъюнкции для выражения операторов с одним истинностным значением
"истина" и импликация, которая применяется в качестве средства, при посредстве
которого строются правила следования.
Мы с вами можем
заметить, что правила, в которых фиксируется независимость одной переменной от
другой, а это операторы 4, 6, 11, 13 таблицы, обладают смыслом, который говорит
о независимости переменной от другой. В доказательствах на практике они не
применяются. Операторы 1, 16 , получаемые один из другого
отрицанием, используются для определения тождественно истинных или тождественно
ложных высказываний. Они являются основанием для подстановки вместо друг друга
эквивалентных частей высказываний. Например, в теорему A→.B→A
на место B→A могут
подставляться эквивалентные высказывания -В˅А, либо
-(А&-B), и мы получим теоремы А→.-В˅А
либо А→.-(А&-B). Всюду речь идет об одном и том
же, но различными способами.
Сам по себе оператор импликации не способен отражать симметрию
непосредственно, но лишь - опосредованно, на основе применения закона коммутации
к симметричным операторам. Например, А→А,
подстановка А/-А→В. -А→В→.-А→В.
А˅В→-А→В. Соответственно, А→А,
А/-В→А, -В→А.→-В→А, В˅А→.-В→А.
Справедливость этих двух
формул имманентно содержит в себе правило коммутативности для дизъюнкции.
Поэтому можем записать формулу также и в виде В˅А→.-А→В.
Аналогично для антиконъюкции:
A-&B→A→-B
и А-&В→.А→-В Однако для обратной импликации
положение вещей изменяется, так как обратная импликация не является симметричным
оператором. А→А, А/-А→-В
-А→-В→.-А→-В А ←В →.-А→-В.
Так как -А→-В ~ B→A, то получаем также А ←В→.В→А
Явно выраженные правила вывода А ← В, -А, В
Ⱶ -В, А
Во всём этом необходимо иметь содержательное рассуждение, так как мы
начинаем понимать формальное тогда, когда оно оказывается связано с нашим
инстинктом, то есть находит своё соответствие в бессознательном. Что оно собой
представляет? То, что оно нечто предполагает какие-то посылки, из которых
делаются выводы. Например, дизъюнкция звучит как А или В, то есть определение
дизъюнкции звучит так, что происходит А, или происходит В, или они происходят
вместе. То есть дизъюнкция истинна, если истинна по крайней мере одна из
переменных. Применительно к таблице истинности определение дизъюнкции указывает
на 1-3 её строки, которые порождают значение истины для дизъюнкции. И,
соответственно, неявно указывается 4 строка, которая порождает для дизъюнкции
значение ложь. Если мы будем иметь ввиду это определение в качестве предпосылки,
то можем сказать, что если -А→В и, соответственно, -В→А, и вывод этот сделан на
основании содержательного определения оператора дизъюнкции. Тем самым -А→ В и
-В→А сами по себе не исчерпывают определения дизъюнкции. Однако, в качестве
симметричных, они говорят об одном и том же, что выражается в одинаковости
таблиц истинности, соответствующих дизъюнкции. -А→В и -В→А - это эквивалентные
высказывания, что становится возможно благодаря тому, что ими описывается
симметричный оператор.
C другой стороны, как мы можем
ставить вопрос? Пусть истинно -А→В и -В→А.
Можем поставить вопрос: относительно отношений каких событий (соответственно,
выражающих их отношения операторов) оно является истинным. То есть если мы
рассматриваем приведенные высказывания в качестве опыта, то какого рода
структура за ними стоит? Из того, что отсутствует А, необходимо следует В. То
есть признак -А указывает на наличие признака В, признак -В указывает на наличие
признака А. Следовательно, здесь говорится, что отсутствие признака одного
события говорит о наличии признаков другого, и обратно. Но при этом не говорится
об влиянии положительного признака одного события на другой, Поэтому эту сторону
дела мы должны исключить. В целом на чем должно основываться здесь рассуждение:
на допущении и не допущении чего-то. Именно, -А не допускает -В, -В не допускает
-А, следовательно, невозможно, чтобы одновременно были события -А, -В.
Применительно к такой категории, как событие "вообще" его единственным признаком
является его существование либо не существование. Никакими другими признаками
оно не обладает, что при перенесении на категорию истины имеет ввиду отношение
соответствия или не соответствия. При этом когда говорится о соответствии, то
под ним понимается не тождество, а связь, или специальное отношение между
различными. Тогда как применительно к одному и тому же речь идет о соответствии
понимаемом в смысле тождества. Но А допускает В, поскольку не говорится о
противном, и В допускает А. Отсюда получаем, что речь идет о событиях, таких,
что они могут сосуществовать, может существовать одно без другого, но они не
могут оба не существовать. А это - отношение, которое выражается оператором
дизъюнкции.
Итак, нами найден способ рассуждения, на
основании которого мы можем перейти от полного описания возможных отношений
между событиями к операторам, выражающим эти отношения.
Т.о., мы получаем возможность перехода от опыта отношений между событиями
определенного рода к выражению отношений между ними. Именно, мы начинаем с
осуществления опытов. то, что мы можем сделать при рассмотрении событий, это
установить формы их совместимости и несовместимости, если рассматривать при этом
в качестве форм событий как их существование, так и их не существование, то есть
событием является как его существование, так и его не существование относительно
к воспринимающему их субъекту, ибо сам обозначение самого факта существования и
не существования чего бы то ни было возможно только при наличии субъекта, это
отмечающего. Поэтому необходимо мы имеем эти две стороны, это тождество
противоположности объекта и его отражения субъектом. И закон тождества отражает
единственно факт адекватного отражения объекта в субъекте точно также , как
-(А~A) выражает отсутствие такого отражения. Поэтому мы и должны разделять то,
что принадлежит реальности и то, принадлежит отражению её в субъекте.
Будем называть состояния события А и -А его модусами. Наши испытания
отношений двух событий заключаются в том, что, вызывая один модус события мы
следим, влияет ли он, и если влияет, то каким образом, на другое событие.
Поэтому, имея дело с двумя событиями А и В, мы должны брать последовательно
модусы А, -А, В, -В и отмечать, как они отражаются, если отражаются, на модусе
другого события.
Рассмотрим еще пример. Пусть А→-В, В→-А Из
существования события А следует событие -В, из существования события В следует
событие -А. Так как описываются все влияния, то отсюда следует, что события -А,
-В не влияют на модус противоположного события, то есть допускаются события -А,
-В. Но наличие события А не допускает события В, как и В не допускает
события А. То есть эти два события не могут сосуществовать. А это соответствует
оператору отрицания конъюнкции.
Как формально можно определить, выражаются ли отношения между событиями
симметричными или не симметричными операторами? Событие без определения его
модуса обозначается заглавными буквами
латинского алфавита, например, А. Если событие А существует, то оно
обозначается как +А или сокращенно как А; если оно не существует, то
обозначается как -А.
Оператор ∆ является симметричным тогда и только тогда, когда
противоположны модусы событий
и описание события представляется тождественно-истинным выражением
вида А∆В=А→-В ~ В→-А, где А
употреблено в метасмысле, то есть в смысле события вообще без указания его
модуса, -А - модус, противоположный модусу А.
Если модусы событий
одинаковы, то мы имеем дело с несимметричным оператором. К несимметричным
относятся операторы прямой и обратной импликации, и выражающая их всегда
истинная эквивалентность имеет вид: А∆В=А→В ~ -B→-A
1. Закон тождества есть эквивалентность и должен поэтому
рассматриваться в обе стороны. Это значит, что если мы з
1. Импликация - не симметричный оператор в отличие от
антиконъюнкции и дизъюнкции. Сам по себе он не способен отражать симметрию
непосредственно, но лишь опосредованно, на основе применения закона коммутации к
симметричным операторам. Например, подстановка на место А в А→А
-А→В, которому соответствует таблица истинности дизъюнкции. Отсюда получаем
А˅В→.-А→В. Соответственно, В˅А→.-В→А. Для дизъюнкции нам потребовалось два
импликативных выражения для того, чтобы исчерпать правила вывода дизъюнкции.
Аналогично для антиконъкции: A-&B→-A→-B и B-&A→.B→-A. И, соответственно, для
обратной импликации А ←В→.-А→-В.
2. Конъюнкция - это оператор с одним истинностным
значением истина. Импликация же применяется только лишь к неоднозначным
операторам, то есть к операторам, которые в правилах удаления требуют для себя,
наряду с оператором, также и соответствующего значения одной из переменных.
Тогда как для однозначных операторов достаточно операторного выражения. А&B→A,
A&B→B.
3. Во всём этом необходимо содержательное рассуждение,
которого у меня до сих пор не получалось. Что оно собой представляет? То, что
оно предполагает какие-то посылки, из которых делаются выводы. Например,
дизъюнкция звучит как А или В, то есть определение дизъюнкции звучит так, что
происходит А, или происходит В, или они происходят вместе. То есть дизъюнкция
истинна, если истинна по крайней мере одна из переменных. Применительно к
таблице истинности определение дизъюнкции указывает на 1-3 её строки, которые
порождают значение истины для дизъюнкции. И, соответственно, неявно указывается
4 строка, которая порождает для дизъюнкции значение ложь. Если мы будем иметь
ввиду это определение в качестве предпосылки, то можем сказать, что если -А→В и,
соответственно, -В→А, и вывод этот сделан на основании содержательного
определения оператора дизъюнкции. Тем самым -А→ В или -В→А сами по себе по
отдельности не исчерпывают определения дизъюнкции. Однако, в качестве
симметричных, они говорят об одном и том же, что выражается в одинаковости
таблиц истинности, соответствующих двум правилам удаления для дизъюнкции. -А→В и
-В→А - это эквивалентные высказывания, что является следствием свойств
симметричного оператора. Будем мы идти справа налево или слева
направо, со структурной стороны правило вывода будет тем же: А˅В,
-АⱵВ
или А˅В,
-ВⱵА.
4. В чем здесь особенность? В том, что мы получаем две одинаковые
истинностные таблицы, и, т.о., объединение этих таблиц знаком эквивалентности
порождает тождественно истинное высказывание.
5. С содержательной точки зрения А и В представляют собой
просто события, без дальнейших признаков, или просто высказывания, выражающие
события, без всякой дальнейшей их конкретизации. И поэтому единственным
свойством этих событий является то, что они разные, но и не более того. Другими
словами, не учитывается порядок событий. А или В - это не события слева направо
(или справа налево). Порядок событий не играет роли. Посылка А˅В - это то, что
относится к структуре, которая перерабатывает два события
т.о., что если не имеет
места одно из событий, то имеет место другое.
6. Однако, преобразованное импликацией в
последовательность, оно уже перерабатывает одни события в другие. Отсюда
получаем: если мы исходим из закона тождества, то им предполагается предпосылка.
в виде таблично представленного определения оператора.
7. Для импликации имеет значение порядок элементов. В
симметричных операторах благодаря выполнению ими закона коммутативности,
мы можем произвольно писать, например,
А˅В или B˅A.
8. Мы должны принять что-то в качестве критерия,
обеспечивающего понимание множества форма импликации.
А этому служит истинностная таблица
бинарных операторов.
1. Любую теорему можно рассматривать в качестве
полученной в результате
подстановок в закон тождества.
2. Например, если А,
то В, то если А, то В.
Где "Если
А то В"- структура, В - цель, А - средство.
3. Отсюда
строим установку: любая теорема может быть доказана из закона
тождества.
4. Посмотрим, как формируются правила вывода на основании
таблиц.
4.1. Определение оператора. Что делает оператор.
Оператором выделяются истинностные значения "истина" и "ложь" для наборов
истинностных значений переменных. Так, для дизъюнкции исключается 4-я строка
наборов
как ложная.
Если мы рассматриваем правила удаления, то первое, что мы делаем, мы смотрим,
какие строки из набора истинностных значений переменных
оператором
выделяются в качестве истинных. Возьмём конъюнкцию А&B. Конъюнкция
истинна только для первой строки наборов, в которой обе переменные принимают
значение "истина". Поэтому непосредственно из оператора конъюнкции выводимо А и
выводимо В. Если мы возьмём отрицание импликации, то в ней истинной будет вторая
строка, то есть истинными будут А и -В, и поэтому они непосредственно выводятся.
И т.д.
4.2. Если же выделяются три строки со значением "истина",
то, естественно, ситуация изменяется. Оператор дизъюнкции истинен для первых
трех строк. С целью дальнейшего ограничения рассматриваемых истинных строк
фиксируем переменную А. Если А истинно, то В может быть истинным или ложным,
следовательно, однозначного вывода сделать нельзя. Если А ложно, то это
соответствует 3 и 4 строкам. 4 строка не принимается во внимание, а в 3 строке В
истинно. И, точно также, если мы примем В, то ему будут соответствовать А как
истинное, так и ложное, поэтому однозначный вывод невозможен. -В соответствуют
строки 2 и 4. Так как четвертая строка не рассматривается, то остается только
вторая строка, для которой А истинно.
4.3. Т.о., при посылке -А выделяется 3 строка, при
посылке -В выделяется вторая строка. То есть выделяются разные строки. Но как же
так получается, что эти два разные по сути дела правила вывода дают одинаковые
истинностные таблицы для оператора дизъюнкции? Создается впечатление, что при
этом в обоих случаях к выделенной строке, связанной с выводом, добавляются еще
две строки, которые явно не выделяются, но которые соответствуют дизъюнкции.
Выбор -А оставляет не выделенными две строки с А. И, аналогично, для -В остаются
не выделенными строки 1 и 3. Т.о., мы имеем, соответственно, строки, которые, с
одной стороны, занимают и А и -А, с другой - и В, и -В. Они берутся в качестве
посылок. Так как А не дает однозначного вывода, то оно явно и не
рассматривается. И то же относительно В.
4.4. Для сравнения обратимся к эквивалентности. В ней не
рассматриваются, и в этом смысле удаляются 2 и 3 строки. И выводы получаются из
А, из -А, из В, из -В. В связи с этим, можем допустить, что если и А, и В
выделяют общие им обоим строки, то независимо от строки, из которой получается
однозначный вывод, в целом мы получаем одинаковые истинностные таблицы
операторов.
5. Но тогда мы можем говорить о формировании самих
операторов. Например, каким образом формируется дизъюнкция? Дизъюнкция
формируется таким образом, что в ней переменным А и В соответствуют
противоположные истинностные значения, а переменным -А и -В ставится в
соответствие истинностное значение "истина" В и А . Теперь на
основании этого принципа мы можем создавать определения для других (возможных)
операторов. Например, мы можем допустить, что выбор и -А, -В
порождает противоположные значения другой переменной "и", "л", то есть -А
соответствуют В и -В, а -В соответствуют А и -А. А А, соответственно, даёт -В и
В даёт -А. Что в результате этого мы получим? Так как -А, -В соответствуют два
противоположные значения В, А, то это соответствует трём последним строкам
таблицы истинности, при которых оператор принимает значение "и". Так как, далее,
А соответствует -В (вторая строка таблицы истинности), В соответствует -А
(третья строка таблицы истинности), то мы получили таблицу истинности для
антиконъюнкции. Мы замечаем, что технология при создании операторов состоит в
том, что вначале мы придаем двум переменным некоторое значение и рассматриваем
строки, в которых другая (противоположная) переменная принимает значения "и",
"л". В результате этого мы получаем какие-то три строки и полагаем, что в них
оператор принимает истинностное значение "и". Четвертая строка рассматривается в
качестве ложной. Затем каждой из переменных мы придаем противоположное
истинностное значение и смотрим, какое истинностное значение при этом принимает
вторая переменная и т.о. получаем правила удаления оператора. Еще пример. Пусть
-А влечет В и -В, В влечет А и -А. Выделенными окажутся 1,3,4 строки. Придаем
каждой из переменных противоположные ранее принятым значения. Тогда А будет
соответствовать В, -В будет соответствовать -А. Нами получен оператор импликации
и правила вывода для него. Пусть теперь А влечет В и -В, -В влечет А и А.
Это 1,2, 4 строки. Придаем переменным противоположные значения. Тогда -А будет
влечь -В, В будет влечь А. Это - обратная импликация с её правилами удаления.
6. Допустим, что А влечет В, -А влечет В. То есть из А&-A следует В. Это
означает, что В не зависит от А. А&-А всегда ложное , но с т.зр.
объективиста - истинное высказывание, которое утверждает, что, с
одной стороны, нечто есть А, с другой стороны, нечто есть -А, причем, и
одно, и другое высказывания одинаково истинны. Это означает, что различие
отношений, в которых рассматриваются высказывания, выносится за скобки, и эти
два высказывания отождествляются. И тогда объективистом высказывания
рассматриваются как одинаково истинные. Это ставит субъекта по отношению к
реальности в теоретическую позицию, которой исключается всякое практическое
участие его в ней. Это - пример высказывания, когда отсутствует
фиксация субъекта ни на одной стороне противоположности.
1. В процессе мышления нужно задаваться вопросом, что
чему противостоит. Применяется противопоставление чего-то чему-то.
2. Закон тождества или закон отражения. Отражаться может
всё, что угодно,
в том числе и связи,
и отсюда - правило подстановки в закон тождества. Поэтому
из А~A следует A→B~A→B. Затем, если есть подстановка, выражающая связи, то
возможно множество её форм: А→В, -А→В, А→-В, -А→-В, и , соответственно,
операторы, представляющие собой отрицание существования связей в форме отрицания
импликации: -.А→В, -.-А→В, -.А→-В, -.-А→-В, всего, т.о. 8 операторов, постоянно
применяемых на практике.
3. Прямой импликации соответствует обратная импликация. В
свою очередь, обратной импликации А←В соответствует прямая импликация В→А.
Сказать А←В и сказать В→А - это разными способами сказать одно и то же, но при
этом рассматривая высказывание с разных точек зрения. Различие состоит в смене
местами субъекта и предиката суждения (антецедента и консеквента высказывания),
то есть того, о чем мы говорим и того, что мы говорим. Если мы говорим А←В, то
мы говорим об А, и утверждаем относительно него, что имеет место А, если имеет
место В. Если же мы говорим В→А, то мы высказываемся о В, и утверждаем, что
следствием из него является А. А это означает также, что когда мы говорим об
операторах, например, о симметричных и несимметричных, то два противоположных
отношения, с которыми мы имеем дело, связаны с тем, что мы должны, обязаны, в
силу эквивалентности закона тождества, брать при рассмотрении прямую и обратную
импликации. То же, что мы делали, это, переставляя антецедент и консеквент
импликации явным образом, неявно применяли оператор обратной импликации.
4 Противоположности. Если А→В~ -B→-A, то А→А ~ -A→-A. Эти вещи выражают отношения между противоположностями. Также выражают отношения объективации и субъективации. Что такое субъективация - это включенность в процесс. Объективация - это отключенность от него. Что такое А→В→.А→В. Тут отношение включенности. Что представляет собой выражение А→В→. -В→ -А. Это наблюдение процессов в противоположности с точки зрения критериев наблюдателя, которые рассматривают в форме отрицания истинность другой стороны противоположности, положения которой определяются в качестве возмущающих факторов. Факты противоположной для данной стороны противоположности выступают в ней в отрицательной формы относительно её собственных положений. То есть здесь единственное, что она может сказать, что здесь речь идёт о -В и -А, то есть об отрицании В и А, но каково истинное содержание этого -В и -А, она сказать не может. Она может говорить только о том, каким образом, в какой форме отражается это содержание в ней. Ибо судить о содержании противоположности она может только через рассмотрение собственных содержаний как истинных, как тех критериев, посредством которых она только и способна оценивать содержания противоположной стороны. В этом заключается смысл формального отрицания, не схватывающего содержания противоположной стороны. Т.о., с какого рода процессами, отношениями мы имеем дело. Прежде всего, с противоположными. Именно, если в одной стороне противоположности процесс идет от А к В, то для противоположной стороны противоположности характерно противоположное направление процесса, от -В к -А, и, сл., взаимоотношение между противоположностями, рассматриваемое в качестве процесса, характеризуется тем, что если возникновение, становление А порождает возникновение, становление В, то -В есть отрицание становления В, и в этом смысле подавление В посредством становления и развития -А, направленного на подавление А. Если мы поменяем точку зрения на противоположную, то там нам откроется точно такая же картина. Т.о., мы имеем дело с двумя противоположно направленными силами, которые так или иначе уравновешивают друг друга. И мы, т.о., имеем дело с той или иной формой единства противоположностей, при которой каждая из сторон противоположности не только отрицает другую, но и предполагает её существование и тем самым не уничтожает до конца. И поэтому мы будем иметь дело с колебаниями между сторонами противоположностей, но не с их взаимным уничтожением. Тем не менее, мы должны задаться вопросом относительно того, что происходит, когда одна из сторон противоположности целиком вытесняет другую. Но отсюда, мы получаем, во всяком случае, количественные характеристики для А и В. Именно, если, например, А равно 3/4, В=1/4 , то, соответственно, -В будет равно 3/4, -А=1/4. Но если величины 1/4 и 3/4 обозначают расстояния относительно полюсов противоположностей, то есть относительно их значений 0, 1, то сам процесс определяется соотношением сил противоположных сторон, что отражается в скорости и ускорении движения процессов в том или ином направлении относительно сторон противоположностей. А также функциональной зависимости сил от расстояния от полюсов сил, характеризующих А и В, а также функциональную зависимость между А и В.
Какую функцию выполняют законы логики тождества, исключенного третьего, непротиворечия. Все они служат одной цели: фиксации на одной стороне противоположности, введение, т.о., односторонности, исключение из рассмотрения другой стороны противоположности. Если мы говорим об А, то не имеем права говорить в то же самое время о -А, и именно потому, что -А представляет противоположное содержание, а противоположные содержания хотя в основе своей и предполагают друг друга, но всюду, где речь идет о практических отношениях, они друг друга исключают. Можно сказать, что законами логики обеспечивается единство в процессе преследования человеком или группами людей их интересов, так как признание наряду с их собственными интересами также и противостоящих им интересов обезоруживает их.
07.05.12 г