Заметки по философии логики.

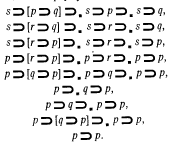
Хороший пример применения переименования
переменных в доказательствах дан Черчем в его "Введении в математическую логику"
ИЛ, М,1960 стр.75 (рис. вверху справа). Для доказательства р→р
им берется аксиома 103, в которую на место р подставляется r:
p/r, получаем s→(r→q)→.s→r→.s→q,
затем делается подстановка q/p, получаем
s→(r→p)→.s→r→.s→p,
затем подстановка s/p, получаем p→(r→p)→.p→r→.p→p
, наконец, r/p: p→(q→p)→.p→q→.p→p
, откуда применением аксиомы 102 получаем выводимость
p→q→.p→p,
подставляем q/q→p получаем р→р.
Если вы захотите в этом увидеть какую-то логику, вы вряд ли её найдете. Всё, что
происходит, похоже на игру: заданы какие-то правила, и вы действуете в
соответствии с правилами, и этого оказывается достаточно. В чем черчевская
особенность. Формально p,q,r,s переменные,
принимающие одно из двух возможных и исключающих друг друга значения -
t, f - "истина" и
"ложь". Однако особенность здесь в том, что у него в действительности переменные
высказываний - на деле это какие-то конкретные высказывания. А каждое конкретное
высказывание является истинным или ложным. То есть любое конкретное высказывание
на деле уже является переменной, которая является истинной или ложной. С самим
по себе высказыванием его истинностное значение непосредственно не связно,
истинность высказывания определяется обстоятельствами, которые лежат вне его, и
его истинность характеризуется двумя обстоятельствами, способными содержательно
переходить друг в друга: тем, чем объективно является высказывание и тем, как
субъективно к нему относятся - как к истинному или ложному. Всё это означает,
что Черч в качестве истинного позитивиста не знает общих понятий, не знает идей,
которыми представляется понятие как общее, обозначающее объекты. И поэтому
он оперирует только конкретными объектами. И, в частности, конкретными
суждениями. Разумеется, любое конкретное суждение может сокращенно обозначаться
буквами. Но следует иметь ввиду, что за этой буквой стоит некоторое
содержательно определенное, осмысленное или бессмысленное суждение, которое и
является истинным или ложным. Мы вообще приходим к понятию формы мысли и,
соответственно, к понятию логики, когда рассматриваем высказывания,
абстрагируясь от их истинностных значений. Что такое форма мысли? - это
всегда истинное высказывание, то есть высказывание, истинностное значение
которого не зависит от истинностных значений входящих в него переменных. При
этом высказывание всегда истинное рассматривается как тождественное,
высказывание всегда ложное - как противоречие. Но так как отношение между
тождественными высказываниями и противоречивыми представляет собой их взаимное
отрицание, то и получается, что из двух противоположных высказываний неважно,
какое из них назвать тождественным и какое противоречивым. Определив одно из них
в качестве тождественного, мы тем самым противоположное определяем как
противоречивое, как и обратно, определив одно в качестве противоречия, его
отрицание мы тем самым должны будем определить как тождественно - истинное.
С другой стороны, если всегда истинное высказывание есть тождественно-истинное,
то тогда отрицающее его высказывание будет тождественно ложным, и тогда с
противной стороны. Тогда чем хуже этих наименование наименование противоречиво
истинное и противоречиво ложное высказывание для всегда ложных и всегда истинных
высказываний соответственно?. Действительно, чем лучше одна другой формулы
Av-A = и и А&-A=л.
Нам достаточно одну из этих формул взять с отрицанием для того, чтобы были
получены две в содержательном отношении тождественные формулы, различающиеся
друг от друга только по форме. Особенность человеческого мышления состоит
в том, что оно из двух противоположных сторон фиксируется на одной из них, и при
этом связь с противоположной стороной осуществляется через её отрицание. А тогда
получаем и два возможных способа мышления: одно мышление исключает из
рассмотрения всякое противоречие, и тогда оно будет оперировать двумя формулами
Av-А и -(А&-A),
и второй способ мышления, который, напротив, исключает из рассмотрения всякое
тождество: A&-A, -(Av-A). Пожалуй,
подобного рода мысль может вывести из себя правоверного логика. Но он на то и
правоверный, чтобы возмущаться. Мы же поставим вопрос иначе: в живых системах
побеждает целесообразность. То, какой из двух способов мышления выходит на
передний план в мышлении, определяется эффективностью решаемых задач тем либо
другим способом мышления в предлагаемых обстоятельствах. Библия гласит: не
возлюби жены ближнего своего - мышление посредством закона тождества. Но иметь
жену и одновременно любовницу - это сладко, а что доставляет удовольствие, то и
истинно - это мышление посредством закона противоречия. И на деле мы тогда,
когда нам это предоставляет выгоду, пользуемся одним законом, и когда доставляет
удовольствие - другим. Следование в жизни двум противоположным законам мышления
- в нашей крови. Наша кровь заражена богом и дьяволом, чистотой и грязью. Кому
то это может нравиться, кому-то - нет. Но это - есть.
Спрашивается, для чего Черчу понадобилось делать последовательно 4 подстановки p/s, q/p, s/p, r/q, когда задачу можно решить одной подстановкой s/q и мы получили бы
q→(p→q)→.q→p→.q→q.
Да потому, что для позитивиста высказывания s→(p→q)→.s→p→.s→q
(1) и s→(r→q)→.s→r→.s→q
(2) - это различные конкретные объекты, а отождествляться
между собой могут только одинаковые объекты. И оперировать возможно только с
конкретными объектами. Конкретика, оперирование конкретными объектами - ключевой
принцип позитивизма. Для позитивиста объекты (1), (2) - это разные
объекты. Для идеалиста объекты (1), (2) - это одинаковые объекты, и
именно потому, что объекты (1), (2) он рассматривает как явление сущности, в
качестве каковой для него выступает общая обоим объектам форма,
определяемая структурой, , то есть одинаковыми отношениями элементов в объекте.
Пусть какое-то положение истинно т.о., что оно истинно независимо от того,
является истинным или ложным какое-то другое положение контекста, в который оно
входит. Если положение А истинно само по себе (является причиной самого себя),
что может быть выражено как А->A, или А=А, то мы можем записать: (А=А) →(Вv-B→.А=А),
то есть объект А является истинным независимо от того, является В истинным или
ложным.
Эту формулу можно назвать аксиомой независимости. Когда мы рассматриваем
какое бы то ни было положение, мы можем не знать, является оно зависимым или
независимым от других положений. Как мы можем установить его зависимость или
независимость от других положений? Мы должны взять их с отрицанием. Если их
отрицание никак не отражается на нашем положении, то сможем сказать, что оно не
зависит от них, если же его истинностное значение изменится, то должны будем
записать, что данное положение является следствием.
В связи с этим мы можем сделать принципиальное разделение, именно, независимые
положения от других положений, но зависящие только от самих себя, мы должны
будем записать в виде тождества А=А, откуда А→А,
зависящие - в виде В→А.
Теперь проследим доказательство Черча в обратном порядке. Берем независимый объект А
А. На основании аксиомы независимости можем записать: В→.А→А. Для того,
чтобы рассматривать объект А в качестве следствия из объекта В, объект В также
должен быть независимым объектом, то есть иметь вид В→В.
С другой стороны, каким образом, на основе чего мы можем придти вообще к понятию
связи. Для этого нужно иметь дело в прямой и обратной операциями, что означает,
что если мы можем от А перейти к В, то обратной будет операция перехода от В к
А, что на языке логики называется эквивалентностью. Со связями мы имеем
дело с таким положением вещей, что либо связь является односторонней, либо
двусторонней. Если связь односторонняя, то она не имеет обратной операции, и мы
не можем возвратиться в исходный пункт движения. Поэтому