| Пусть в пространстве летит стрела. Если
стрела летит, то её положение рассматривается по отношению к точкам
пространства. Сама по себе стрела как целое представляет собой
некоторую единицу, которая занимает в пространстве некоторое место,
представляющее собой множество упорядоченных точек, где под
точкой понимается универсальное понятие, такое, что точка
может принимать любую величину относительно любого из возможных
направлений, и эта величина зависит от направления и скорости
движения стрелы и величины времени, которыми измеряются как
аргументом функции пространственные значения величины точки
как единицы измерения (Это определение точки по сути своей
представляет частное, которое рассматривается сквозь призму
всеобщего, включающего в себя, наряду с частностью точки,
также и остальные пространственно временные частные категории
пространства - линии, плоскости и т.п., при определенных условиях
переходящие друг в друга. Можно не зацикливаться на этом
определении, если нет нужды в нём) Итак, стрела летит. Допустим, что полет её прямолинеен. Рассматриваем проекцию полета стрелы на прямую линию плоскости пространства, параллельную полету стрелы. Замечание. Противоречие, которое объективно вводится, состоит в том, что время отождествляется с двумя противоположными понятиями: понятием момента времени, что означает по сути своей определение времени как фиксированной величины, в то время как время принципиально есть величина переменная и в любом случае представляет собой некоторый интервал, то есть представляет собой процесс, а не результат, не ставший объект. Между тем, какие-то его отрезки рассматриваются как единицы, то есть как то, что представляет собой ставшую величину. С физической, вообще с практической стороны отношений субъекта с объектом необходимость введения такого противоречия заключается в характере отражения сенсорными системами внешней среды, связанном со степенью их чувствительности, за пределами которой изменяющаяся величина рассматривается (выглядит, воспринимается) в качестве постоянной. Отсюда возникает и понятие единиц измерения. Например, час как процесс может измеряться минутами, или секундами, или чем-то меньшим. Но на деле и минуты, и секунды, при том, что они рассматриваются как постоянные, неизменные величины, в себе есть какой-то определенный, фиксированный интервал изменений. В свою очередь, год может измеряться часами, и т.п. Единицам противостоит то, что они измеряют. Это - две необходимые противоположные стороны, определяющие друг друга. Одна постоянная величина, единицы, то, при посредстве чего осуществляется измерение, противопоставляется другой постоянной величине - то, что измеряется. Изменения, которые происходят в интервале времени единицы, не учитываются. Учитываются только изменения, накопленные за единицу измерения. И эти накопленные за единицы времени изменения суммируются. Таким образом, за постоянными величинами как того, что измеряется, так и того, при помощи чего осуществляются измерения, скрываются своеобразные контейнеры, накопители изменений за какие-то постоянные интервалы времени. И, т.о., непрерывное выражается не непосредственно, а опосредованно, через дискретное. 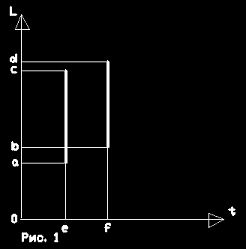 Эта проекция представляет собой некоторый интервал точек (а,...,в) в момент времени t=е. Возьмём сколь угодно малый отрезок времени ∆t=f-e. За этот отрезок времени стрела изменит своё положение в пространстве с положения (а, с) на положение (b,d). Это изменение может быть выражено в виде S(f-e)=(b,d) - (a,c)= ((b-a),(d-c)) Процесс изменения проекции стрелы в пространстве состоит в том, что за время f-e, с одной стороны, возникает приращение проекции на величину d-c и, с другой, противоположной стороны, уменьшение её проекции на ту же величину b-a. В результате этого сама по себе проекция стрелы в пространстве остается постоянной независимо от того, какие интервалы времени полета стрелы мы ни брали бы. Величина проекции стрелы пространства постоянна, но изменяются места положения стрелы в пространстве, и именно на основе того, что приращению проекции точек стрелы в пространстве соответствует уменьшение их на точно такую же величину. Т.о., летящая стрела в пространстве занимает равное себе место, и в этом смысле она постоянна. Но в полете стрела изменяет своё место в пространстве. И это изменение стрелой своего места в пространстве называется её движением в нём. |
|||
| Парадокс Зенона. "Летящая стрела неподвижна, так как в каждый момент времени она занимает равное себе положение, то есть покоится; поскольку она покоится в каждый момент времени, то она покоится во все моменты времени, то есть не существует момента времени, в котором стрела совершает движение."(формулировка из Википедии) У Зенона не летящая стрела берется по отношению к пространству, а пространство берется по отношению к стреле. Пространство, взятое по отношению к стреле, есть постоянный отрезок точек, принадлежащих стреле. Так как этот отрезок точек в течение всего полета стрелы остаётся постоянным, то стрела остается тождественной самой себе и, т.к. в ней не происходит никаких изменений, то она покоится. Если мы перевернем это отношение и будем рассматривать не свойства пространства относительно стрелы, а свойства стрелы относительно пространства, то обнаружим, что при всём том, что стрела остается самотождественной самой себе, она изменяет своё место в пространстве. Следовательно, относительно пространства она обладает свойством изменения, и именно, свойством движения. Движенья нет, сказал мудрец брадатый. Другой смолчал и стал пред ним ходить. Сильнее бы не мог он возразить; Хвалили все ответ замысловатый. Но, господа, забавный случай сей Другой пример на память мне приводит: Ведь каждый день пред нами солнце ходит, Однако ж прав упрямый Галилей. А.С. Пушкин. "Движение" В то же самое время, о чем говорит нам наш инстинкт? О том, что во время движения длина стрелы должна изменяться: начало стрелы встречает сопротивление, и оно должно укорачивать стрелу в начальной её части. Если стрела встречает сопротивление, которое стремится замедлить её движение, то все последующие точки от начала должны "наваливаться" на начальные вследствие существующего торможения, и стрела в целом должна укорачиваться. Особенно это должно проявляться в условиях изменяющегося сопротивления среды: чем больше сопротивление, тем сильнее должна укорачиваться стрела, и, напротив, при уменьшении сопротивления стрела должна удлиняться. Если скорость полета стрелы постоянна, то ей должна соответствовать и постоянная длина стрелы. Изменение постоянной скорости на постоянную же другой величины должно влечь за собой изменение её длины. Относительные изменения длины стрелы в разных средах сопротивления для различных скоростей полета стрелы незначительны и не учитываются. Впрочем, это уже другая тема. 09.07.11 г |