При этом здесь следует поступить так, как это делают математики, а именно, исходить не из того, что мы имеем дело с чем-то нераздельным целым, а из того, что существует множество независимых совместно действующих объектов. При этом здесь получается такая картина, что есть множество воздействующих отдельностей, каждая из которых действует по-своему и даёт свой результат, а уже их совместное действие дает общий результат. Другой , дополняющей стороной этого же подхода является математическое понятие функции. Пусть х=2t. Эта функция есть какой-то преобразователь. Изменение t дает изменение значения х. Но в общем и целом за параметром 2 скрывается, в свою очередь, какая-то функция от t. А это означает, что за целостным результатом следует видеть не только совместное действие независимых многих, но в том числе и их функциональную связанность.
Однако на а достаточно коротком интервале времени функциональные зависимости частей целого (то есть отдельностей) могут быть вынесены за скобки (не учитываться).
Но для того, чтобы иметь дело с отдельностями, отдельности должны быть раньше образованы. Методология заключается в том, что для обеспечения вычислений значения целого мы должны раньше выделить в нём отдельности, и уже на основании осуществленного расчленения целостности осуществлять вычисления, которые будут характеризовать целостность.
Итак, подход заключается в том, что на основании знания совместного действия каждой из отдельностей целого определяются результаты их совместного действия как действия целостности.. Это означает применение аксиомы: действие каждой из отдельностей независимо от действия всех других отдельностей. Предполагается, что ни одна из отдельностей не оказывает влияния ни на какие другие отдельности.
Связь с. Каждая связь является единственной и состоит из двух точек и одной линии, связывающей точки:с=с(2т,1л), где Т- множество точек, т-точка, Л- множество линий, л- линия, {c} - множество связей, с- связь, и т, л, с - переменные, определенные на соответствующем им множестве.
Каждая точка т может принадлежать множеству связей {c}.
Множество связей {c} образуют сеть С.
Связи могут быть актуальными и потенциальными. Связи могут характеризоваться временем жизни; они могут образовываться и разрушаться. Соответственно, сеть может быть потенциальной и актуальной. Актуальная сеть образована множеством связанных точек. Потенциальная сеть образована множеством связанных точек и точек, которые потенциально могут стать связанными.
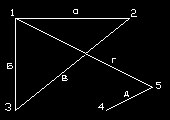
То, что всякая связь с образована 2т и 1л, позволяет представить сеть в матричной форме.
| т\л | а | б | в | г | д |
| 1 | + | + | + | ||
| 2 | + | + | |||
| 3 | + | + | |||
| 4 | + | ||||
| 5 | + | + |
 Одна линия, связывающая
две точки, может интерпретироваться и как обозначающая некоторое одно
отношение, и как множество отношений. Отношение может быть
однонаправленным или двунаправленным. Направленные линии будем
называть векторами, а соответствующие им связи -векторными. (напр.,
отношение "хозяин-работник" представляет собой двунаправленный вектор)
Одна линия, связывающая
две точки, может интерпретироваться и как обозначающая некоторое одно
отношение, и как множество отношений. Отношение может быть
однонаправленным или двунаправленным. Направленные линии будем
называть векторами, а соответствующие им связи -векторными. (напр.,
отношение "хозяин-работник" представляет собой двунаправленный вектор) Две точки могут соединяться множеством линий, которые могут интерпретироваться как множество отношений, связывающих точки.
Сами точки представляют объекты
Линия может начинаться и оканчиваться на одной точке (пример: натуральное хозяйство)
Сети определяются по типу допускаемых в них связей.
С - сеть, в которой употребляемые типы связей не оговариваются.
Эти связи могут быть следующих типов:
1. с=с(2т,1л)
2. с=с(2т, nл), где пл - потенциальные линии
3. с=с(1т,1л)
4. с=с(2т,вл), где вл- линия-вектор
5. с=с(2т, мл) , где мл - по крайней мере две линии, связывающие точки
Если с=с(2т, вл)=вл(т, т), то вл(т,т) обозначает вектор, начинающийся в левой точке и заканчивающийся в правой, то есть вл(т1,т2) и вл(т2,т1) описывают противоположные векторы.
Соответственно, получаем С1 - сеть, в которой допускаются связи 1-го типа.
С13 -сети, допускающие связи 1, 3 типов. И далее понятно:
С12 , С123 , С4 и т.п.
Но возможен и другой способ классификации, основывающийся на операции ограничения. Если примем сеть типа С в качестве сети, которой допускаются любые типы связей, то ограничение может начинаться с того, что допускаются только актуальные связи, то есть связи, которые не рассматриваются в их изменении во времени. С-2 , не потенциальные и не векторные С-2,4 , и не допускаются петли С-2,3.4 , и не допускаются мультилинии С -2,3,4 ,5 и т.п.
Другие названия:
точки - узлы, вершины
линии - ребра,
Точкам и (или) линиям могут приписываться веса для моделирования времени, расстояния, стоимости, вероятности и т.п.
Например, точка тa - покупатель, точка тb - продавец. Точка т может представлять объект, который обладает множеством признаков, например, можно говорить о весе т в смысле количества денег д, с одной стороны, и потребности в товаре т - с другой. Если в числителе изображать позитив, или средство ср, или то, что может быть отчуждено, а в знаменателе - негатив, или цель ц, или то, что должно быть приобретено, то этот вес может быть представлен в виде д/т, например, 50р/1т. В свою очередь, продавец имеет товар в качестве средства и деньги в качестве цели, то есть т/д, например, 1т/60 руб. Для того, чтобы между покупателем и продавцом мог совершиться обмен, необходимо, чтобы позитивы и негативы покупателя и продавца во всяком случае совпали. ср1/ц1=ср2/ц2, откуда ср1*ц2=ср2*ц1. В каждой из дробей выражаются идеальные отношения стоимости: у покупателя - стоимость товара в денежном выражении, у продавца - стоимость денег в товарном выражении. И это - идеальная сторона. Средство одного должно совпасть с целью другого, реальность одного с идеальностью другого. Между покупателем и продавцом устанавливаются отношения “торговли”, это - две линии-вектора от одного к другому, которые вначале торговли разнятся между собой. Когда между идеальными и реальными величинами каждого из них устанавливается равенство, совершается обмен, и мы получаем удовлетворенные потребности с одной и другой стороны, в результате чего связь распадается. Точка со стороны своих положительных и отрицательных признаков может изображаться в виде т(а/b,c/d,...,) Потребность и средства для её реализации оказываются теми силами притяжения, на основе которых устанавливаются отношения между живыми системами вообще, и людьми в особенности. Мы имеем здесь пример установления связи одного элемента с другим, одной точки с другой. Т.о., если мы имеем две точки, то вопрос об установлении связи между ними связан с интересами каждой из точек относительно другой, и именно, если та (а/b)& тb (b/a), то в случае их равенства в результате обмена получим тa(b)& тb(a), т.е. f(тa (а/b) & тb (b/a))=тa (b)&тb (a)
Примечание относительно знаков равенства = и стрелки → . Будем считать, что знак равенства обозначает актуальное действие, не предполагающее процесса между левой и правой частями формы А=В, тогда как применение стрелки в форме А→В обозначает процесс, переход, последовательность состояний, преобразования А в В.
Тогда обмен вместе с предваряющим его с процессом уравнивания позиций покупателя и продавца может быть представлен в виде f(тa (а/b) & тb (b/a))→тa (b)&тb (a), а если считать, что исходным пунктом движения для покупателя и продавца были их цели , ради которых они создавали свои средства, то последнему выражению должен предшествовать процесс создания средств реализации цели: тa(ц/ср)→тa(ср/ц), и то же относительно тb.
Метазамечание 1. Связка “если...., то” может преобразовываться в функцию, как и обратно.)
Метазамечание 2. Нужен перевод читаемого на свой язык, так как только в этом случае ты будешь понимать то, о чем читаешь. Такой перевод означает не что иное, как перевод чужой карты мира в свою карту мира.
Будем рассматривать сети типа С1
Множество связей, в которые входит точка (которыми обладает точка), называются степенью точки . Если точка - объект, и множество её связей - её признаки, и признаки будем обозначать в качестве верхнего индекса объекта т, и объект - общее понятие объекта, и поэтому объект т есть переменная, принимающая значения из множества объектов, и т с нижним индексом обозначает элемент из этого множества (единичный объект) и признак числа степеней точки обозначим d, то можем записать тid =k. Если тid =1, то тi - тупиковая точка, если тid =0, то тi - изолированная точка. За этой записью скрывается важная вещь, связанная вообще со способом образования сетей.
Если дано множество {c(т,л)}, то на его основе может быть построено множество сетей {C} посредством совмещения точек тi связей с и редуцированием совмещенных точек в одну точку. Поэтому запись вида тid =k обозначает множество совмещенных точек в одной редуцированной точке. И так как л=2т, то множество тid представляет множество точек связей, совмещенных в одной точке, а это означает представление сети без операции редуцирования точек, то есть каждая из точек связей в сети сохраняется. Эту "недоделанную" сеть обозначим как сеть С минус операция редукции -р : С-р . Так как сеть С-р представляет о.о. упорядоченное множество связей, в которых по крайней мере некоторые точки одних связей устанавливаются в 1-1-значное соответствие с одной из точек других связей, то все связи остались неизменными, и поэтому соотношение между числом точек и связей сохранятся такое же, как и для отдельной связи, то есть 1/2: т=2л.
Вводя понятие степени точки, мы тем самым переходим к общему числу точек сети С. Выражение тid =k может быть преобразовано в выражение d(тi )=k, или сокращенно di и отсюда, если мы возьмём сумму степеней всех точек, то получим ∑i=1T di =2Л. (1)
Следствие из (1). Число точек нечетной степени в сети С1 четно, так как в ней сумма степеней точек является четной, а следствием допущения нечетности числа нечетных вершин в сумме оказалось бы нечетное число степеней.
связи на основании признаков точки
точек как целое