| |
Во всем употребляемом нами множестве чисел уже предполагается
единица, которая выступает в качестве единицы измерения, то есть в
качестве того общего, единого, которое употребляется одинаково для всех.
Это означает, что всюду мы имеем дело с одним и тем же объектом. То есть
с одной и той же физически данной величиной. Например, мы говорим «5
бидонов молока». Что это означает? Что бидон – это единица измерения,
которая измеряется количествами, скажем, литров молока, например, бидон
содержит 18 литров молока. Мы, т.о., имеем дело с противоположностью.
Во- первых, с единицей объектов одного рода и с единицами объектов
другого рода. Мы также имеем дело с отношением принадлежности, где под
этим термином понимается отношение принадлежности в широком смысле. Мы
умножаем количество бидонов на количество литров молока, умещающегося в
бидоне, и мы получаем в результате этого количество молока. У нас была
отдельно взятая единица измерения, эта единица измерения была
подразделена на множество более мелких единиц, соизмеримых с исходной, и
тогда множество единиц измерения, умноженное на определенное в ней (по
отношению к ней) множество субъединиц дало нам более мелкие единицы
измерения. То есть 5 бидонов мы умножаем на 18 литров молока, и получаем
90 литров молока. |
|
| |
Под практической соизмеримостью единиц понимается
случай, когда единицы укладываются в некоторой единице целое число раз.
Соизмеримые единицы получаются посредством операции деления, которая
может рассматриваться в качестве производящей соизмеримые единицы. Если
единица а=15 см, единица б=7 см, то эти единицы в данном их виде не
соизмеримы, так как 7 в 15 не укладывается целое число раз. Мы можем,
конечно, перейти к единице с=1, которая будет соизмерима и с 15, и с 7,
но если у нас ящик длиной в 15 см, а изделие имеет длину 7 см., то для
нас уже не имеет значения, что для 15 и 7 можно найти соизмеримую
единицу. Нам нужен ящик, кратный 7, если брать, соответственно,
внутренние размеры ящика и внешние размеры изделия и не учитывать
необходимые припуски на вложение изделий в ящик. Это соотношение мы
можем пропорционально уменьшать или увеличивать сколько угодно раз, от
этого несоизмеримость этих двух единиц никуда не денется. Чтобы
получить соизмеримую с 15 и 7 единицу, их перемножить. Но это уже
будет третья единица измерения, которая ничего не меняет в отношениях
между 15 и 7. И подобного рода несоизмеримых единиц вы найдете сколько
угодно. Все числа натурального ряда соизмеримы с единицей, но единицы 2
и 3, 3 и 4 несоизмеримы друг с другом, тогда как 2 и 4 - соизмеримы.
Т.о., когда речь идет о соизмеримости двух единиц, то можно говорить о
соизмеримости лишь в том случае, когда одна из единиц в точности целое
число раз умещается в другой. В противном случае они не соизмеримы.
Отрезок, равный 6, соизмерим с 2 и 3, но это обстоятельство не делает 2
и 3 соизмеримыми друг с другом.
В практической
деятельности положение вещей таково, что нами одни единицы соизмеряются
друг с другом, и мы целенаправленно производим соизмеримые единицы.
|
|
| |
С другой стороны, деля 90 литров молока на 5 бидонов, мы получаем
количество элементов, которые находятся в бидоне как единице измерения,
либо же деля количество молока на число единиц, принадлежащее ёмкости
бидона, мы получаем количество бидонов. Т.о., бидон как единица
измерения выступает как контейнер, который вмещает в себя какие-то
элементы. В этом случае мы можем говорить о бидоне и его ёмкости, и,
соответственно этому, о единице и её ёмкости. В этом смысле что такое
отдельно взятый бидон?- это элемент множества бидонов. Что такое его
ёмкость? это элементы такого множества, как бидон. |
|
| |
По отношению к бидону могут быть взяты другие более крупные
единицы, например, кузов машины, в который вмещается какое – то число
бидонов, и, соответственно, множество машин и т.п. В результате получаем
дерево с вершиной уровня nmax
, такое, в котором каждый узел уровня n, за исключением уровня n≠1, то
есть уровня «листьев дерева», выступает в качестве единицы, в отношении
к которой уровень n-1 множества узлов дерева, связанных ветвями с ней,
выступает в качестве элементов этой единицы, представляющей, т.о.,
соответствующее множество как единство отношения предиката и его
денотата (объёма соответствующего предикату понятия). И т.о. мы получаем
общую закономерность, которая связывает все узлы
(узловые элементы) дерева.
Этому соответствует и способ подсчета. Если мы имеем вершину nmax
дерева, то она выступает в качестве самой крупной единицы измерения.
Тогда мы получаем произведение вершины nmax
дерева (=1)на число её узлов (элементов) уровня (n-1). Если мы
имеем дело с узлом уровня n дерева, который не
является ни его вершиной nmax
, ни его листом, то мы получаем, например, 3 машины (три узла и,
соответственно, три единицы), в каждой машине (в каждом узле как
определенной единицы) 5 бидонов (число субъединиц, содержащихся в
единице), и в каждом бидоне 18 литров молока. Тогда мы 3 умножаем на
пять, получаем 15 бидонов, и затем 15 бидонов умножаем на 18, и получаем
270 литров молока. То есть каждому элементу множества машин как единице
измерения ставится в соответствие по 5 субъединиц множества бидонов, и
т.д. |
|
| |
На какую особенность необходимо обратить внимание? Мы три
машины умножаем на 5 бидонов, и получаем 15 бидонов. Но ведь мы умножали
машины на бидоны, и, значит, должны были получить 15 машино-бидонов, а
вместо этого говорим о бидонах. С другой стороны, разделим 15 бидонов на
пять, получим три машины. То есть из бидонов явились на свет машины.
Значит, машины куда-то исчезали и откуда-то появились. Обратимся к
единицам. 3 машины – это три единицы. 5 бидонов – это подразделение
каждой из трех единиц на соизмеримые с ними 5 единиц. |
|
| |
И при том от перестановки сомножителей результат, как
известно, не изменится. В этом смысле что такое дерево – это
способ упорядочивания элементов. Тогда, если мы переставляем
сомножители, то мы тем самым будем изменять и соотношение между
элементами. Чего мы не знаем, скажем? – мы не знаем общего количества
молока. Мы имеем множество связок: бидон и его ёмкость в литрах, машину
и её ёмкость в бидонах. Еще что-то, скажем, склада, и его ёмкость в
машинах, и т.д. Т.о., относительно одного объекта мы имеем, с одной
стороны, ёмкость каждого из объектов, и с другой стороны, количество
объектов. Т.о. мы имеем связки между единицами, такие, что всякая
единица верхнего уровня оказывается в то же самое время содержащей
единицы нижнего уровня. В таком случае как мы можем рассматривать
умножение слева направо, например, 3*5*18. Его мы можем рассматривать
таким образом, что 3 – это количество единиц верхнего уровня, 5 – что
каждая из единиц верхнего уровня n содержит по пять единиц уровня n-1, в
свою очередь каждая единица уровня n-1 содержит по 18 единиц уровня n-2.
При этом все элементы дерева, за исключением нижнего, представляют собой
контейнеры. В чем заключается основное правило? Оно заключается в
эквивалентности, равенстве контейнера как отдельно взятой единицы и
числа элементов, или ёмкости этого контейнера. То есть это как бы одно и
то же. Отсюда в качестве следствия мы получаем множество единиц и
множество субъединиц, и это отношение мы можем перевернуть таким
образом, что единицы мы будем рассматривать как субъединицы, а
субъединицы как единицы, и при этом конечный результат не изменится. То
есть если у нас есть 5 бидонов с ёмкостью по 18 литров, то если мы
перевернем эти отношения, то получим, что один литр у нас будет равен 5
бидонам, и тогда 18 литров будет равно 90 бидонам. Но очевидно, что в
этом случае отношения извращаются. Однако при этом мы получаем множество
эквивалентных деревьев. Например, если у нас есть дерево 3,5,18, то у
нас будут также эквивалентные им деревья 3,18,5; 5,18,3 и т.д. Но при
этом у нас будут уже совершенно другого рода отношения между единицами и
их емкостями. |
|
| |
Выражение 3,5,18 подразумевает три одинаковых
дерева, 5,18, 3 подразумевает 5 одинаковых деревьев. |
|
| |
Например, ящик спичек. В каждом ящике 40 упаковок
спичек, в каждой упаковке – 10 коробков спичек, в каждом коробке – по 50
спичек. Тогда ящик даст вершину n дерева. n-1 уровень = 40 упаковкам,
n-2 уровень содержит 10 коробков спичек, n-3 уровень содержит по 50
спичек в коробке. 66. Например, ящик спичек. В каждом ящике 40 упаковок
спичек, в каждой упаковке – 10 коробков спичек, в каждом коробке – по 50
спичек. Тогда ящик даст вершину n дерева. n-1 уровень = 40 упаковкам,
n-2 уровень содержит 10 коробков спичек, n-3 уровень содержит по 50
спичек в коробке.
|
|
| |
Итак, мы получили выражения: 50 спичек в коробке, 10 коробков в
упаковке, 40 упаковок в ящике. Какое-то количество в чем-то. 60 км в час
=60 километров в часе, то есть 60 километров находится в часе. Но ведь
это – отношение множества единиц расстояния ко времени. То есть мы пишем
60км/час, 50руб/кг ветчины. То есть определенное количество ветчины – 1
кг, равно 50 рублям. С другой стороны, 20 г /руб – 20 грамм ветчины
содержится в одном рубле. То есть что в лоб, что по лбу, либо одно
содержится в единице другого, либо другое содержится в единице первого.
То есть одно берется по отношению к другому, и именно, к единице
другого. При этом если в единице а содержится б единиц с, то 1а=бс, то
с=а/б. |
|
| |
Мы можем поменять сомножители местами и
сказать, что каждая спичка содержит 50 коробок, каждая коробка содержит
10 упаковок, каждая упаковка содержит 40 ящиков. результате от этого не
изменится. Хотя мы можем поступить и иначе, сказав, что каждая спичка
равна 1/50 коробки и т.д. |
|
| |
Разумеется, возможна и другая операция. Если мы
имеем 20000спичек, то мы можем это множество разделить на 50, и получим
400 коробок. 400 коробок можем разделить на 10, получим 40 упаковок,
которые разместим в одном ящике. |
|
| |
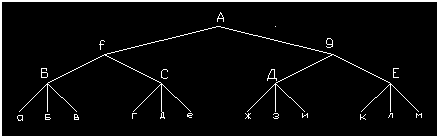 При рассмотрении единиц нужно учитывать еще 1 момент.
Например, если есть множество городов (см. рис.) , которые упорядочены
между собой, и совершается поездка по ним, то можно среди них выделить
подмножество городов, например, если множество упорядоченных городов
есть абвгде…., то в результате деления на подмножества получим, к
примеру, абв, где, …., в свою очередь, из подмножеств можем образовать
множества, их объединяющие, и всё это закончить одним множеством. Т.о.
получим дерево При рассмотрении единиц нужно учитывать еще 1 момент.
Например, если есть множество городов (см. рис.) , которые упорядочены
между собой, и совершается поездка по ним, то можно среди них выделить
подмножество городов, например, если множество упорядоченных городов
есть абвгде…., то в результате деления на подмножества получим, к
примеру, абв, где, …., в свою очередь, из подмножеств можем образовать
множества, их объединяющие, и всё это закончить одним множеством. Т.о.
получим дерево
И вот здесь, когда мы говорим о
единицах, нужно иметь ввиду две вещи: единицу как процесс её выполнения,
и единицу как результат выполненного процесса. Если мы имеем систему
координат со значениями 0, 1, 2,…, то 1 – это результат процесса
выполнения движения от ноля до единицы, тогда как все промежуточные
значения между 0 и 1 могут рассматриваться как промежуточные значения
единицы, что соответствует, слева от них выполненной части единицы, и
справа - той, которая еще не выполнена, то есть, соответственно,
позитиву и негативу, если целью является выполнение единицы, и негативу
и позитиву, если целью является её невыполнение.
Соответственно, если мы едем из города а в город м, то поездку мы
условно разделяем на части, например, так, как это показано на рис.
Двигаясь от а к б, мы реализуем единицу аб, оказавшись в б, мы
реализовали единицу аб и приступаем к реализации единицы бв и т.д. |
|
| |
Но возвращаемся к нашим баранам. Мы брали объекты одного рода -
множество бидонов. Затем брали объекты другого рода - молоко, измеряемое
в литрах. Умножали бидоны на молоко, и в результате этого получали
молоко. Куда же делись бидоны? Что такое бидон?- это объект. Что такое
множество бидонов? - это множество объектов определенного рода. То есть
множество бидонов - это множество единиц какого-то рода.
|
|
| |
Что такое отношение принадлежности применительно к понятию объекта?
- это отношение принадлежности признака объекту. Признак объекта не
существует вне и независимо от своего носителя, объекта, и в этом смысле
признак есть вещь столь же виртуальная, поскольку рассматривается сам по
себе, сколько и реальная, поскольку рассматривается в качестве признака
объекта |
|
| |
Емкость бидона равна 18 литрам. Ёмкость бидона - это его свойство,
которое само по себе, вне и независимо от бидона, не существует, и она
может быть различна.
Ёмкость бидона - это не то, что существует вне бидона. Значит, мы
можем сказать, что 1 бидону соответствует ёмкость в 18 литров, и
записать: 18 литров/1 бидоне. Тогда, если у нас пять бидонов, то
получаем: 18л/бид*5бид=90 л, и молоко тут само по себе вообще не причем,
если не считать того обстоятельства, что молоко измеряется в тех же
самых единицах, что и ёмкость бидона. |
|
| |
Что такое бидон? - это контейнер. Что такое контейнер? - это вещь,
предназначение которой заключается в том, чтобы содержать в себе другие
вещи.
Молоко - это не контейнер, поскольку оно не содержит в
себе ничего, кроме себя.
Следовательно, в понятии контейнера заключается условие
реализации отношения принадлежности. Между молоком в бидоне и бидоном
выполняется отношение принадлежности: молоко принадлежит бидону. Помещик
выступает в качестве контейнера по отношению к крепостному крестьянину,
а родитель - в качестве контейнера по отношению к своему ребенку и т.п.. |
|
| |
Но в любом случае контейнер сам по себе не имеет смысла. Не имел бы
смысла бидон, если бы он не предназначался для перемещения жидкостей.
Чтобы существовал контейнер в качестве объекта, нужно, чтобы
существовало нечто, что могло бы ограничиваться контейнером, то есть
нечто, которое нужно ограничивать. Отношение принадлежности всегда имеет
ввиду отношение между объектами, одна сторона противоположности
предполагает другую и определяется другой. Контейнер есть производная,
или вещь
произведенная относительно другой вещи, и он определяется
свойствами этой другой вещи. Для того, чтобы явился миру крепостной
крестьянин, необходимо, чтобы существовал крестьянин, по отношению к
которому был создан контейнер в виде дворянско-помещичьего государства,
о.о. ограничивающего его свободу. Вы способны к многообразной
деятельности. Но вы работаете в какой-то организации и выполняете в ней
определенную работу. Организация в той мере, в какой ограничивает и
определяет формы вашей деятельности выступает по отношению к вам в
качестве контейнера. Мы не свободны в той мере, в какой оказываемся
зависимы от того множества контейнеров, принадлежностью которых мы
являемся. |
|
| |
26.02.11 г. |
|
 При рассмотрении единиц нужно учитывать еще 1 момент.
Например, если есть множество городов (см. рис.) , которые упорядочены
между собой, и совершается поездка по ним, то можно среди них выделить
подмножество городов, например, если множество упорядоченных городов
есть абвгде…., то в результате деления на подмножества получим, к
примеру, абв, где, …., в свою очередь, из подмножеств можем образовать
множества, их объединяющие, и всё это закончить одним множеством. Т.о.
получим дерево
При рассмотрении единиц нужно учитывать еще 1 момент.
Например, если есть множество городов (см. рис.) , которые упорядочены
между собой, и совершается поездка по ним, то можно среди них выделить
подмножество городов, например, если множество упорядоченных городов
есть абвгде…., то в результате деления на подмножества получим, к
примеру, абв, где, …., в свою очередь, из подмножеств можем образовать
множества, их объединяющие, и всё это закончить одним множеством. Т.о.
получим дерево